Презентация на тему по математике на тему Равносильность неравенств. Квадратные неравенства (10 классы)

соединены знаком
>,

только числа, называются числовыми неравенствами.
Знаки >, < называются знаками строгих неравенств.
Также используются знаки нестрогих неравенств: ≥, ≤.

которых должны заключаться значения неизвестных величин, чтобы неравенство было

верным.

называются равносильными

неравенства в другую с противоположным знаком, не меняя при

этом знака неравенства.

Обе части неравенства можно разделить или умножить на одно и то же положительное число (знак неравенства останется тем же).

Обе части неравенства можно разделить или умножить на одно и то же отрицательное число, но при этом знак неравенства нужно изменить на противоположный.

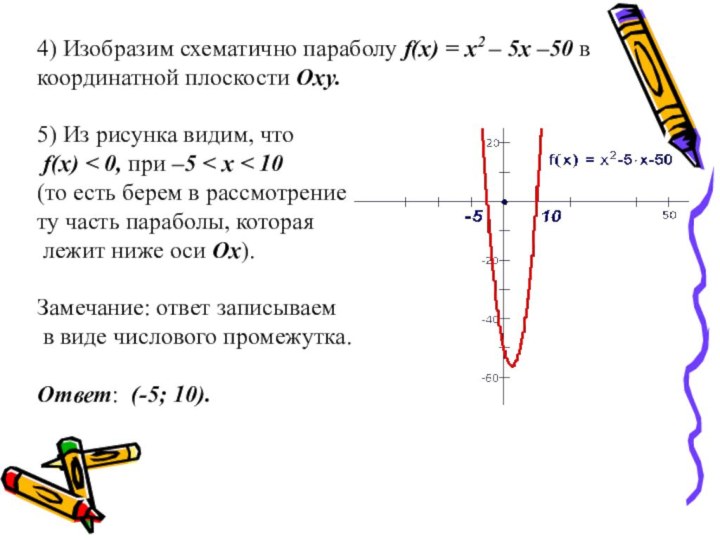
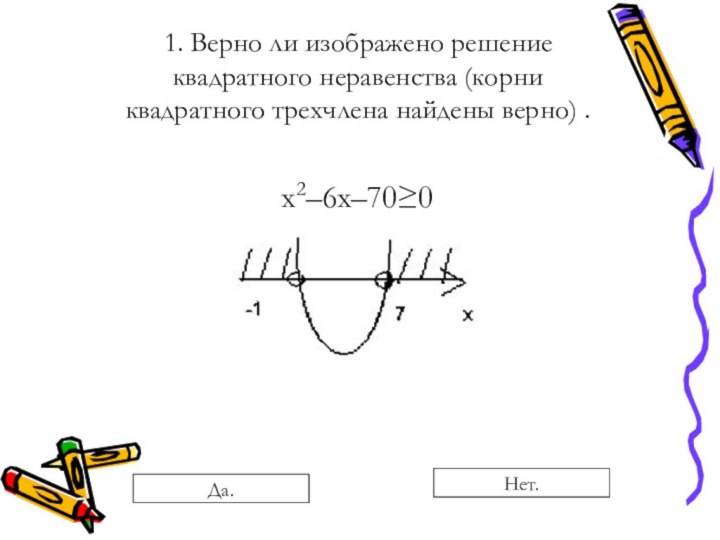
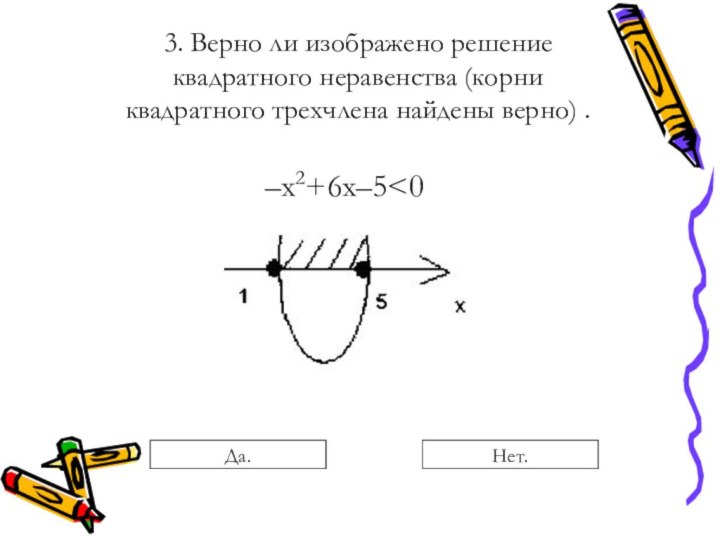
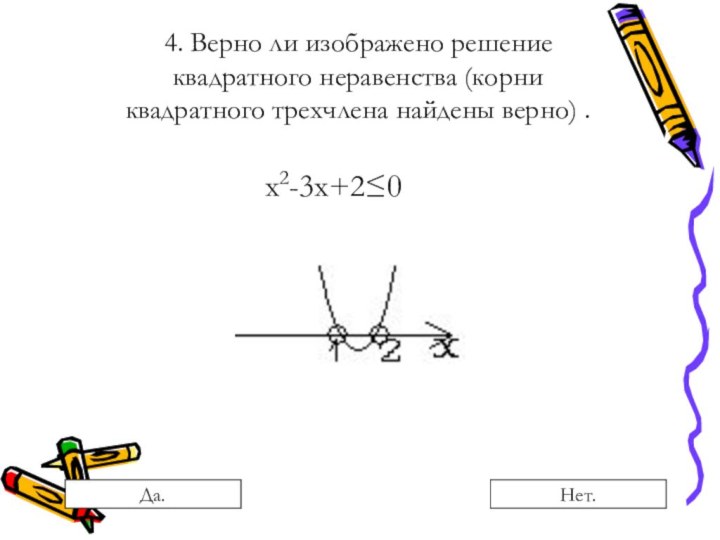
Преобразования, сохраняющие равносильность неравенств:

ax + b > 0 или ax + b

< 0,
где a и b – действительные числа и a ≠0.

a≠0, x- неизвестное. Тогда

неравенства вида f(x)>0, f(x)<0, f(x)≤0, f(x)≥0 называют квадратными неравенствами или неравенствами второй степени, причем первые два из этих неравенств называют строгими, другие - нестрогими

а≠0.
Квадратное уравнение может иметь один, два, или не иметь

вещественных корней.
Наличие корней определяется с помощью дискриминанта квадратного уравнения
D=b2-4ас.
Если D>0, то уравнение имеет два различных корня.
Если D=0, то уравнение имеет один корень.
Если D<0, то уравнение не имеет корней.
Находят корни (в случае их наличия) с помощью формулы корней квадратного уравнения.

все действительные числа, а неравенство ax2+bx+c0 не имеет решений;
Если

D=0, то решениями неравенства ax2+bx+c>0, являются все действительные значения x, кроме ,

а неравенство ax2+bx+c<0, не имеет решений;
Если D>0, то решениями неравенства ax2+bx+c>0 при a>0 являются все числа x такие, что xx2, где x1 и x2  - корни квадратного уравнения ax2+bx+c=0, т. е все значения x, лежащие вне отрезка [x1, x2]. 
Решениями неравенства ax2+bx+c<0 являются числа x такие, что x1т.е. все значения x из интервала (x1, x2).

5 x - 50 и
найдем такие значения x,

для которых f(x) < 0.

2) Графиком рассматриваемой функции является парабола,
ветви которой направлены вверх, так как a = 1, 1 > 0.

3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox), для этого решим квадратное уравнение
x2 – 5 x – 50 = 0.
x2 – 5 x – 50 = 0, a = 1, b = -5, c = -50.
D = b2 – 4ac;
D = (-5)2 –4*1*(-50) = 25 + 200 = 225 = 152, 225 > 0, значит уравнение имеет два действительных корня.
x1 = (-(-5) – 15) : 2 = -5;
x2 = (-(-5) + 15) : 2 = 10.
Нули функции: x = -5 и x = 10.

Метод рассмотрения квадратичной функции

5x –50 в
координатной плоскости Oxy.

5) Из рисунка видим,

что
f(x) < 0, при –5 < x < 10
(то есть берем в рассмотрение
ту часть параболы, которая
лежит ниже оси Ox).

Замечание: ответ записываем
в виде числового промежутка.

Ответ: (-5; 10).

выполнении задания Вам необходимо выбрать правильный вариант ответа.

Желаю

успеха!

квадратного трехчлена найдены верно) .
x2–6x–70≥0
Да.
Нет.

квадратного трехчлена найдены верно) .
3–х2≤х
Да.
Нет.

(корни квадратного трехчлена найдены верно) .
Да.
Нет.

квадратного трехчлена найдены верно) .
х2-3х+2≤0
Да.
Нет.