Слайд 2
Цели:
1) Образовательная: отработать и закрепить умения и
навыки решения квадратных уравнений.
2) Развивающая: развитие мыслительной деятельности, внимания;
развивать интерес к предмету; формировать потребность к приобретению знаний.
3) Воспитательная: воспитывать у учащихся трудолюбие, взаимоуважение; чувство ответственности, творчества.
Слайд 3
Эпиграф.
Посредством уравнений, теорем
Я уйму всяких разрешил проблем.
(Английский поэт средних веков -Чосер)
Слайд 6
2
Викторина. "Дальше, дальше..."
1. Сумма одночленов
2. Сотая часть числа
3.
Результат вычитания
4. Форма футбольного мяча
5. Наибольшее двухзначное число
6. Сколько
секунд в градусе
7. График линейной функции
8. Сколько нулей в записи числа миллиард
9. Какое число делится на все числа без остатка
10. Какое число не является ни простым, ни составным
11. Верное равенство двух отношений
Слайд 7
2
Викторина. "Дальше, дальше..."
12. Цель решения уравнения
13. Зависимость одной
переменной от другой
14. На сколько надо разделить 3, чтобы
получить 6
15. Сколько минут в трёх пятых часа
16. Деление числителя и знаменателя на одно и то же число
17. Сколько получится десятков, если 2 десятка умножить на
2 десятка
18. Корень уравнения |x|= -7
19. Число, одна треть которого составляет 12
20. Название свойства сложения (a+b)+c=a+(b+c)
21. Независимая переменная
Слайд 9
Квадратные уравнения — это фундамент, на котором покоится величественное
здание математики. Они находят широкое применение при решении различных
тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств, большого количества разных типов задач.
Слайд 10
При каком условии полное квадратное уравнение не имеет
действительных корней?
а) D=0
б)D 0 в)D 0
2. При каком условии полное квадратное уравнение имеет 1 действительный корень?
а) D=0 б) D 0 в)D 0
3. При каком условии полное квадратное уравнение имеет 2 действительных корня?
а) D=0 б) D 0 в) D 0
4. Название выражения -4ac :
а ) уравнение б) корень в) дискриминант
5. Как называется квадратное уравнение, в котором b или c равны 0?
а) полное б)приведённое в) неполное
6.Математик, доказавший, что + = - p, * = q :
а) Декарт б) Пифагор в) Виет
Слайд 11
Проверка теста:
1)б 2)а 3)в
4)в 5)в 6)в
Слайд 12
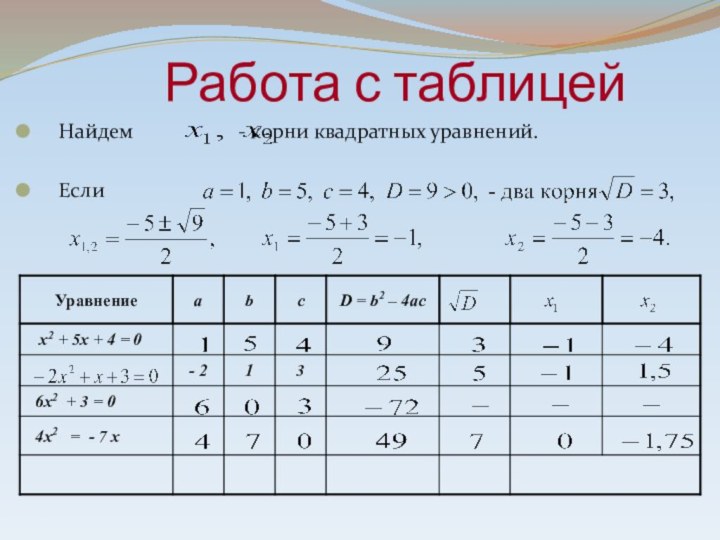
Работа с таблицей
Найдем
- корни квадратных
уравнений.
Если
Слайд 13
Работа с таблицей
Найдем
- корни квадратных
уравнений.
Если
Слайд 17
Перед началом экзамена. Преподаватель:
– Вы не волнуйтесь, положительную
оценку все получат.
Студент:
– А положительная – это какая?
Преподаватель:
– Больше
нуля!
Слайд 20
Квадратные уравнения
(триггер)
Жми сюда
Слайд 21
«Приобретать знания – это
храбрость.
Приумножать знания – это
мудрость.
А умело применять –
великое искусство»
Слайд 22
Издавна люди называют математику царицей наук, потому что
математика применяется в различных областях знаний. Один из важных
разделов математики – арифметика. Попробуйте решить простые арифметические задачи.
Слайд 23
7
Верно
5
Подумай
ещё!
Горело семь электрических лампочек. Две погасли. Сколько
осталось?
Слайд 24
1
Верно
24
Подумай
ещё!
Летела стая — 25 гусей. Одного убили.
Сколько осталось?
Слайд 25
3
Верно
10
Подумай
ещё!
Летели утки: одна впереди и две позади,
одна позади и две впереди, одна между двумя и
три в ряд. Сколько всего летело уток?
Слайд 26
3
Верно
6
Подумай
ещё!
Две матери, две дочери и бабушка с
внучкой. Сколько их всего?
Слайд 27
7
Верно
14
Подумай
ещё!
У одного отца есть шестеро сыновей.
У
каждого сына одна сестра.
Сколько у отца детей?
Слайд 28
1
Верно
10
Подумай
ещё!
На грядке сидели 6 воробьев, к ним
прилетели еще 5. Кот подкрался и схватил одного воробья.
Сколько воробьев осталось на грядке?
Слайд 29
3
Верно
4
Подумай
ещё!
У Марины было целое яблоко, две половинки
и 4 четвертинки.
Сколько было у нее яблок?
Слайд 30
1
Верно
3
Подумай
ещё!
Два сына и два отца съели 3
яйца. Сколько яиц съел каждый?
Слайд 31
5
Верно
3
Подумай
ещё!
На складе было 5 цистерн с горючим,
по 6 тонн в каждой. Из двух цистерн горючее
выдали. Сколько цистерн осталось?
Слайд 32
20
Верно
10
Подумай
ещё!
Пара лошадей пробежала 20 км. Сколько километров
пробежала каждая лошадь?
Слайд 33
Вывод:
«Человеку, изучающему алгебру, часто полезнее решить одну
и ту же задачу тремя различными способами, чем решить
три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
У. Сойер