- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к открытому уроку-проекту по алгебре в 7-8-9 классах История развития решения квадратных уравнений ГБОУ СШ №4, г.Байконур
Содержание
- 2. Древний Египет
- 4. Древний Вавилон
- 9. Древняя Греция
- 10. ДИОФАНТДревнегреческий математик, живший предположительно в III веке
- 14. ДРЕВНЯЯ ИНДИЯ
- 16. Приведем одну из задач знаменитого индийского математика
- 19. СРЕДНЕВЕКОВЫЙ ВОСТОК
- 21. «АЛЬ-ДЖЕБР» – ВОССТАНОВЛЕНИЕМ - АЛЬ-ХОРЕЗМИ НАЗЫВАЛ ОПЕРАЦИЮ
- 23. Задача. Квадрат и число 21 равны 10
- 25. Фибоначчи родился в
- 26. Знаменитый немецкий математик, протестантский пастор. В 1544
- 33. У. Соейр говорил : «Человеку, изучающему алгебру,
- 34. Скачать презентацию
- 35. Похожие презентации
Древний Египет



























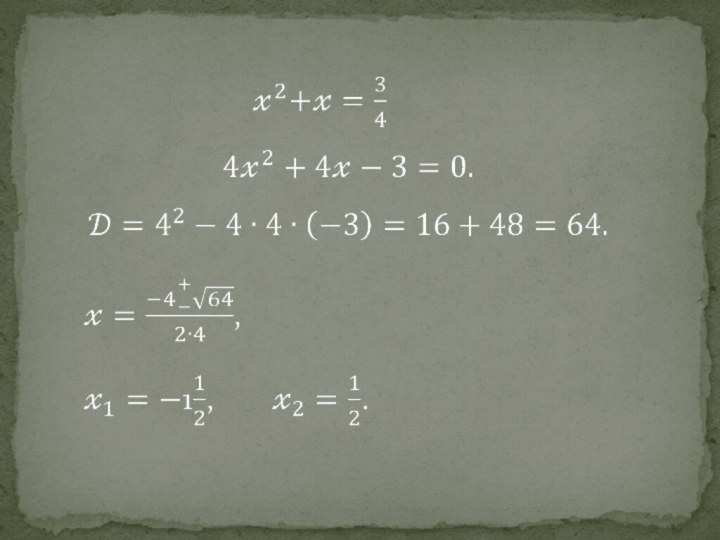
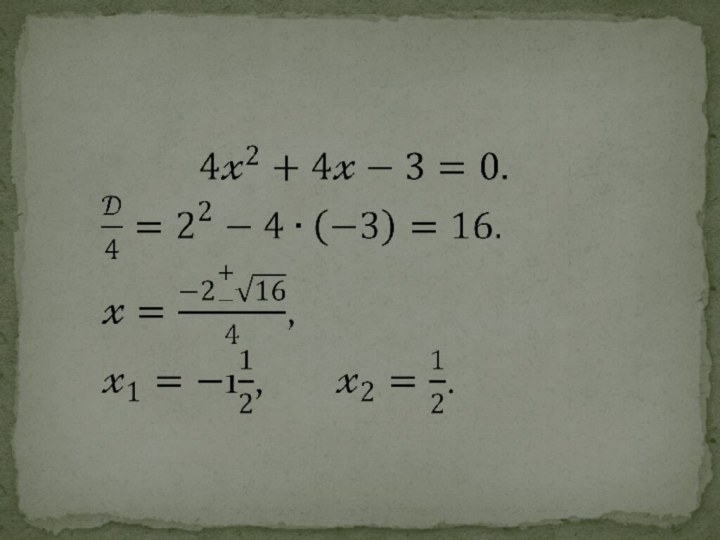
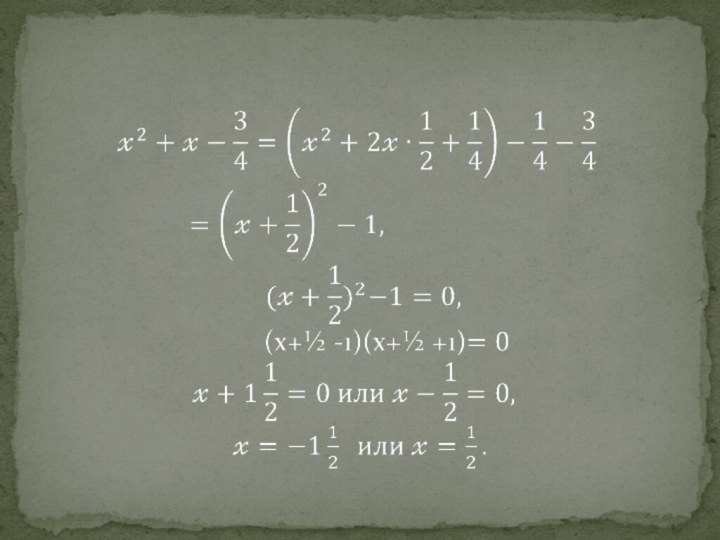

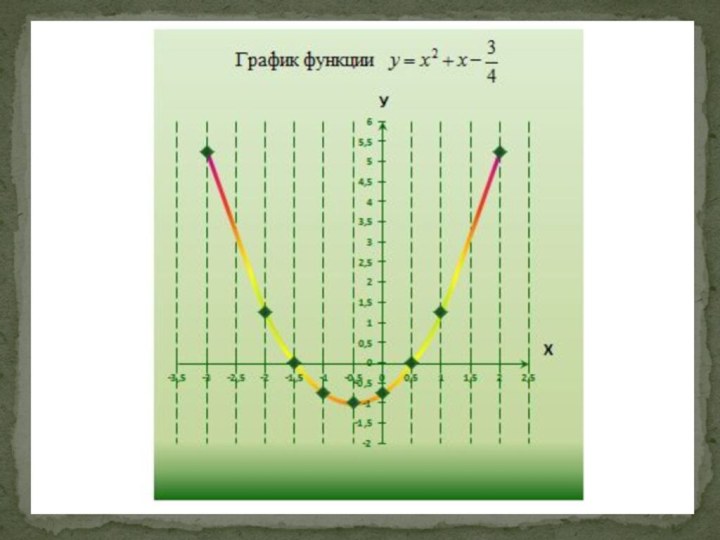


Слайд 10
ДИОФАНТ
Древнегреческий математик, живший предположительно в III веке до
н. э. Автор «Арифметики» — книги, посвящённой решению алгебраических уравнений.
время под «диофантовыми уравнениями» обычно понимают уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел. Диофант также одним из первых развивал математические обозначения.
Слайд 16
Приведем одну из задач знаменитого
индийского математика XII
века Бхаскары:
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их
в квадрате часть восьмая На поляне забавлялась.
А двенадцать по лианам…
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?
Слайд 21 «АЛЬ-ДЖЕБР» – ВОССТАНОВЛЕНИЕМ - АЛЬ-ХОРЕЗМИ НАЗЫВАЛ ОПЕРАЦИЮ ИСКЛЮЧЕНИЯ
ИЗ ОБЕИХ ЧАСТЕЙ УРАВНЕНИЯ ОТРИЦАТЕЛЬНЫХ ЧЛЕНОВ ПУТЕМ ДОБАВЛЕНИЯ РАВНЫХ
ЧЛЕНОВ, НО ПРОТИВОПОЛОЖНЫХ ПО ЗНАКУ.«АЛЬ-МУКАБАЛА» – ПРОТИВОПОСТАВЛЕНИЕ – СОКРАЩЕНИЕ В ЧАСТЯХ УРАВНЕНИЯ ОДИНАКОВЫХ ЧЛЕНОВ.
ПРАВИЛО «АЛЬ-ДЖЕБР»
ПРИ РЕШЕНИИ УРАВНЕНИЯ
ЕСЛИ В ЧАСТИ ОДНОЙ,
БЕЗРАЗЛИЧНО КАКОЙ,
ВСТРЕТИТСЯ ЧЛЕН ОТРИЦАТЕЛЬНЫЙ,
МЫ К ОБЕИМ ЧАСТЯМ
РАВНЫЙ ЧЛЕН ПРИДАДИМ,
ТОЛЬКО С ЗНАКОМ ДРУГИМ,
И НАЙДЕМ РЕЗУЛЬТАТ ПОЛОЖИТЕЛЬНЫЙ.
Слайд 23 Задача. Квадрат и число 21 равны 10 корням.
Найти корень.
Решение. Разделим пополам число корней – получишь
5, умножь 5 на само себя, от произведения отними 21, останется 4.
Извлеки корень из 4 – получишь 2.
Отними 2 от 5 – получишь 3, это и будет искомый корень. Или же прибавь к 5, что даст 7, это тоже есть корень.