вершину треугольника с серединой противоположной стороны
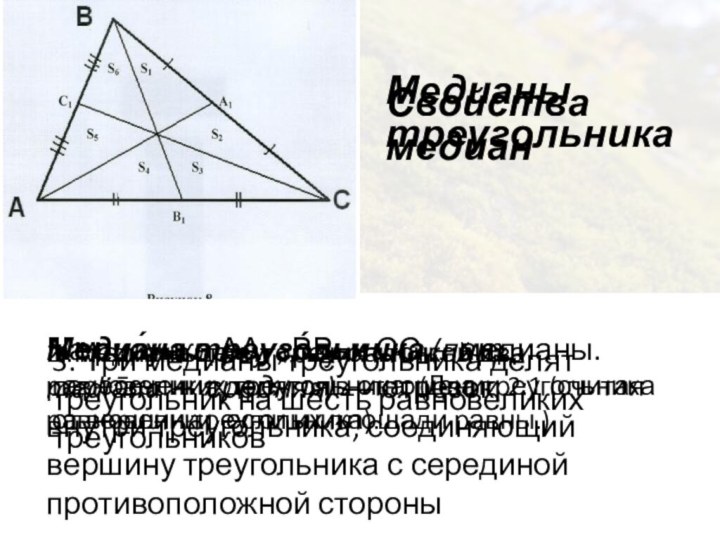
На рисунке АА₁ ,
ВВ₁ и СС₁ – медианы.Свойства медиан
1. Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершин треугольника).
2. Медиана делит треугольник на два равновеликих треугольника. (Два треугольника равновелики, если их площади равны.)
3. Три медианы треугольника делят треугольник на шесть равновеликих треугольников