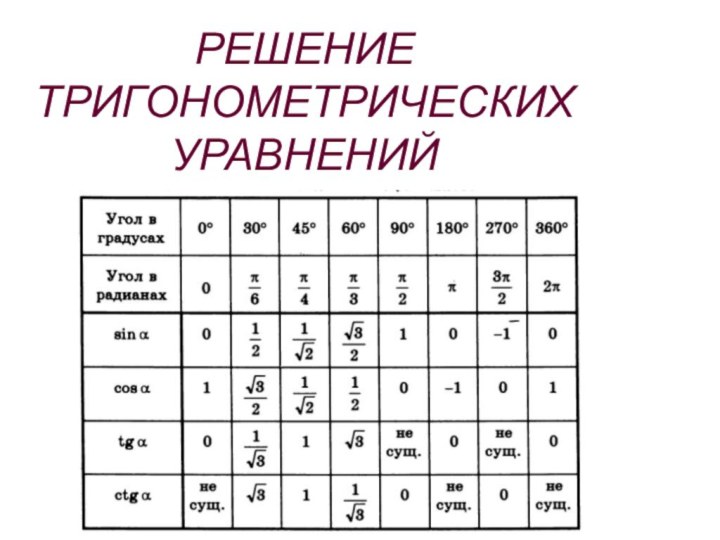
из [0;π], что
cos t = а.
Причём, | а
|≤ 1. arccos(- а) = π- arccos а
Примеры:
1)arccos(-1)
= π
2)arccos( )
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
![Решение тригонометрических уравнений Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos t](/img/tmb/6/586494/813bf4dca03246518ddea751786966d9-720x.jpg)











arccos(- а) = π- arccos а
Примеры:
1)arccos(-1)
= π
2)arccos( )
а
- а
arcsin(- а)= - arcsin а
Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.
arctg(-а) = - arctg а
-а
arctg(-а )
Примеры:
1) arctg√3/3 =
π/6
2) arctg(-1) =
-π/4
arcctg(- а) = π – arcctg а
- а
arcctg(- а)
1) arcctg(-1) =
Примеры:
3π/4
2) arcctg√3 =
π/6
2) cost=1
t = 2πk‚ kЄZ
3) cost = -1
t = π+2πk‚ kЄZ
2) sint=1
t = π/2+2πk‚ kЄZ
3) sint = - 1
t = - π/2+2πk‚ kЄZ
t = arcctg а + πk‚ kЄZ
Виды тригонометрических уравнений
Пример. Решите уравнение sinx + 2cosx = 0.
Решение: Разделим обе части уравнения на cosx.
Получим
Ответ:
Виды тригонометрических уравнений
П р и м е р . Решить уравнение: 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
tg2 x + 4 tg x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,
корни этого уравнения: y1 = −1, y2 = −3, отсюда
1) tg x = –1, 2) tg x = –3,
Ответ:
sin x + cos x = 1 .
Р е ш е н и е . Перенесём все члены уравнения
влево:
sin x + cos x – 1 = 0 ,