Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Производная (геометрический смысл)

Содержание

2. Цель:Решить задачу на нахождение уклона холма.Ввести новое
3. Решим задачу!В физике крутизна –отношение превышения местности к
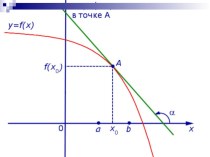
4. Чтобы вычислить уклон в определенной точке нужно
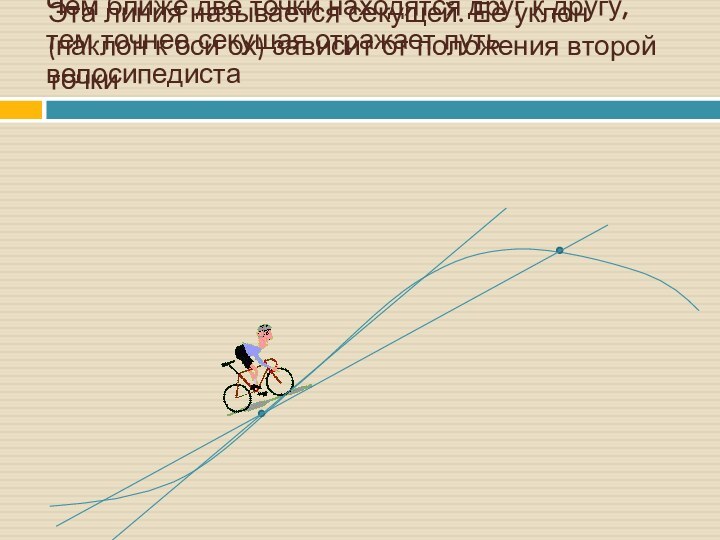
5. Эта линия называется секущей. Её уклон
6. Если первая и вторая точки совпадут, то
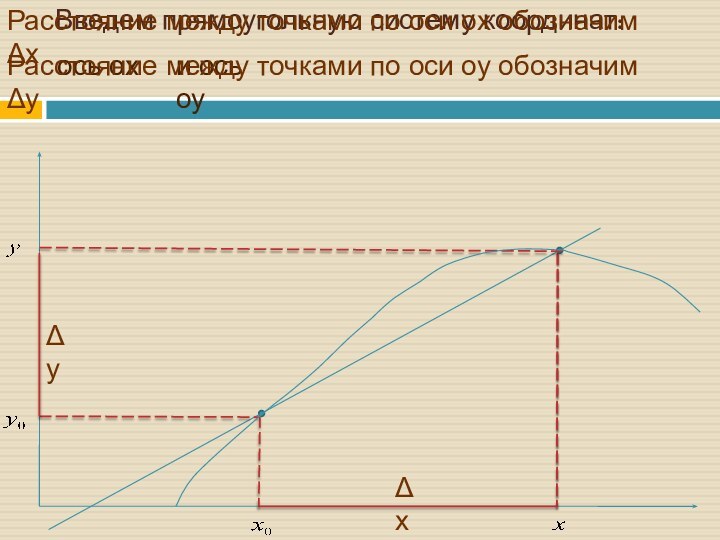
7. Введем прямоугольную систему координат: Расстояние между точками
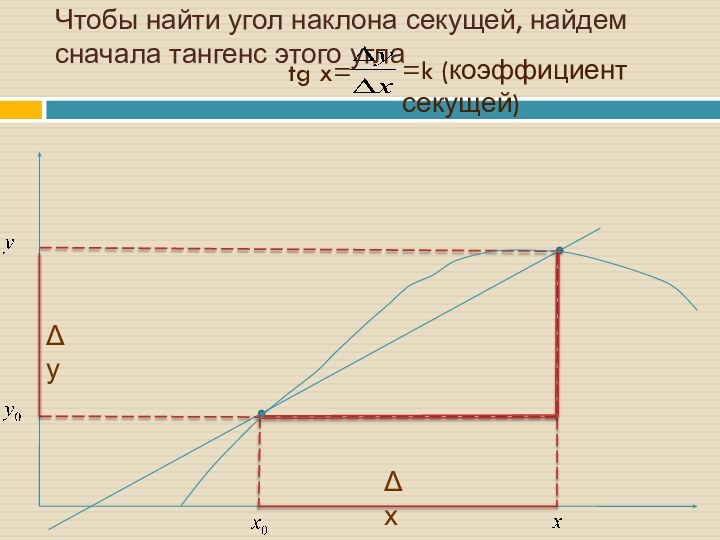
8. Чтобы найти угол наклона секущей, найдем сначала тангенс этого углаtg x= ΔуΔх=k (коэффициент секущей)
9. Если вторая точка приближается к первой, то
10. Когда отношение снижается
11. ОпределениеЕсли существует предел отношения
12. Геометрический смысл производнойсостоит в том, что производная
13. Зачем нужна производная? Производная может отображать
14. Зачем нужна производная?Производная это показатель изменения любой функции в любой момент и в любой точке.
15. Скачать презентацию
16. Похожие презентации

Цель:Решить задачу на нахождение уклона холма.Ввести новое понятие – производная.Определить, в чем состоит геометрический смысл производной.Определить, зачем нужна производная.

Главная
Алгебра
Производная (геометрический смысл)

Производная (геометрический смысл)Черень Римма Ивановна

Цель:Решить задачу на нахождение уклона холма.Ввести новое понятие – производная.Определить, в чем

Решим задачу!В физике крутизна –отношение превышения местности к горизонтальному протяжению, на котором оно наблюдается.

Чтобы вычислить уклон в определенной точке нужно взять другую точку на холме

Эта линия называется секущей. Её уклон (наклон к оси ох) зависит

Если первая и вторая точки совпадут, то прямая станет не секущей, а

Введем прямоугольную систему координат: Расстояние между точками по оси ох обозначим Δхось

Чтобы найти угол наклона секущей, найдем сначала тангенс этого углаtg x= ΔуΔх=k (коэффициент секущей)

Если вторая точка приближается к первой, то Δх→0Значит, при Δх→0 значение коэффициента

Когда отношение снижается до нуля, то его называют

ОпределениеЕсли существует предел отношения при Δх→0, то указанный

Геометрический смысл производнойсостоит в том, что производная выражает тангенс угла наклона касательной

Зачем нужна производная? Производная может отображать степень изменения всего, например:изменение уклона

Зачем нужна производная?Производная это показатель изменения любой функции в любой момент и в любой точке.

Велосипедист: http://ru.coolclips.com/media/?D=wb024394&Ref=CSb,2729Источники:

Слайды презентации

Слайд 2 Цель:
Решить задачу на нахождение уклона холма.
Ввести новое понятие

Цель:Решить задачу на нахождение уклона холма.Ввести новое понятие – производная.Определить, в

– производная.
Определить, в чем состоит геометрический смысл производной.
Определить, зачем

нужна производная.

Слайд 3 Решим задачу!
В физике крутизна –отношение превышения местности к горизонтальному

Решим задачу!В физике крутизна –отношение превышения местности к горизонтальному протяжению, на котором

протяжению, на котором оно наблюдается.

Это соотношение называется уклоном

Иными словами,

величина уклона равна тангенсу угла между поверхностью склона и горизонталью.

Как же вычислить уклон в определенной точке холма?

Слайд 4 Чтобы вычислить уклон в определенной точке нужно взять

Чтобы вычислить уклон в определенной точке нужно взять другую точку на

другую точку на холме и соединить их прямой линией.
Как

же вычислить уклон в определенной точке холма?

Слайд 5 Эта линия называется секущей. Её уклон (наклон к

оси ох) зависит от положения второй точки
Чем ближе две

точки находятся друг к другу, тем точнее секущая отражает путь велосипедиста

Слайд 6 Если первая и вторая точки совпадут, то прямая

Если первая и вторая точки совпадут, то прямая станет не секущей,

станет не секущей, а касательной.
Уклон касательной в первой точке

равен уклону холма в этой точке.

Слайд 7 Введем прямоугольную систему координат:
Расстояние между точками по оси

Введем прямоугольную систему координат: Расстояние между точками по оси ох обозначим

ох обозначим Δх
ось ох
и ось оу
Расстояние между точками по

оси оу обозначим Δу

Δх

Δу

Слайд 8 Чтобы найти угол наклона секущей, найдем сначала тангенс

этого угла
tg x=
Δу
Δх
=k (коэффициент секущей)

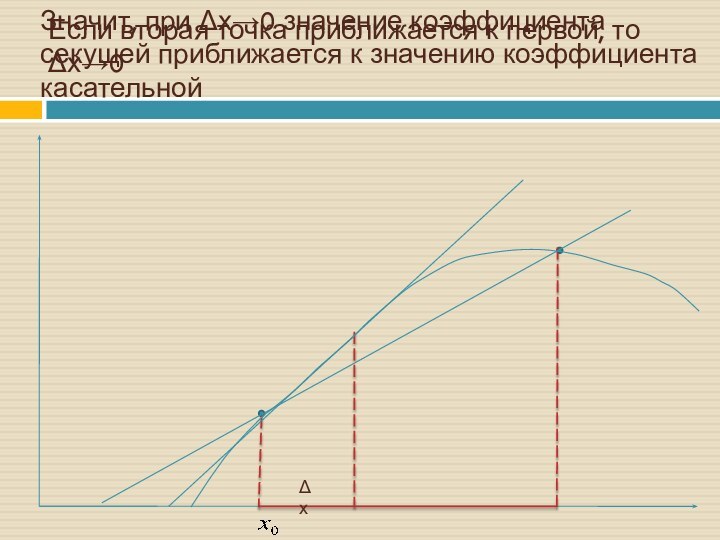
Слайд 9 Если вторая точка приближается к первой, то Δх→0
Значит,

Если вторая точка приближается к первой, то Δх→0Значит, при Δх→0 значение

при Δх→0 значение коэффициента секущей приближается к значению коэффициента

касательной

Δх

Слайд 10 Когда отношение снижается до

Когда отношение снижается до нуля, то его называют производной

нуля, то его называют производной и обозначают новым символом

Производная функции это уклон её касательной в каждой точке. Значит, чтобы найти уклон касательной нужно найти производную от функции, которая задает вид холма.

y=kx+b

Слайд 11 Определение
Если существует предел отношения

ОпределениеЕсли существует предел отношения при Δх→0, то указанный предел

при Δх→0, то указанный предел называют производной функции в

точке х.

Производная функции есть новая функция, «произведенная» из первой.

Слайд 12 Геометрический смысл производной
состоит в том, что производная выражает

Геометрический смысл производнойсостоит в том, что производная выражает тангенс угла наклона

тангенс угла наклона касательной в некоторой точке х ,

или угловой коэффициент касательной

Слайд 13 Зачем нужна производная?
Производная может отображать степень

изменения всего, например:
изменение уклона в зависимости от крутизны склона;
изменение

популяции дельфинов в зависимости от температуры воды;
изменение массы шарика в зависимости от его объема;
изменение цены пиццы в зависимости от её размеров;
изменение пройденного расстояния в зависимости от времени.