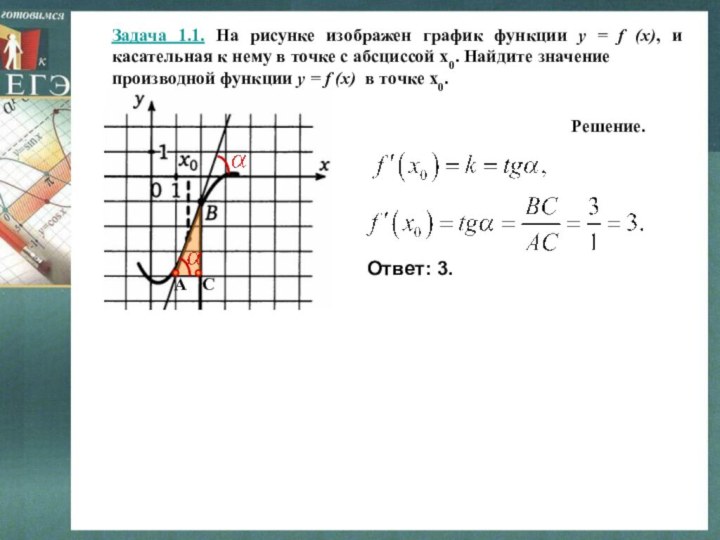
= f (x), и касательная к нему в точке
с абсциссой х0. Найдите значениепроизводной функции y = f (x) в точке х0.
Решение.
Ответ: 3.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




Решение.
Ответ: 3.
Теоретические сведения.
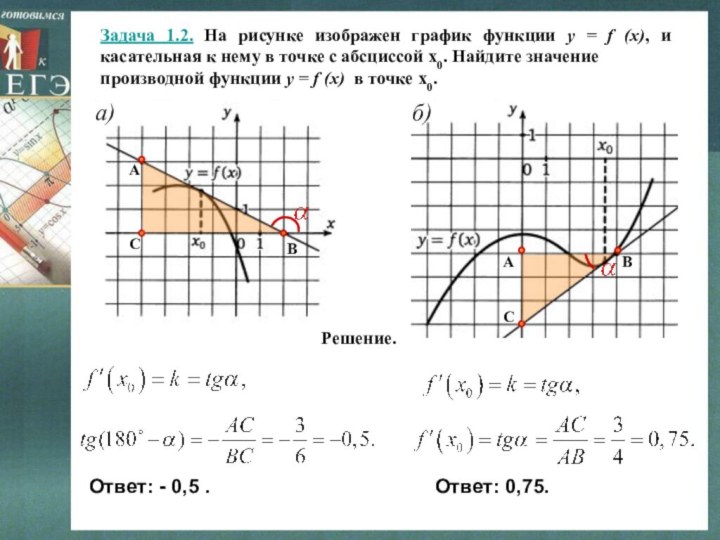
Решение.
Ответ: - 0,5 .
Ответ: 0,75.
С
В
А
a)
б)
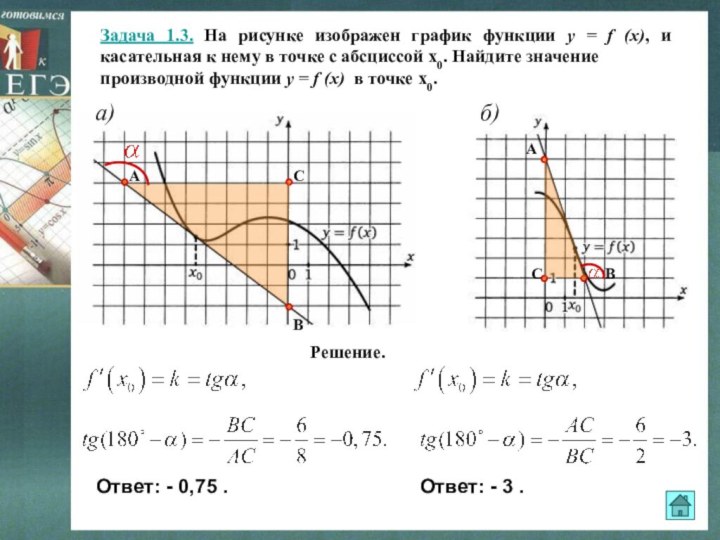
Решение.
Ответ: - 0,75 .
А
В
С
А
В
С
Ответ: - 3 .
a)
б)
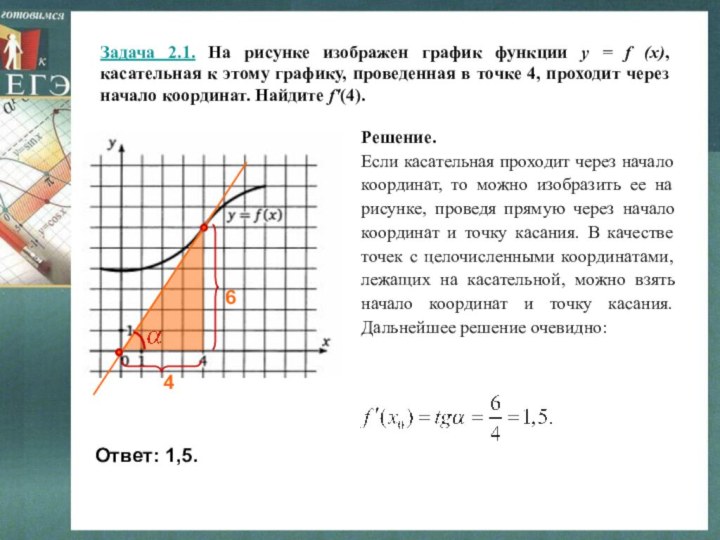
Решение.
Если касательная проходит через начало координат, то можно изобразить ее на рисунке, проведя прямую через начало координат и точку касания. В качестве точек с целочисленными координатами, лежащих на касательной, можно взять начало координат и точку касания. Дальнейшее решение очевидно:
Ответ: 1,5.
6
4
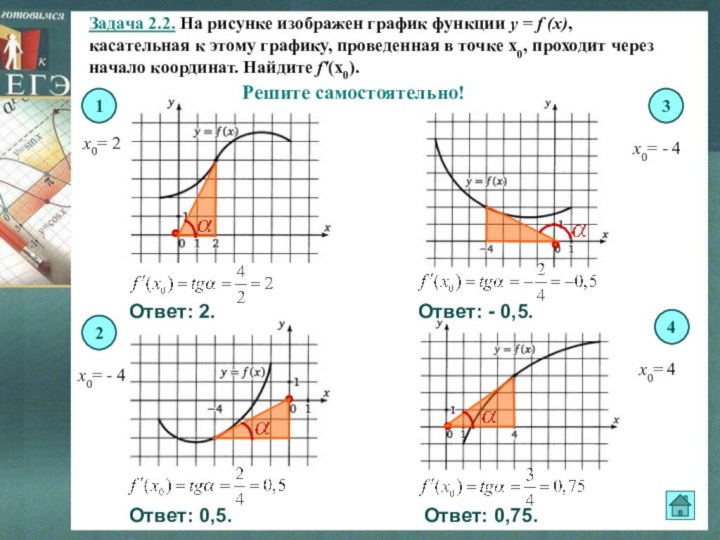
х0= 2
х0= - 4
х0= - 4
х0= 4
1
3
4
2
Решите самостоятельно!
Ответ: 2.
Ответ: 0,5.
Ответ: - 0,5.
Ответ: 0,75.
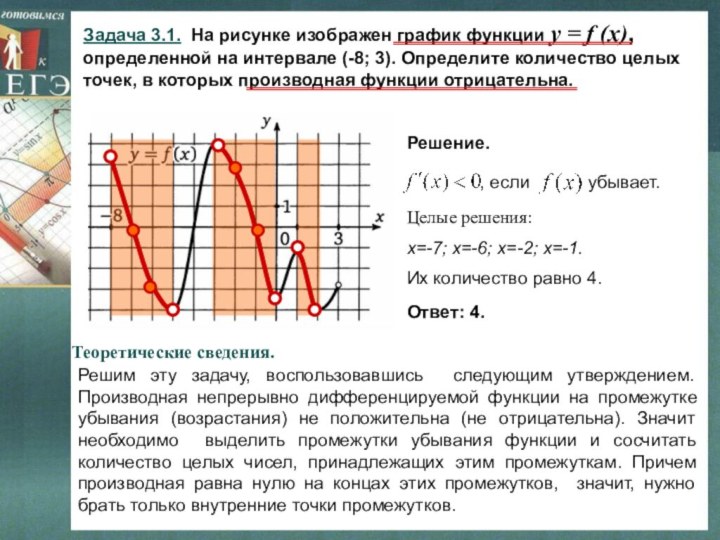
Решим эту задачу, воспользовавшись следующим утверждением. Производная непрерывно дифференцируемой функции на промежутке убывания (возрастания) не положительна (не отрицательна). Значит необходимо выделить промежутки убывания функции и сосчитать количество целых чисел, принадлежащих этим промежуткам. Причем производная равна нулю на концах этих промежутков, значит, нужно брать только внутренние точки промежутков.
Решение.
Целые решения:
х=-7; х=-6; х=-2; х=-1.
Их количество равно 4.
Ответ: 4.
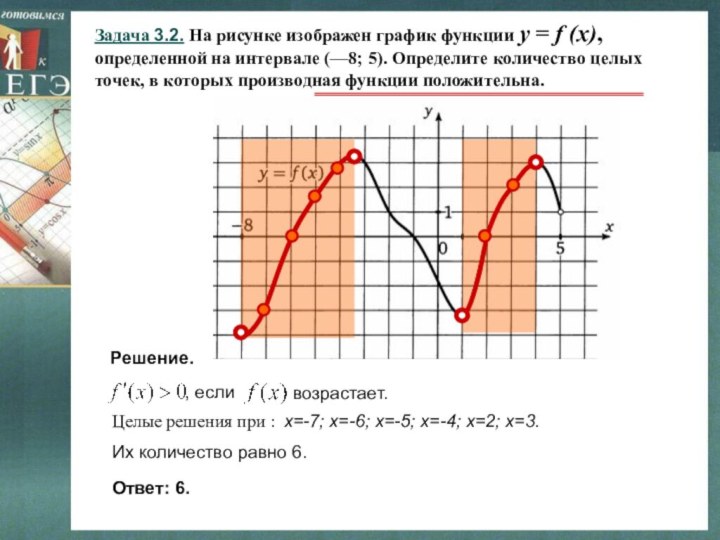
Теоретические сведения.
Решение.
Целые решения при : х=-7; х=-6; х=-5; х=-4; х=2; х=3.
Их количество равно 6.
Ответ: 6.
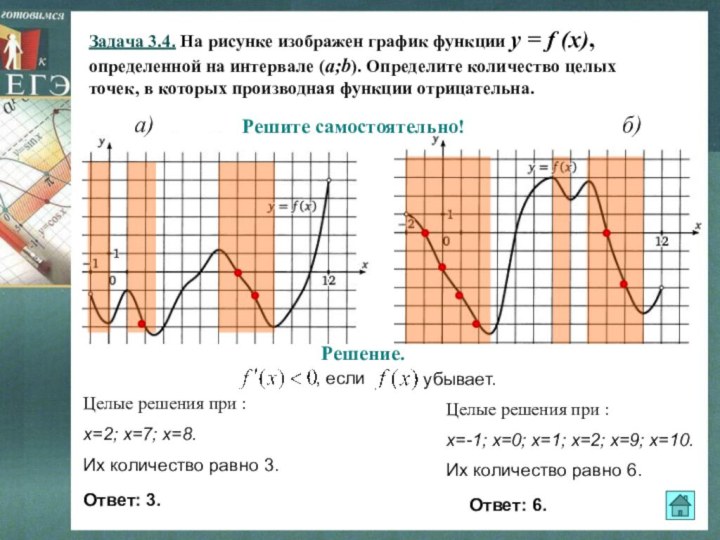
a)
б)
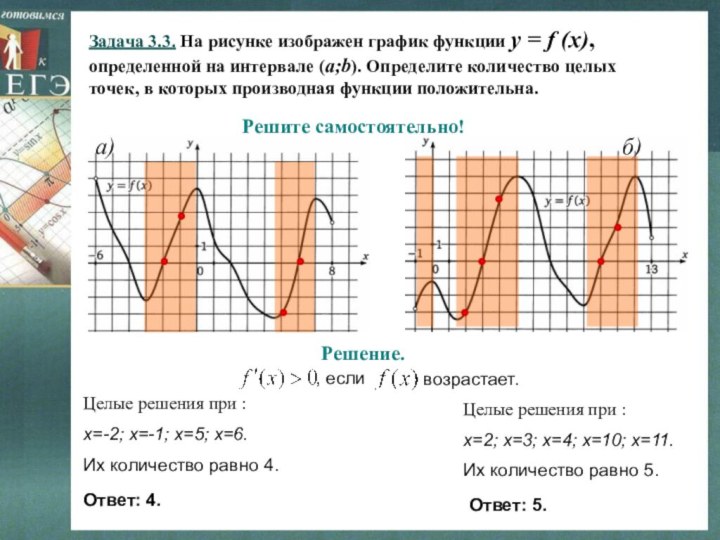
Решите самостоятельно!
Решение.
Целые решения при :
х=-2; х=-1; х=5; х=6.
Их количество равно 4.
Целые решения при :
х=2; х=3; х=4; х=10; х=11.
Их количество равно 5.
Ответ: 4.
Ответ: 5.
Решите самостоятельно!
a)
б)
Решение.
Целые решения при :
х=2; х=7; х=8.
Их количество равно 3.
Целые решения при :
х=-1; х=0; х=1; х=2; х=9; х=10.
Их количество равно 6.
Ответ: 3.
Ответ: 6.
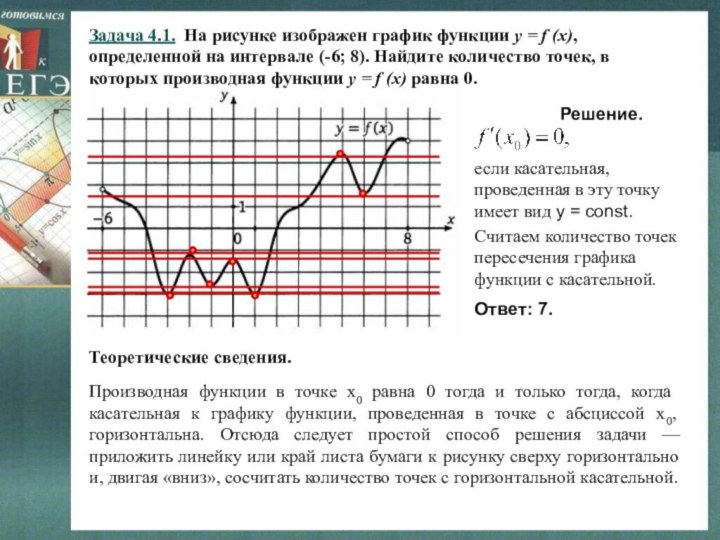
Задача 4.1. На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
Теоретические сведения.
Решение.
если касательная, проведенная в эту точку имеет вид у = const.
Считаем количество точек пересечения графика функции с касательной.
Ответ: 7.
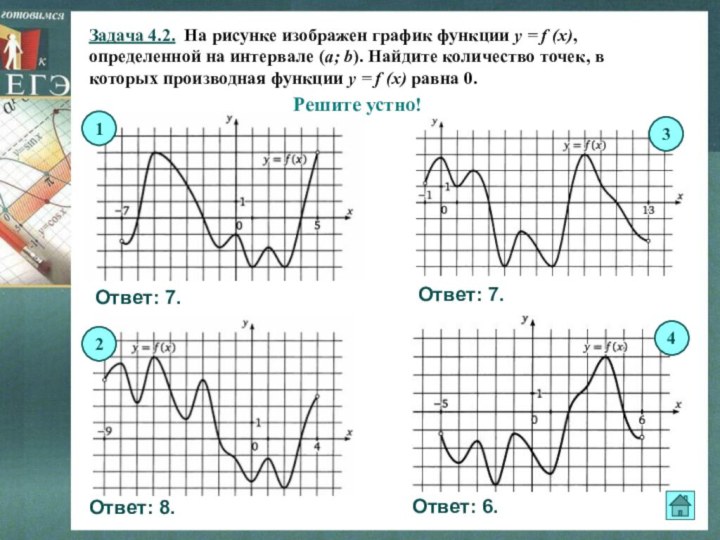
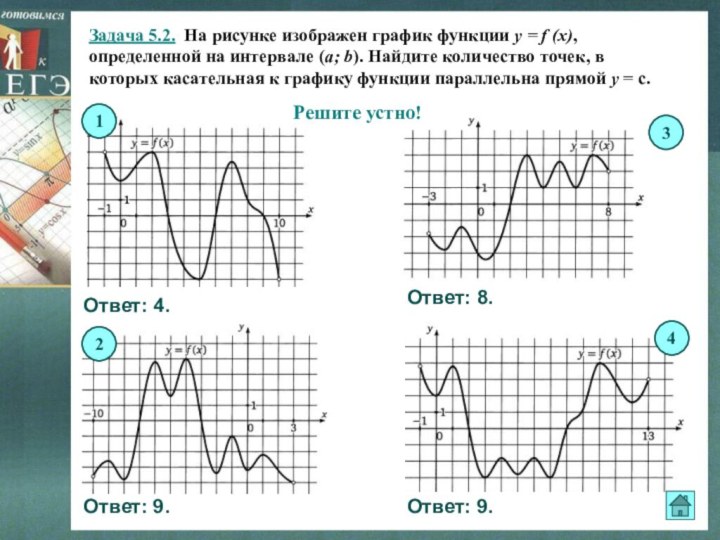
Решите устно!
Ответ: 7.
Ответ: 7.
Ответ: 8.
Ответ: 6.
1
3
4
2
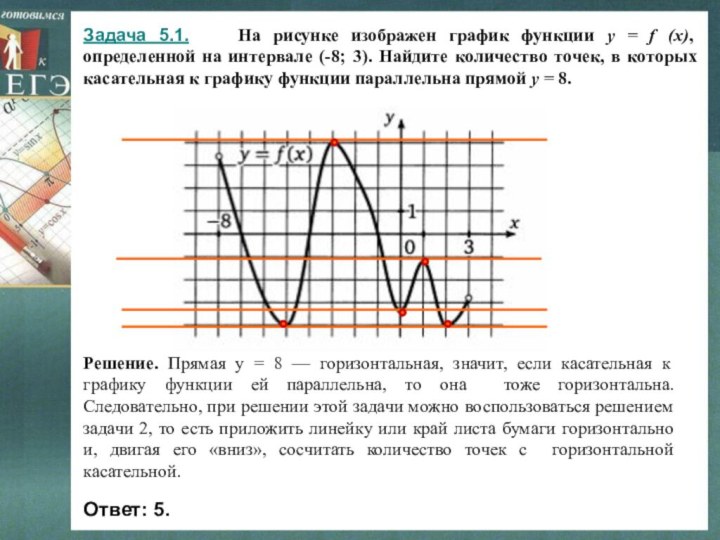
Решение. Прямая у = 8 — горизонтальная, значит, если касательная к графику функции ей параллельна, то она тоже горизонтальна. Следовательно, при решении этой задачи можно воспользоваться решением задачи 2, то есть приложить линейку или край листа бумаги горизонтально и, двигая его «вниз», сосчитать количество точек с горизонтальной касательной.
Ответ: 5.
1
3
4
2
Решите устно!
Ответ: 4.
Ответ: 9.
Ответ: 8.
Ответ: 9.
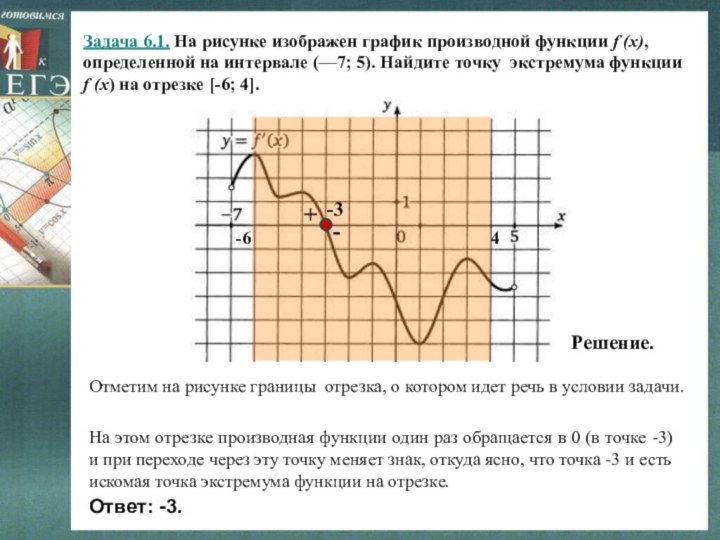
На этом отрезке производная функции один раз обращается в 0 (в точке -3) и при переходе через эту точку меняет знак, откуда ясно, что точка -3 и есть искомая точка экстремума функции на отрезке.
Решение.
Отметим на рисунке границы отрезка, о котором идет речь в условии задачи.
Ответ: -3.
-3
+
-
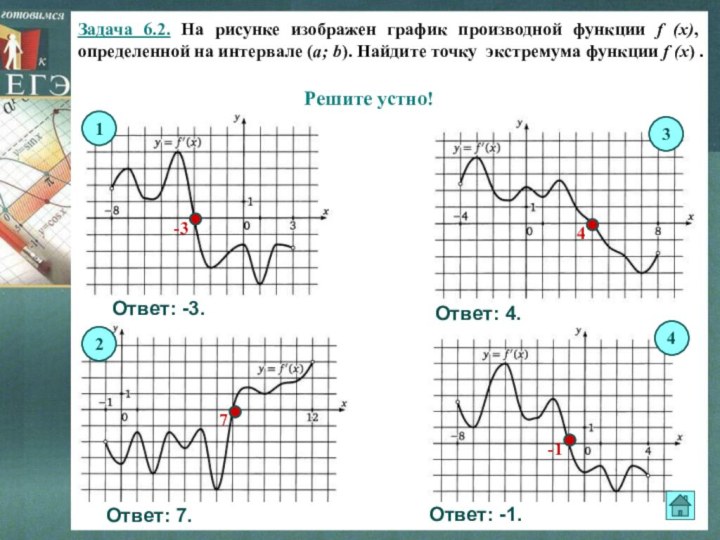
Решите устно!
1
3
4
2
Решение.
Ответ: 1 .
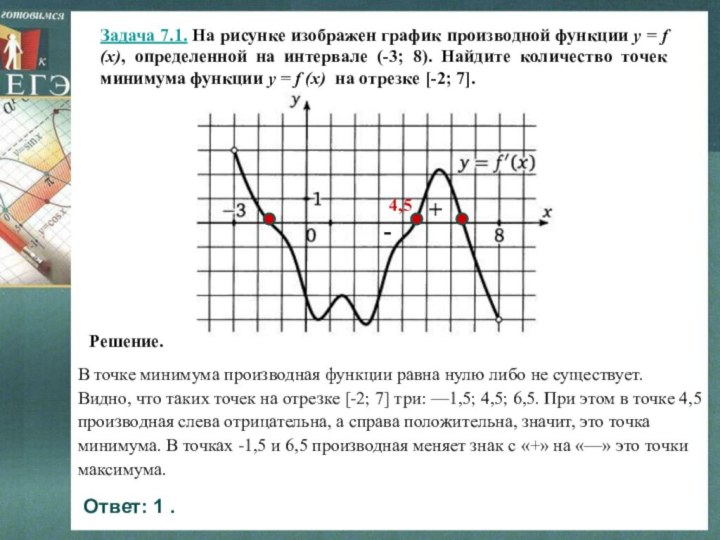
4,5
-
+
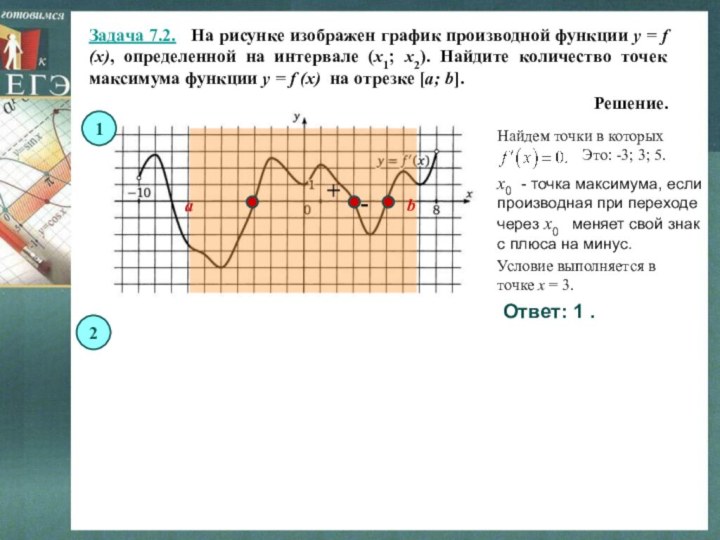
Задача 7.1. На рисунке изображен график производной функции y = f (x), определенной на интервале (-3; 8). Найдите количество точек минимума функции y = f (x) на отрезке [-2; 7].
Решение.
Ответ: 1 .
Ответ: 3 .
a
b
a
b
x0 - точка максимума, если производная при переходе через x0 меняет свой знак с плюса на минус.
-
+
Условие выполняется в точке x = 3.
Решение.
Условие выполняется в точках: -1; 8; 13.
1
Решение аналогично.
2
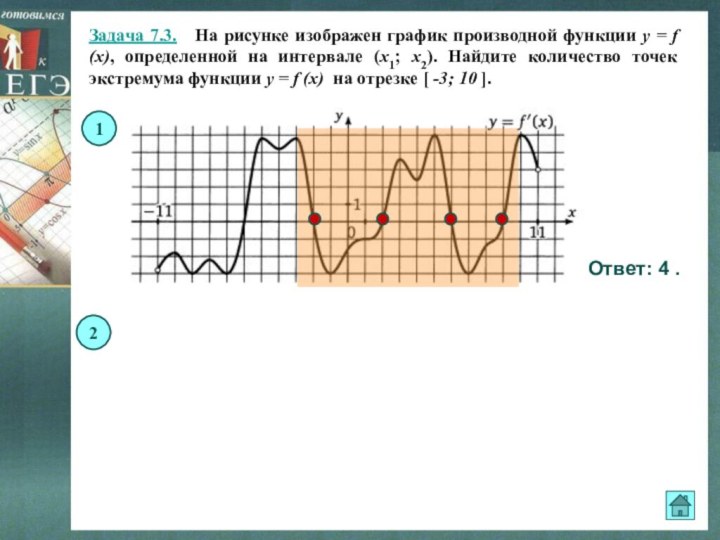
Ответ: 4 .
Ответ: 4 .
1
2
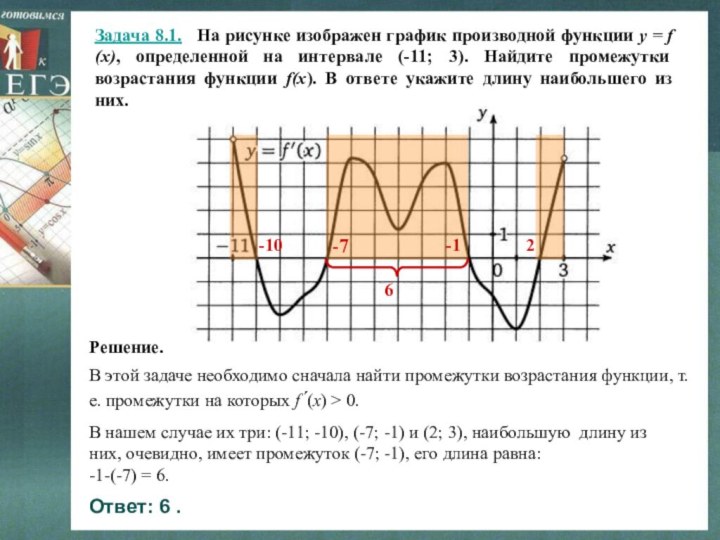
В этой задаче необходимо сначала найти промежутки возрастания функции, т.е. промежутки на которых f´(x) > 0.
Решение.
В нашем случае их три: (-11; -10), (-7; -1) и (2; 3), наибольшую длину из них, очевидно, имеет промежуток (-7; -1), его длина равна:
-1-(-7) = 6.
Ответ: 6 .
-10
-7
-1
2
6
1
Решение.
Решение.
Ответ: 6 .
Ответ: 3 .
Найдем промежутки убывания функции, т.е. промежутки на которых f´(x) < 0.
Наибольшую длину из них имеет промежуток (-10; -4)
-10
-4
Решение аналогично: ищем промежутки на которых f´(x) < 0.
Наибольший из них имеет длину равную 3.
6
3
2
3
Решение.
Решение.
Ответ: 1 .
Ответ: 2 .
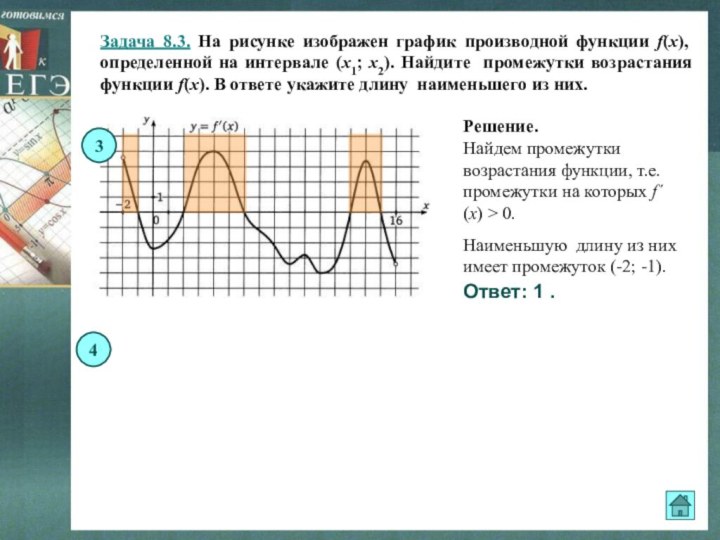
Найдем промежутки возрастания функции, т.е. промежутки на которых f´(x) > 0.
Наименьшую длину из них имеет промежуток (-2; -1).
Решение аналогично: ищем промежутки на которых f´(x) > 0.
Наименьший из них имеет длину равную 2.
4
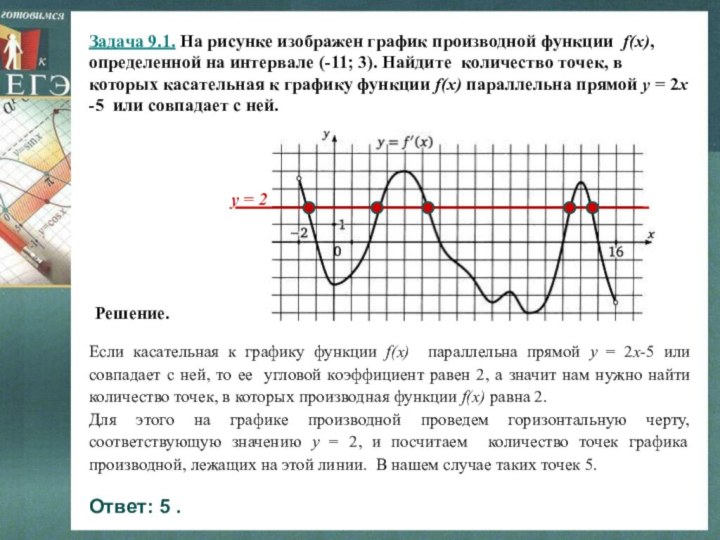
Если касательная к графику функции f(x) параллельна прямой y = 2x-5 или совпадает с ней, то ее угловой коэффициент равен 2, а значит нам нужно найти количество точек, в которых производная функции f(x) равна 2.
Для этого на графике производной проведем горизонтальную черту, соответствующую значению y = 2, и посчитаем количество точек графика производной, лежащих на этой линии. В нашем случае таких точек 5.
Решение.
y = 2
Ответ: 5 .
1
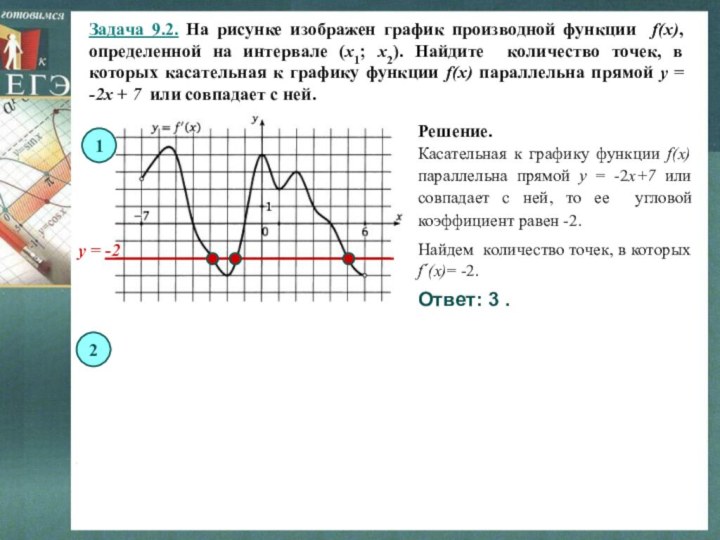
Решение.
Ответ: 3 .
Касательная к графику функции f(x) параллельна прямой y = -2x+7 или совпадает с ней, то ее угловой коэффициент равен -2.
Найдем количество точек, в которых f´(x)= -2.
Решение.
Поступим аналогично, найдем количество точек, в которых f´(x)= -2.
Ответ: 4 .
y = -2
y = -2
2
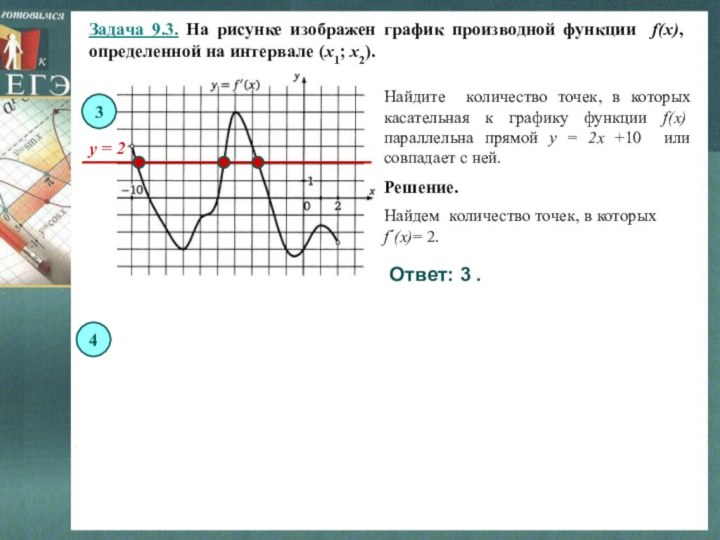
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2x +10 или совпадает с ней.
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -3x+8 или совпадает с ней.
Решение.
Ответ: 3 .
Найдем количество точек, в которых f´(x)= -3.
4
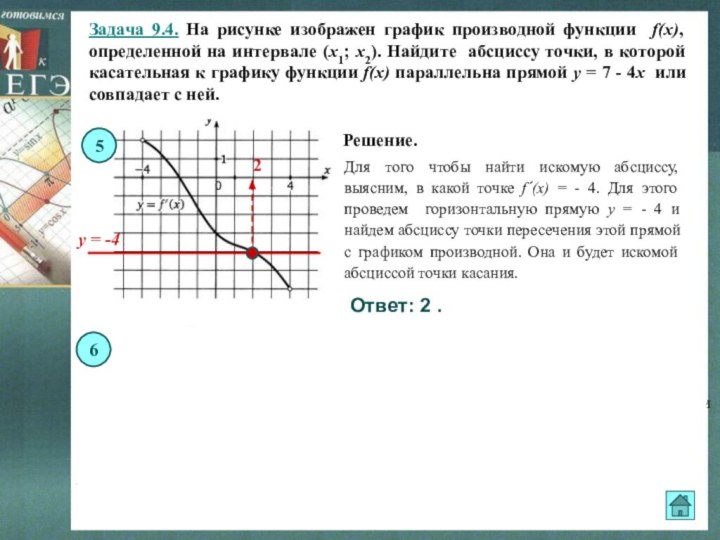
Для того чтобы найти искомую абсциссу, выясним, в какой точке f´(x) = - 4. Для этого проведем горизонтальную прямую y = - 4 и найдем абсциссу точки пересечения этой прямой с графиком производной. Она и будет искомой абсциссой точки касания.
Решение.
Ответ: 2 .
Решение.
Поступим аналогично, найдем точку, в которой f´(x) = - 4, проведем горизонтальную прямую y = - 4 и найдем абсциссу точки пересечения этой прямой с графиком производной.
Ответ: -1 .
5
6