- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логические законы
Содержание
- 2. Закон двойного отрицанияДвойное отрицание исключает отрицание
- 3. Переместительный (коммутативный) законДля логического сложения:Для логического умножения:
- 4. Сочетательный (ассоциативный) законДля логического сложения:Для логического
- 5. Распределительный (дистрибутивный) законДля логического сложения:Для логического умножения:
- 6. Закон общей инверсии ( законы де Моргана)Для логического сложения:Для логического умножения:
- 7. Закон идемпотентности (равносильности)Для логического сложения:Для логического умножения:Закон означает отсутствие показателей степени
- 8. Закон исключения константДля логического сложения:Для логического умножения:
- 9. Закон противоречияНевозможно, чтобы противоречащие высказывания были одновременно истинными.
- 10. Закон исключения третьегоИз двух противоречащих высказываний об
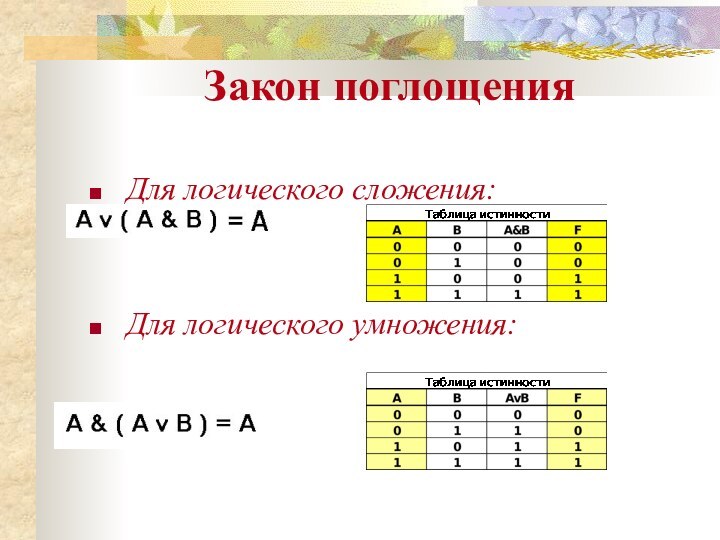
- 11. Закон поглощенияДля логического сложения:Для логического умножения:
- 12. Закон исключения (склеивания)Для логического сложения:Для логического умножения:
- 13. Пример По заданной логической функциипостроить логическую схему.
- 14. Построение необходимо начинать с логической операции, которая
- 15. ПримерНайдите X, еслиПо закону де Моргана
- 16. ПримерУпростите логическое выражение Правильность упрощения проверьте с помощью таблиц истинности для исходного и полученного логического выражения.
- 17. Согласно закону общей инверсии для логического сложения
- 18. Согласно закону противоречия:Согласно закону идемпотентности:Подставляя значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем:
- 19. Согласно закону исключения (склеивания) получаем:Подставляем значения и
- 20. Подставляем значения и получаем:Согласно распределительному (дистрибутивному) закону для логического умножения получается:Согласно закону исключения третьего:
- 21. Скачать презентацию
- 22. Похожие презентации
Закон двойного отрицанияДвойное отрицание исключает отрицание




















Слайд 4
Сочетательный
(ассоциативный) закон
Для логического сложения:
Для логического умножения:
При одинаковых
Слайд 6
Закон общей инверсии
( законы де Моргана)
Для логического
сложения:
Для логического умножения:
Слайд 7
Закон идемпотентности (равносильности)
Для логического сложения:
Для логического умножения:
Закон означает
отсутствие показателей степени
Слайд 9
Закон противоречия
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
Слайд 10
Закон исключения третьего
Из двух противоречащих высказываний об одном
и том же предмете одно всегда истинно, а второе
ложно, третьего не дано.Слайд 14 Построение необходимо начинать с логической операции, которая должна
выполняться последней. Т.к. в данном случае такой операцией является
логическое сложение, то на выходе логической схемы должен стоять дизъюнктор.





























