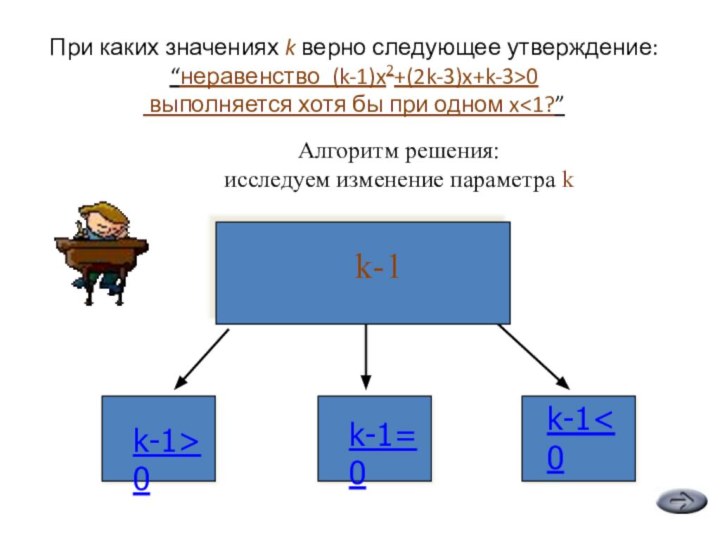
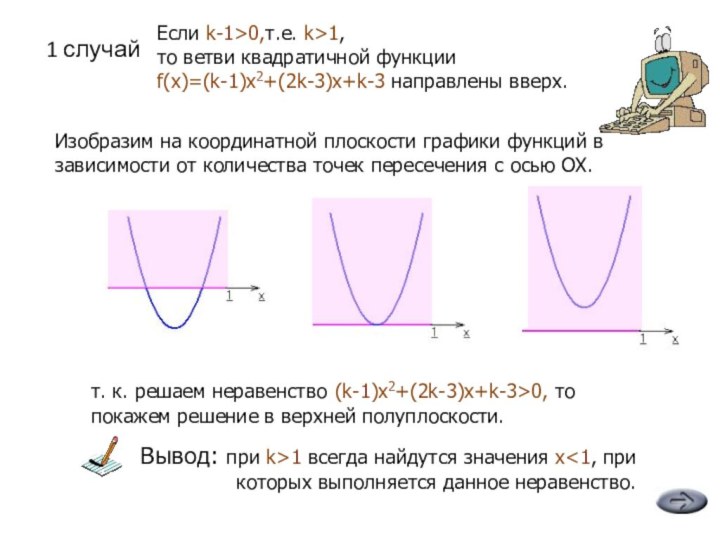
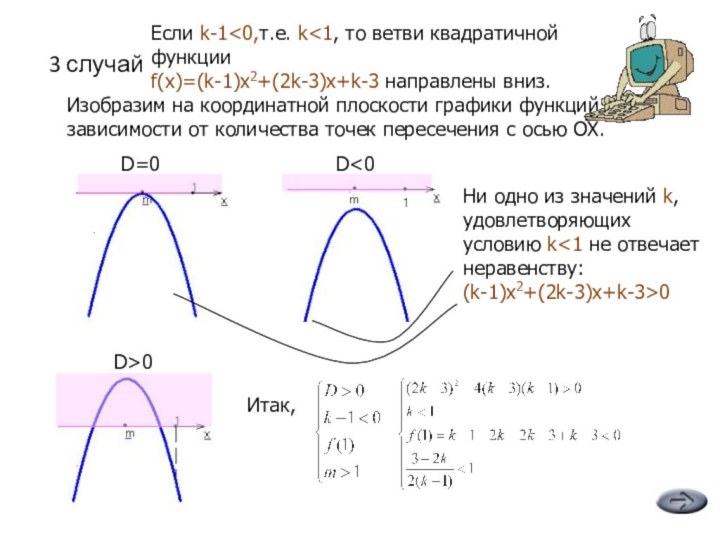
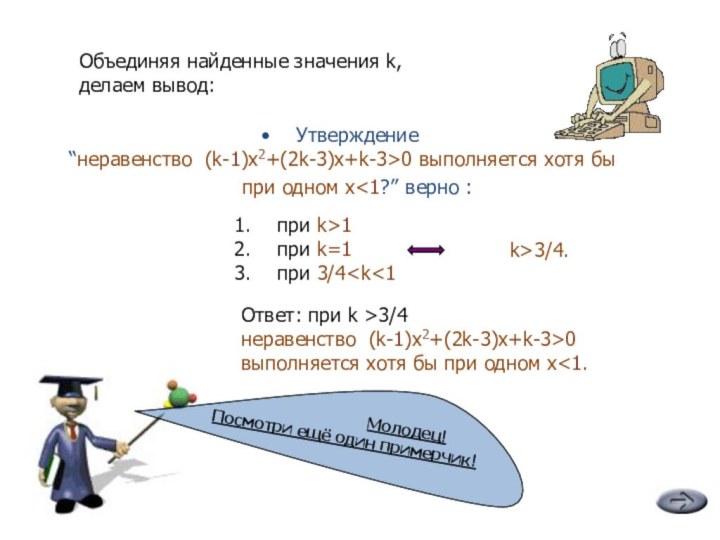
“неравенство (k-1)x2+(2k-3)x+k-3>0 выполняется хотя бы при одном x
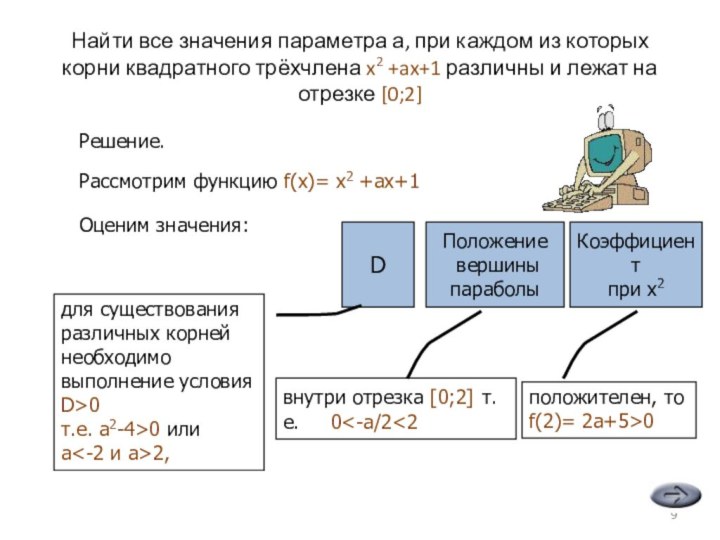
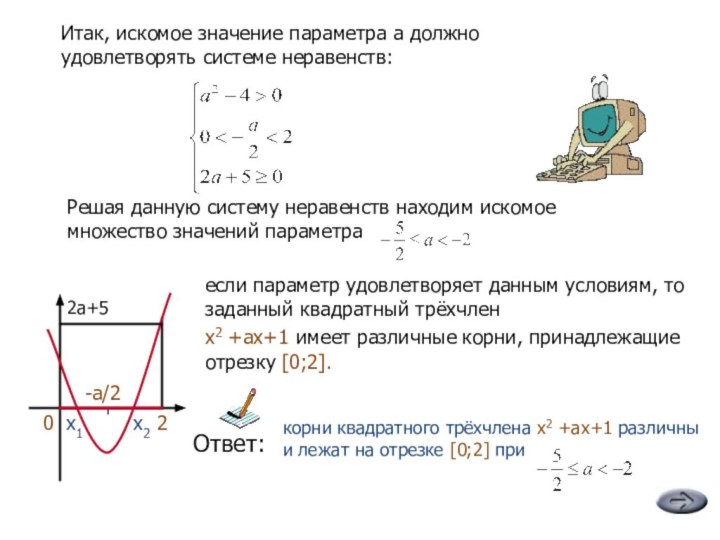
все значения параметра а, прикаждом из которых корни квадратного
трёхчлена x2 +ax+1 различны и лежат
на отрезке [0;2]?
Задание 3.
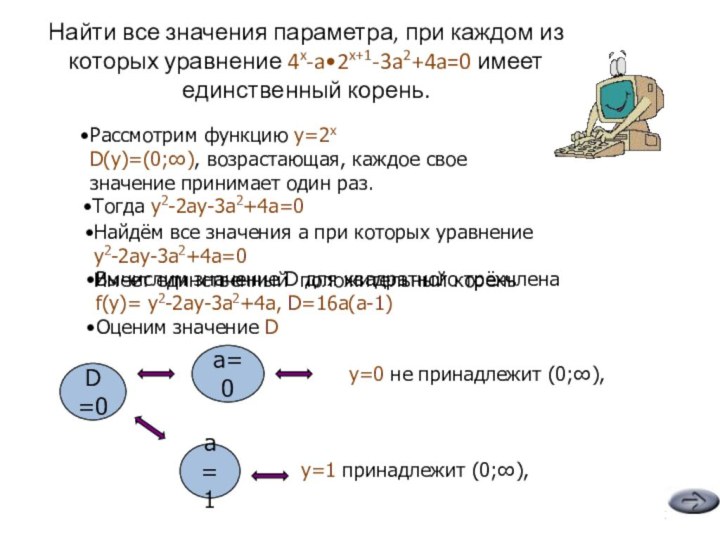
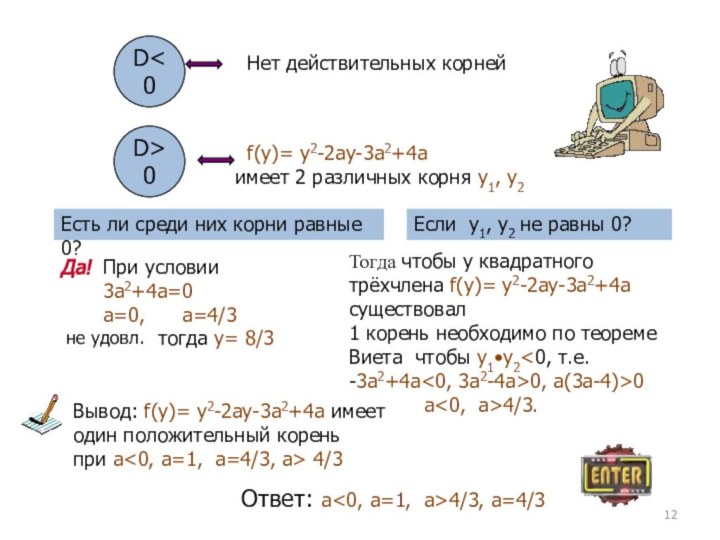
Найти все значения параметра, при каждом из которых уравнение 4x-a•2x+1-3a2+4a=0 имеет единственный корень.