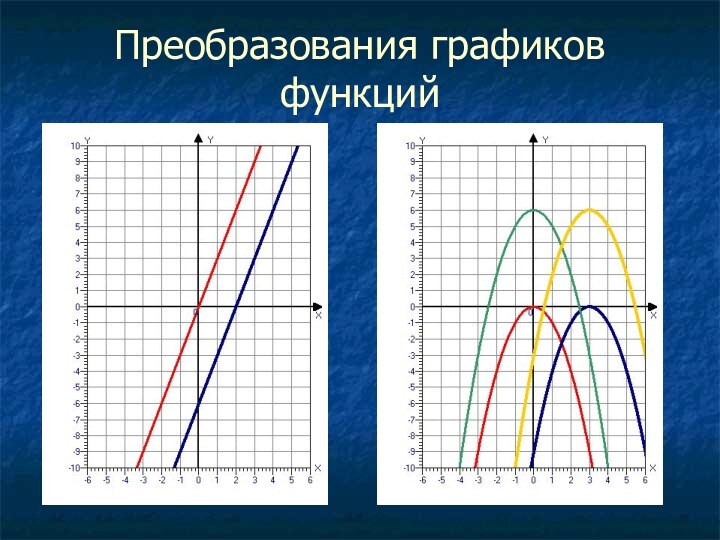
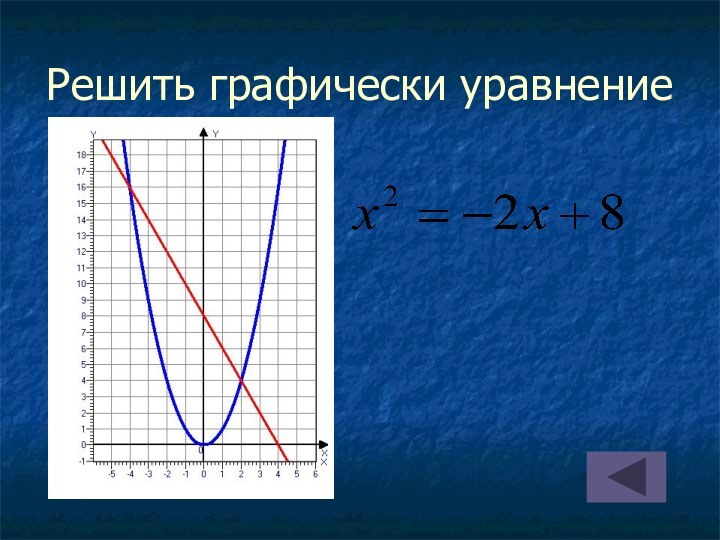
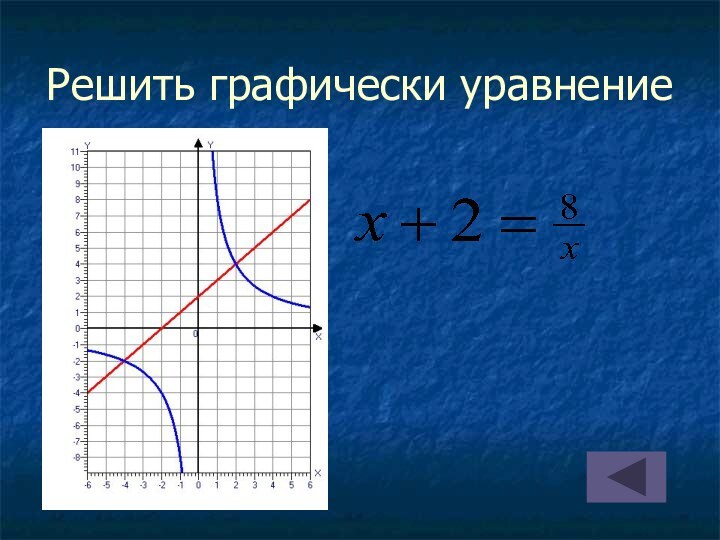
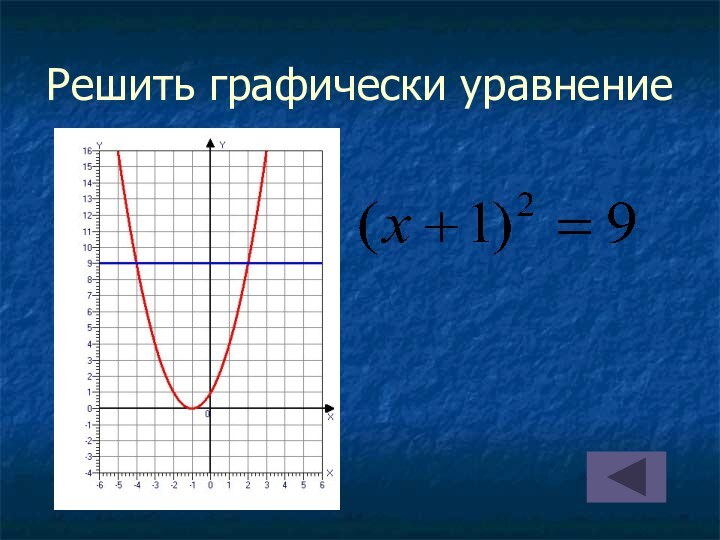
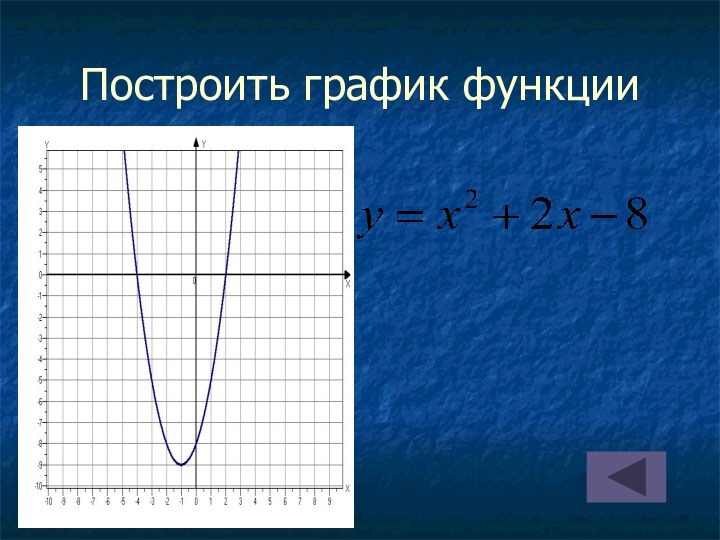
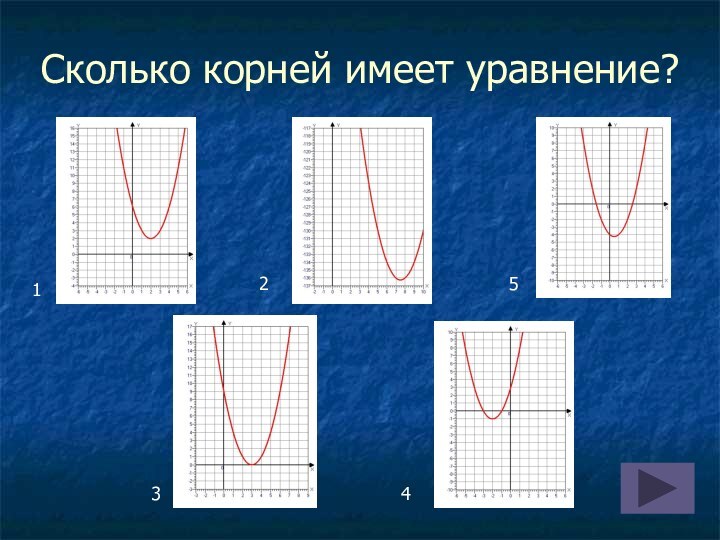
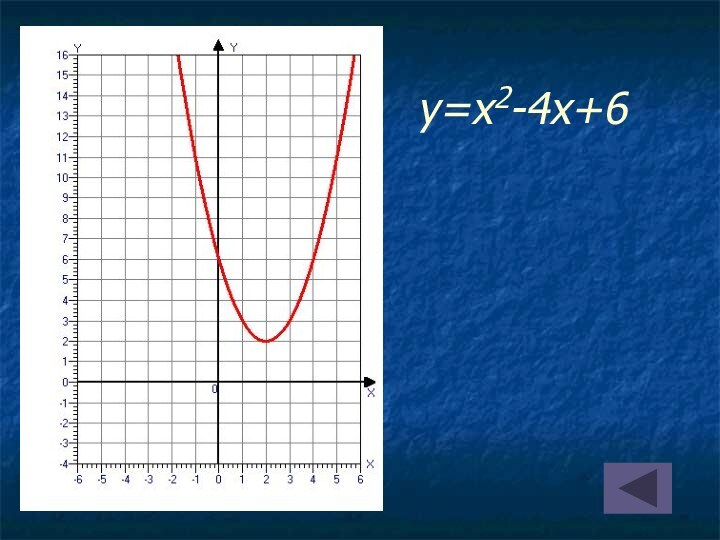
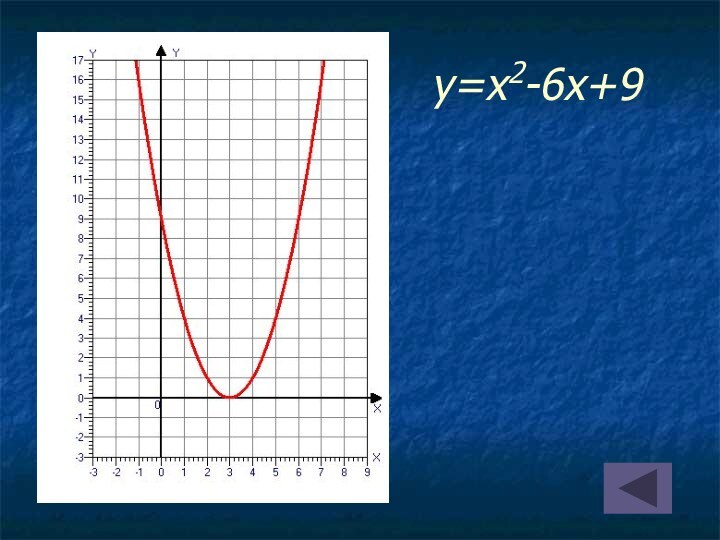
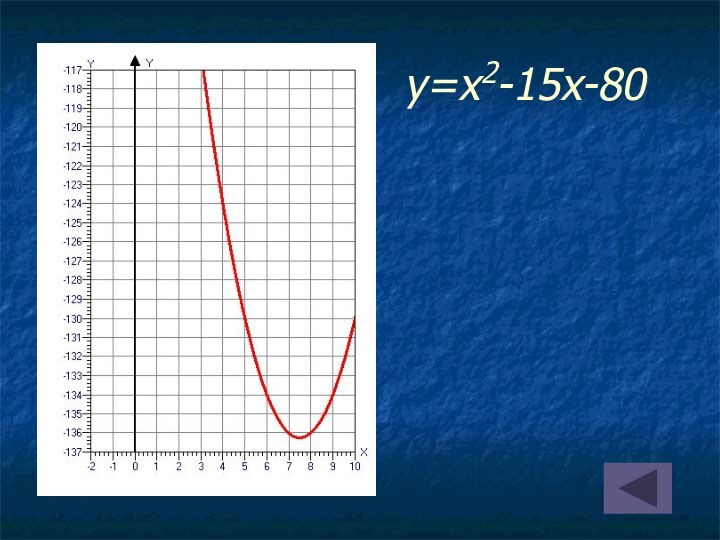
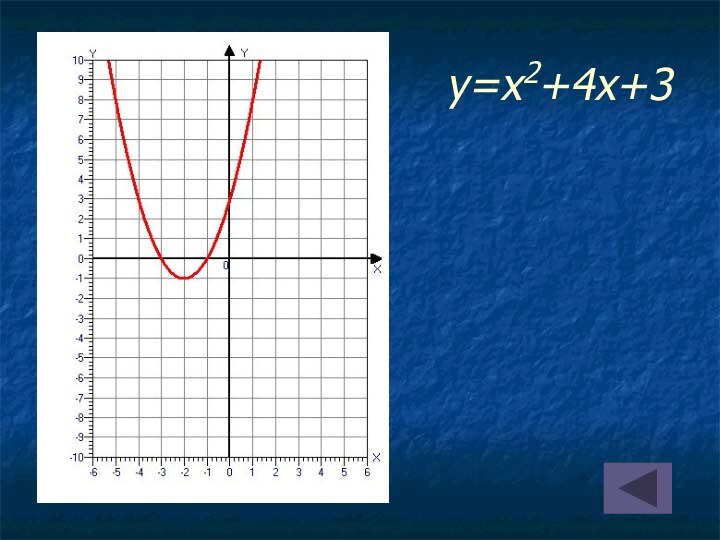
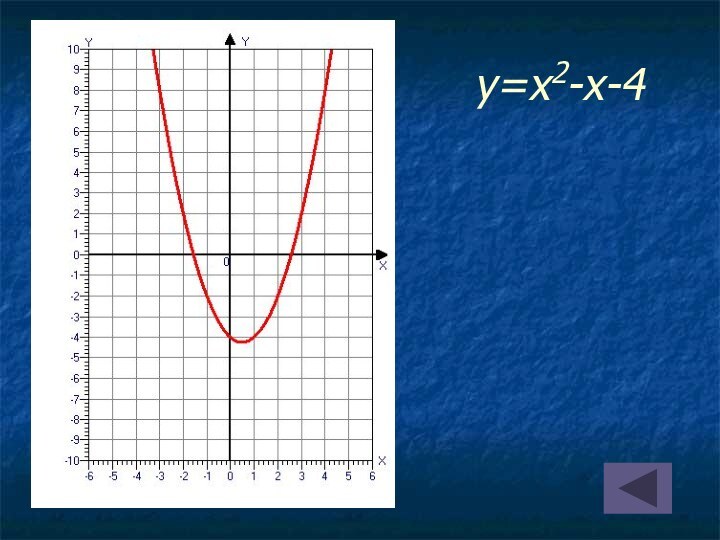
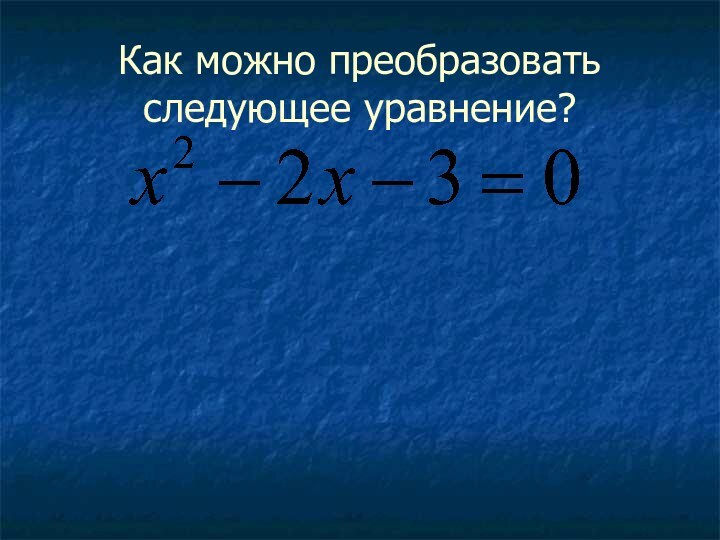на оси абсцисс две точки, симметричные относительно оси параболы;
найти значения функции в этих точках;провести параболу через полученные три точки.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графический способ решения квадратных уравнений
Содержание
- 2. Преобразования графиков функций
- 3. Преобразования графиков функций
- 4. Алгоритм построения параболынайти координаты вершины; провести ось
- 5. Решение уравнения Ответ: 1
- 6. Решить графически уравнение
- 7. Решить графически уравнение
- 8. Решить графически уравнение
- 9. Решить графически уравнение
- 10. Построить график функции
- 11. Как решить уравнение?Построить график квадратичной функции и
- 12. Как можно преобразовать следующее уравнение?
- 13. Способы преобразования:
- 14. Алгоритм решения квадратного уравнения графическим способомСпособ 1Построить график функции y=ax2+bx+cНайти точки пересечения графика с осью абсцисс
- 15. Алгоритм решения квадратного уравнения графическим способомСпособ 2Преобразовать
- 16. Алгоритм решения квадратного уравнения графическим способомСпособ 3Преобразовать
- 17. Алгоритм решения квадратного уравнения графическим способомСпособ 4
- 18. Алгоритм решения квадратного уравнения графическим способомСпособ 5Преобразовать
- 19. Сколько корней имеет уравнение?12345
- 20. y=x2-4x+6
- 21. y=x2-6x+9
- 22. y=x2-15x-80
- 23. y=x2+4x+3
- 24. y=x2-x-4
- 25. Скачать презентацию
- 26. Похожие презентации
Преобразования графиков функций
Слайд 4
Алгоритм построения параболы
найти координаты вершины; провести ось параболы;
отметить
провести параболу через полученные три точки.
Слайд 11
Как решить уравнение?
Построить график квадратичной функции и абсциссы
точек пересечения параболы с осью x будут являться корнями
уравнения.Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения.
Слайд 14
Алгоритм решения квадратного уравнения графическим способом
Способ 1
Построить график
функции y=ax2+bx+c
Найти точки пересечения графика с осью абсцисс
Слайд 15
Алгоритм решения квадратного уравнения графическим способом
Способ 2
Преобразовать уравнение
к виду
ax2 = -bx-c
Построить:
параболу y=ax2 и прямую y=-bx-c
Найти
точки их пересечения
Слайд 16
Алгоритм решения квадратного уравнения графическим способом
Способ 3
Преобразовать уравнение
к виду
ax2+с = -bx
Построить:
параболу y = ax2+с и
прямую y = -bxНайти их точки пересечения
Слайд 17
Алгоритм решения квадратного уравнения графическим способом
Способ 4
(выделение
полного квадрата)
Преобразовать уравнение к виду
a(x+l)2 = -m
Построить:
параболу y
= a(x+l)2 и прямую y = -mНайти точки их пересечения
Слайд 18
Алгоритм решения квадратного уравнения графическим способом
Способ 5
Преобразовать уравнение
к виду
Построить:
гиперболу
и прямую Найти точки их пересечения
