в другой – 15 тетрадей в линию.
Сколькими способами
можно выбрать 1 тетрадь в клетку или 1 тетрадь в линию?
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи по комбинаторике (9 класс)
Содержание
- 2. В одной пачке лежит 10 тетрадей в
- 4. Поэтому, если объект а можно выбрать n
- 5. Задача 2. В первой пачке
- 7. Поэтому, если объект а можно выбрать n
- 8. Это правило в комбинаторике называется «правило произведения».
- 9. Задача 1. Сколько двузначных чисел можно составить
- 11. Задача 3.(с помощью геометрической интерпретации – «деревом
- 13. З1З3З4(С 2;З(С 3;З(С 4;З(С5;З(С6;З
- 14. Работа в парахВ столовой предлагают 2 различных
- 15. Дерево возможных вариантов: А1А2 В1В2В3В1В2В3С1С1С1С1С1С1С2С2С2С2С2С2О
- 16. Решение:(А1,В1,С1);(А1,В1,С2);(А1,В2,С2);(А1,В2,С3);(А1,В3,С1);(А1,В3,С2);(А2,В1,С1);(А2,В1,С2);(А2,В2,С1);(А2,В2,С2);(А2,В3,С1);(А2,В3,С2).Ответ: 12=2×3×2
- 17. Домашнее задание: творческая
- 18. Скачать презентацию
- 19. Похожие презентации
В одной пачке лежит 10 тетрадей в клеточку, в другой – 15 тетрадей в линию. Сколькими способами можно выбрать 1 тетрадь в клетку или 1 тетрадь в линию?
Слайд 2
В одной пачке лежит 10 тетрадей в клеточку,
в другой – 15 тетрадей в линию.
можно выбрать1 тетрадь в клетку или 1 тетрадь в линию?
Слайд 3
Решение.
Из первой пачки тетрадь в
клетку можно взять 10 способами,
а из второй – 15 способами.
Значит, всего существует
10+15=25 способов.
Слайд 4
Поэтому, если объект а можно
выбрать n способами,
а объект в – т способами,
то выбор «или
а или в» можноосуществить ( n+т) способами.
Это правило в комбинаторике
называется «правило суммы».
Слайд 5
Задача 2.
В первой пачке
10
тетрадей зеленого цвета,
во второй 15 тетрадей желтого цвета.
Сколькими способами можно
взять 1 зеленую и 1 желтую тетрадь?
Слайд 6
Решение:
Зеленые тетради можно выбрать
10 способами,
а желтые – 15 способами.
Значит, 1 зеленую и 1 желтую тетрадь
можно выбрать 10×15=150 способами.
Слайд 7
Поэтому, если объект а можно
выбрать n способами,
а объект в – т способами,
то выбор «
а и в» можно осуществить( nm) способами
Слайд 9
Задача 1.
Сколько двузначных чисел можно
составить из
цифр 2;3;4.
Решение.
Имеем: 22 23 2432 33 34
42 43 44
Числа разбились на 3 группы по 3 числа
в каждой – отсюда и правило умножения
при подсчете таких комбинаций.
Ответ: 3×3=9
Слайд 10
Задача 2:
Из города А в город В ведут две дороги,
из города В в город С – 3 дороги,
из города С до пристани - две дороги (см. рис.1).
Туристы хотят проехать из города А
через город В и С к пристани. Сколькими способами,
они могут выбрать маршрут? Решение:
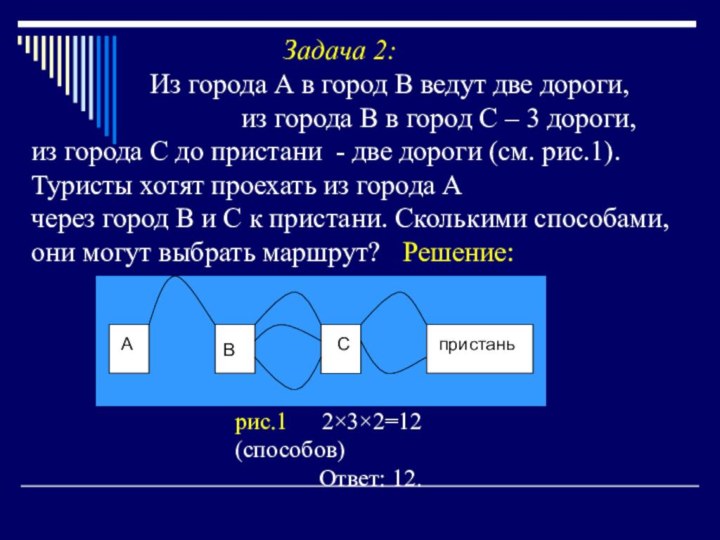
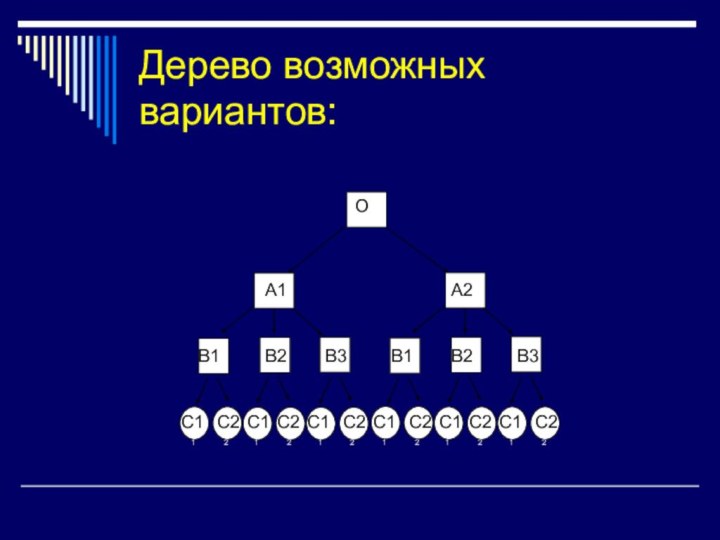
рис.1 2×3×2=12 (способов)
Ответ: 12.
А
В
С
пристань
Слайд 11
Задача 3.
(с помощью геометрической
интерпретации –
«деревом возможных
вариантов»)
Пусть существует 3 кандидата: С1, С2, С3
на место
старосты класса и 2 кандидата на место его заместителя:
З1 и З2.
Сколькими способами можно
избрать актив класса,
состоящий из старосты и его заместителя?
Слайд 12
Решение.
Старосту можно выбрать 3 способами,
2 способами его заместителя.
Поэтому общее число способов
равно 3×2=6
Правило умножения
для трех и более испытаний
можно объяснить
с помощью геометрической модели,
которую называют
«деревом возможных вариантов».
Слайд 14
Работа в парах
В столовой предлагают 2 различных первых
блюда А1 и А2, 3 различных вторых блюда В1,
В2 и В3 и два вида десерта С1 и С2. Сколько различных обедов из 3х блюд может предложить столовая?Найти решение с помощью «дерева возможных вариантов»
Слайд 16
Решение:
(А1,В1,С1);(А1,В1,С2);(А1,В2,С2);(А1,В2,С3);
(А1,В3,С1);(А1,В3,С2);(А2,В1,С1);(А2,В1,С2);
(А2,В2,С1);(А2,В2,С2);(А2,В3,С1);(А2,В3,С2).
Ответ: 12=2×3×2
Слайд 17 Домашнее задание: творческая работа (реферат, презентация,
проект, «дерево возможных вариантов») по теме «Комбинаторика» (по желанию).
Итог
урока:что изучает комбинаторика?
назовите основные правила комбинаторики,
что такое «дерево возможных вариантов»?
творческая работа (реферат, проект, «
