- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тема урока: Разложение многочлена на множители. Вынесение общего множителя за скобки и методом группировки.
Содержание
- 2. Оценочный лист
- 3. Проверка домашнего задания
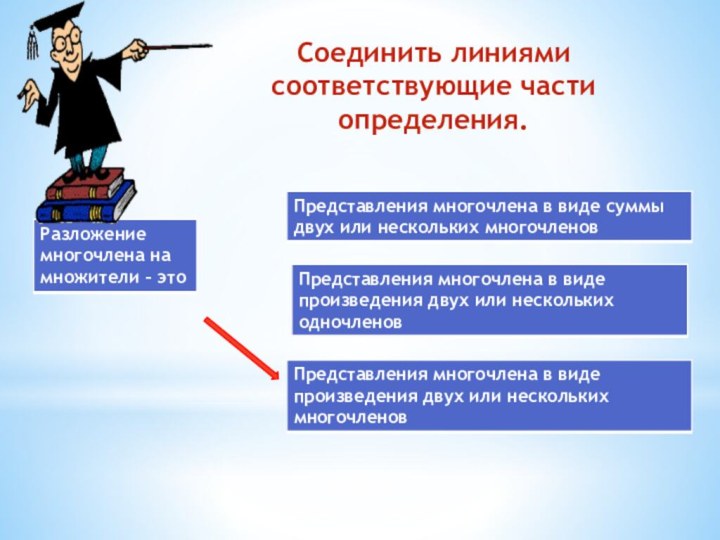
- 4. Соединить линиями соответствующие части определения.
- 5. Восстановить порядок выполнения действия при разложении многочлена на множители способом группировки. 123
- 6. Завершить утверждение. Представление многочлена в виде произведения
- 7. Задание №1Разложите на множители:3x – 6;10a2 – a;15x2 + 3x;22x2 – 11x;-16х2+9х.
- 8. Задание №1. Ответы.Разложите на множители:3x – 6=
- 9. Задание №2. Вставьте
- 10. Вариант 1.1. ( х - у )2
- 11. Постановка темы и цели урока. Мотивация
- 12. Тема урока: «Разложение многочлена на множители. Вынесение
- 13. 4c·(4c – 1) – 3· (4c –
- 14. Иногда удаётся такая группировка, что в каждой
- 15. =m·(2x-3) - 2· (2x-3) = (2x-3) ·(m-2)Члены
- 16. x2 – 8x +15 == x2 –
- 17. Решение уравнений методом разложения на множители заключается
- 18. Задание. «Математическая эстафета». Задания
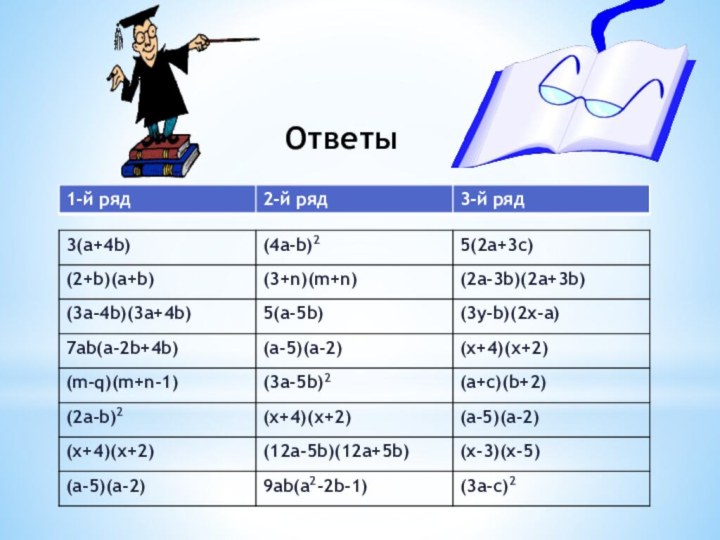
- 19. Ответы
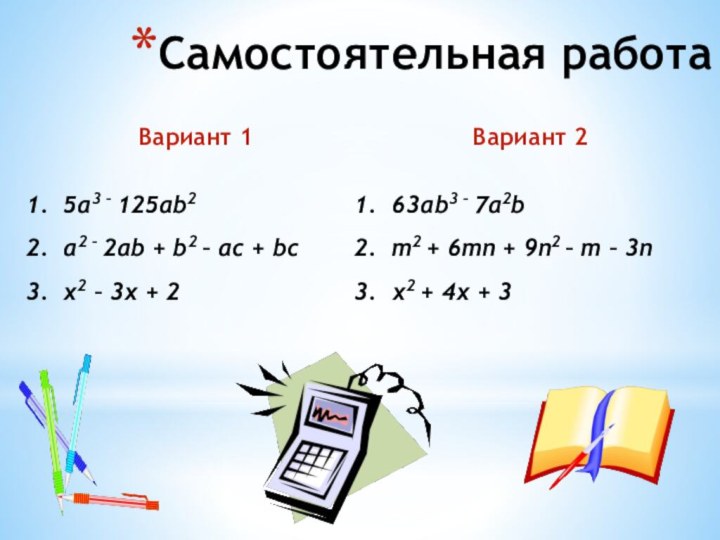
- 20. Самостоятельная работа
- 21. Ответы
- 22. Итоги урока. Рефлексия учебной деятельности на
- 23. Скачать презентацию
- 24. Похожие презентации



















Слайд 5 Восстановить порядок выполнения действия при разложении многочлена на
множители способом группировки.
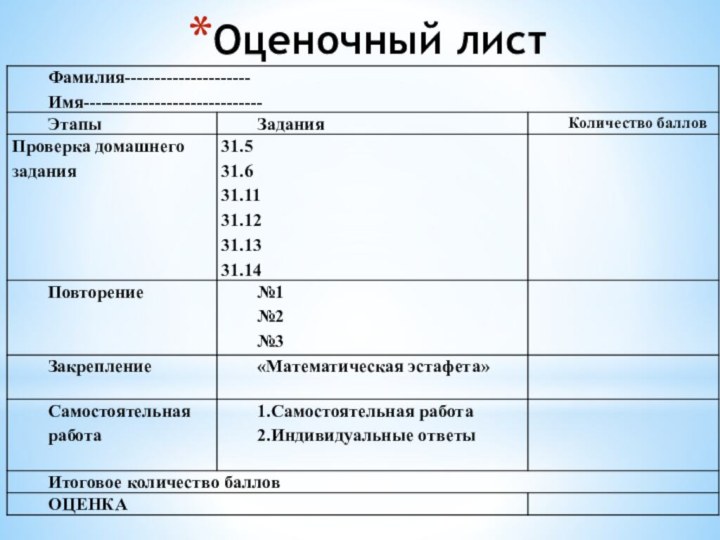
Слайд 6
Завершить утверждение.
Представление многочлена в виде произведения одночлена
и многочлена называется
вынесением общего множителя за скобки.
Слайд 8
Задание №1. Ответы.
Разложите на множители:
3x – 6= 3(х-2)
10a2
– a= а(10а-1)
15x2 + 3x= 3х(5х-1)
22x2 – 11x= 11х(2х-1)
-16х2+9х
= х(-16х + 9)Слайд 9 Задание №2. Вставьте одночлен
так,
чтобы полученное равенство было верным:
а) 18ab + 16b
= . . .(9a + 8);б) 4ас2 + 6а3с3- 2а2с = 2ас (. . .+ . . . - …);
в) ab – ac + b2 – bc = (ab - . . .)+(. . . – bc) =
=. . (b – c) + b(. . – c) = . . .
г) 4с2 - . . . = (. . . – 5)(. . . + . .)
Найдите неизвестное слагаемое,
чтобы получилась формула сокращённого умножения:
д) a2 + 8a + . . .;
e) 100b2 - . . . . +4c2.
2b
2c
3a2c2
a
аc
b2
a
b
(b – c)(a + b)
16
40bc
25
2с
5
2с
Слайд 10
Вариант 1.
1. ( х - у )2 =х2
- 2ху + у2;
2. ( а – b )(
а + b ) = a2 - 2аb + b2; 3. а3 - b3 = ( а + b)( а2 – аb + b2);
4.( а + b )2 = а2 + аb + в2;
5. а3 + b3 = ( а + b)( а2 – аb + b2);
Вариант 2.
1. ( а - b)( а + b) = а2 - b2 ;
2. ( х – у )2 = х2 + ху + у2;
3. а3 + b3 = ( а - b)( а2 – аb + b2);
4. а3 - b3 = ( а + b)( а2 + аb + b2);
5. ( а + b )2 = а2 + 2аb + b2;
КЛЮЧ ОТВЕТОВ: 10001
1- истина, 0 – ложь.
Задание №3
Слайд 11 Постановка темы и цели урока. Мотивация учебной
деятельности учащихся.
Какими методами раскладывали многочлен на множители? Исходя из
предыдущих этапов урока сформулируйте тему урока и запишите ее в тетрадь.Продолжите фразу: «закрепить навыки……..», тем самым формулируя цель урока.
Что вас мотивирует на успешную деятельность?
Слайд 12 Тема урока: «Разложение многочлена на множители. Вынесение общего
множителя за скобки и методом группировки».
Цели урока:
Закрепить навык вынесения
общего множителя за скобки и метода группировки при разложения многочлена на множители;Формировать умение самостоятельно определять цели своего обучения;
Формировать умение осуществлять контроль своей деятельности в процессе достижения результата.
Слайд 13 4c·(4c – 1) – 3· (4c – 1)2
=
*) Иногда алгебраическое выражение задается в таком виде, что
в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов:= 4c·(4c – 1) – 3· (4c – 1) ·(4c – 1) =
= (4c – 1) · (4c – 3 ·(4c – 1)) =
= (4c – 1) · (4c – 12c + 3) =
= (4c – 1) · ( – 8c + 3) = (4c – 1) · ( 3 – 8c)
Слайд 14 Иногда удаётся такая группировка, что в каждой группе
после вынесения общих множителей, в скобках остается один и
тот же многочлен, который, в свою очередь, может быть вынесен за скобки как общий множитель.Тогда говорят, что разложение многочлена на множители осуществлено способом группировки.
Способ группировки применяется, когда члены многочлена не имеют общего множителя.
Слайд 15
=m·(2x-3) - 2· (2x-3) = (2x-3) ·(m-2)
Члены многочлена
не имеют общего множителя:
Составим две группы: в первую включим
1 и 2 член,во вторую – 3 и 4:
2mx - 3m - 4x + 6 = ?
2mx - 3m - 4x + 6 = (2mx - 3m) +(- 4x + 6) =
= (2x·m - 3·m) +(- 2x·2 + 3·2) =
Слайд 16
x2 – 8x +15 =
= x2 – 3x
– 5x +15 =
*) Разложите на множители,
представив один
из членов многочлена в виде суммы подобных слагаемых:
= (x2 – 3x) + (– 5x +15) =
= x·(x – 3) – 5·(x – 3) =
= (x – 3) ·(x– 5).
Слайд 17 Решение уравнений методом разложения на множители заключается в
следующем: если p(х)= p1(х)· p2(х)·… ·p n(х), то всякое
решение уравнения p(х)=0 является решением совокупности уравнений p1(х)=0; p2(х)=0; … ; p n(х)=0.2·х2 + х – 6 = 0
(2·х – 3)·(х+2)=0
2х2 + 4х – 3х – 6=0
(2·х2 + 4х ) +(-3х – 6) = 0
2х(х + 2 ) -3(х +2) = 0
либо 2·х – 3=0,
либо х+2=0.
Значит,
2·х = 3
х =1,5
х = – 2
Ответ: 1,5 и -2
Слайд 22
Итоги урока. Рефлексия учебной деятельности на уроке.
На
каких этапах урока у вас возникли затруднения? В каких
номерах?Продолжите фразу:
а) я добился цели ….;
б) я научился …..;
в) я узнал….;
г) я работал на оценку…. .