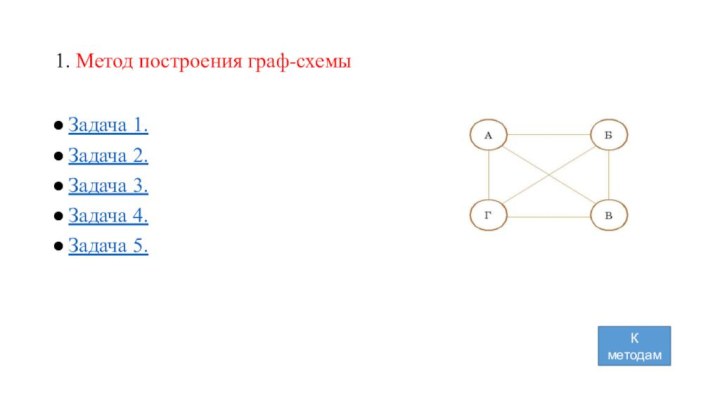
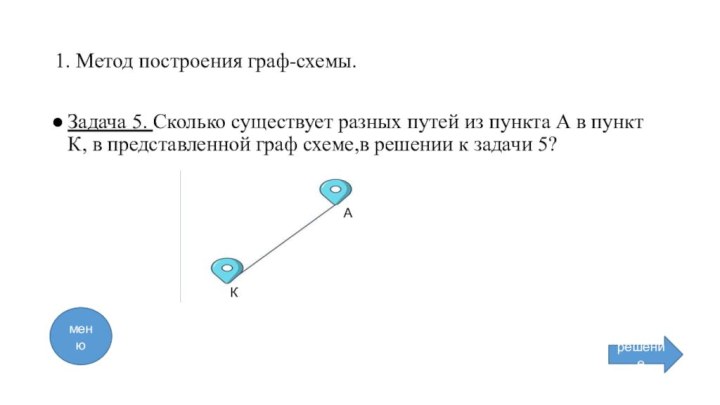
Метод построения дерева возможных вариантов решений
3. Метод перебора возможных
вариантов4. Табличный метод
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





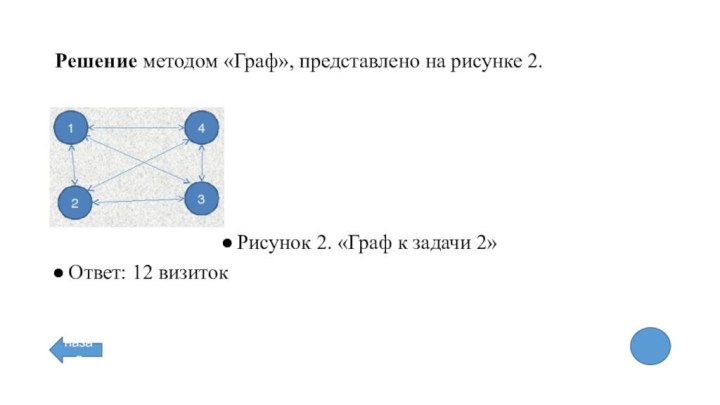



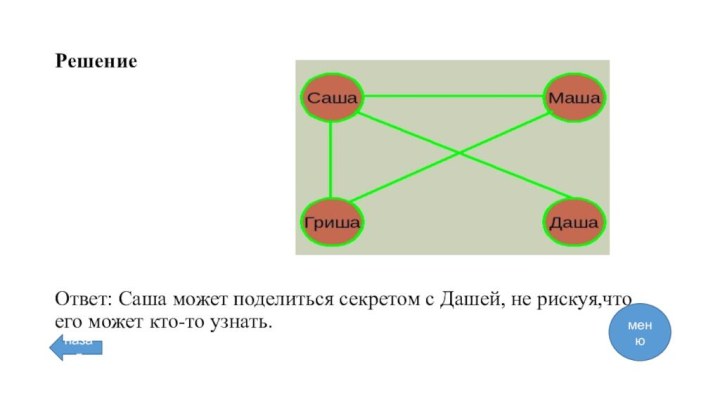





























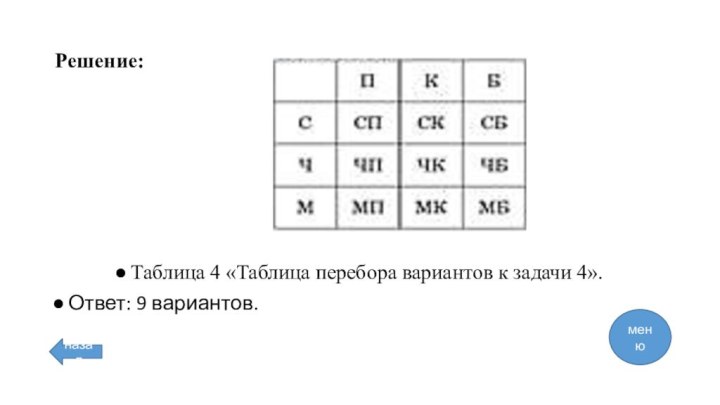
решение
меню
решение
меню
меню
решение
решение
меню
решение
меню
А
К
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
назад
меню
решение
меню
решение
меню