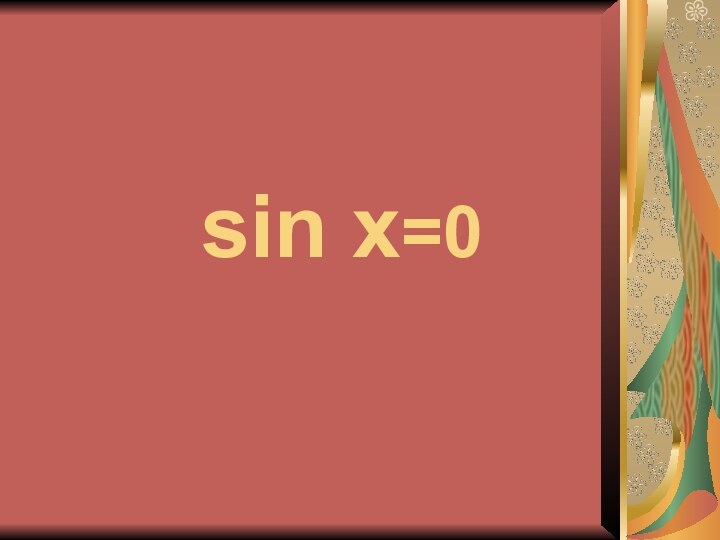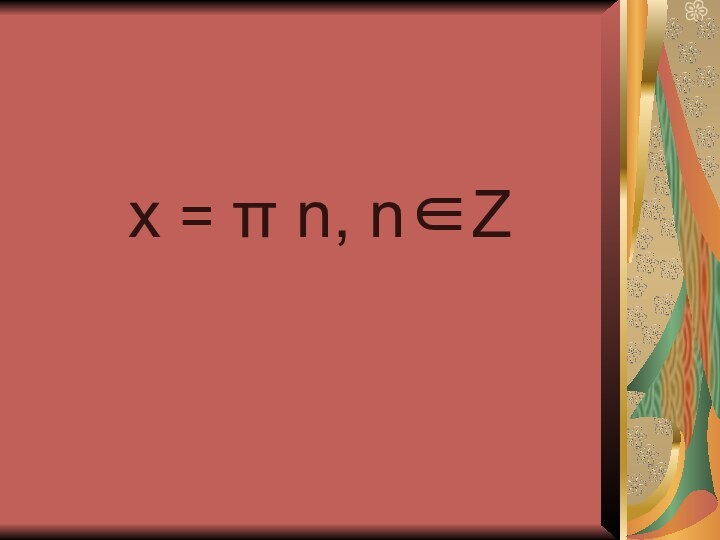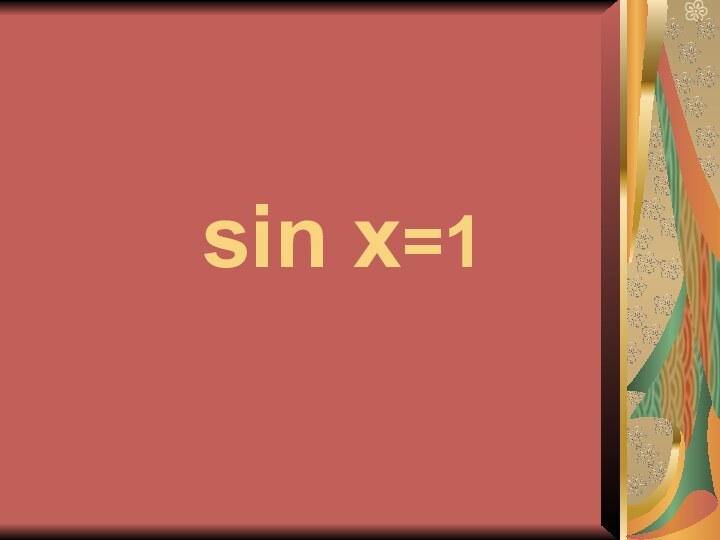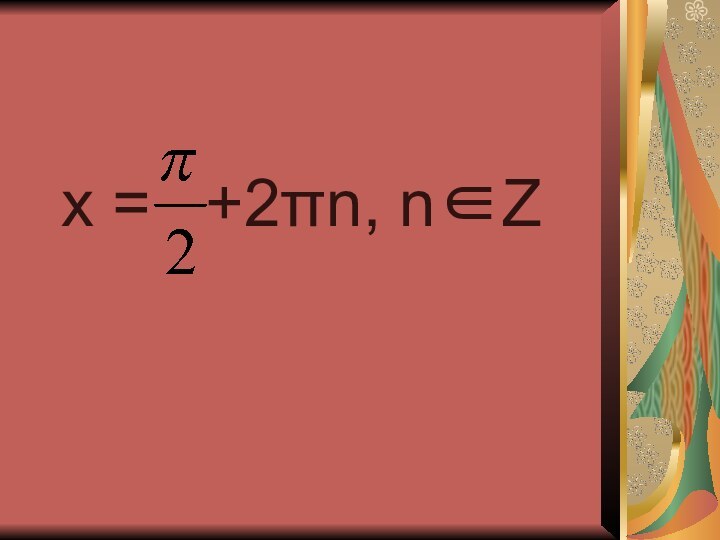Слайд 2
Цели урока:
Создания условий для осознанного усвоения решения тригонометрических
уравнений вида
a sinx + b cosx = c.
Формирование
навыков самоконтроля и взаимоконтроля, алгоритмической культуры учащихся.
Развитие устной математической речи. Обеспечение условий для развития умения решать тригонометрические уравнения, совершенствовать мыслительные умения старшеклассников: сравнивать, обобщать и анализировать, развития навыков обработки информации.
Развитие коммуникативных умений делового общения сверстников. Воспитание аккуратности.
Слайд 3
Проверка домашнего задания
sin7x – sin x =cos4x
Слайд 4
Решение.
sin7x – sin x =cos4x,
2sin3x cos4x - cos4x
=0,
сos4x ( 2sin3x – 1 )=0,
сos4x=0 или 2cos3x -1
=0
сos4x=0
4x =П/2+Пn, n € Z; cos3x =1/2,
X=П/8 +Пn/4, n € Z, 3x =±аrccos1/2 +2Пn, n
3x =±П/3 +2Пn, n € Z,
X =±П/9 + 2/3Пn, n € Z.
Ответ: X=П/8 +Пn/4, X =±П/9 = 2/3Пn, n € Z
Слайд 5
Решить уравнение
sin²x - cos²x = cos4x
Слайд 6
Решение.
sin²x-cos²x =cos4x ,
- (cos² - sin²x )=cos4x
,
-cos2x = cos²2x - sin²2x,
-cos2x = cos²2x – (
1 - cos²2x),
-cos2x - cos²2x +1 - cos²2x = 0,
-2cos²2x – cos2x +1 = 0,
2cos²2x + cos2x -1 = 0.
Заменим сos2x на У , где |У|≤1
Тогда 2 у² +у -1 = 0,
D =1 - 4•2•(-1) =9,
У =1/ 2, у = -1.
Выполним обратную замену
Cos2x =1/ 2 , cos2x = -1,
2x = П+2Пn, n € Z,
2x =±arccos1/2 =2Пn , n € Z, x=П/2+Пn, n € Z.
2x ±П/3 +2Пn. n € Z,
X =±П/6+Пn, n € Z.
Ответ: X =±П/6+Пn, x=П/2+Пn, n € Z.
Слайд 7
Решение уравнений учащимися
№628 (1)
№628 (3)
№629 (2)
Слайд 9
x = ± arccos a + 2πn,
n∈Z
arccos
(– a) = π - arccos a
Слайд 11
x=(–1)narcsin a + πn,
n ∈Z
arcsin (–
a) = – arcsin a
Слайд 13
x = arctg a + πn,
n ∈Z
arctg
(– a) = – arctg a
Слайд 26
Решить уравнение
4sin²x – 4sinx – 3 = 0
2cos²x
– sinx – 1 = 0
Слайд 27
Ответы.
4sin²x - 4 sinx – 3 = 0
( -1)n+1 П/6 +Пn, n Z.
2 сos²x – sin x – 1 = 0
±П/6 +Пn; -П/2+2Пn, n Z.
.
Уравнение
.
Поделив уравнение на , получим , ,
При решении этой задачи обе части уравнения были поделены на .
Напомним, что при делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения корнями данного уравнения. Если , то из уравнения следует, что . Однако и
не могут одновременно равняться нулю, так как они связаны
равенством . Следовательно, при делении
уравнения , где , , на (или ) получаем уравнение, равносильное данному.
.
Используя формулы sin x = 2 sin cos , cos x = cos2 - sin2 и
записывая правую часть уравнения в виде ,
получаем
Поделив это уравнение на ,
получим равносильное уравнение
Обозначая , получаем , откуда .
1)
2)
Ответ:
Слайд 32
Данное уравнение является уравнением
вида
, (1)
где , , , которое можно решить другим способом.
Разделим обе части этого уравнения на :
. (2)
Введем вспомогательный аргумент , такой, что
.
Такое число существует, так как
.
Таким образом, уравнение можно записать в виде
.
Последнее уравнение является простейшим тригонометрическим уравнением.