- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Признаки возрастания и убывания функции
Содержание
- 2.
- 4. Определение Правило, или закономерность,
- 5. ОпределениеЕсли в области определения функции y=f(x) для
- 7. Теорема Если для функции f(x) в
- 8. Если для любого х из промежутка Х
- 9. Следовательно, с помощью производной для любой функции
- 10. Примечание: 1.Если функция f(x) непрерывна на концах
- 11. Пр.1 (№261(в))Найти промежутки возрастания и убывания функции
- 14. /
- 22. Скачать презентацию
- 23. Похожие презентации
Определение Правило, или закономерность, при котором каждому значению х, из множества Х соответствует единственное значение у из множества У, называется функцией. Определение Множество значений независимой переменной, при котором функция принимает




















Слайд 5
Определение
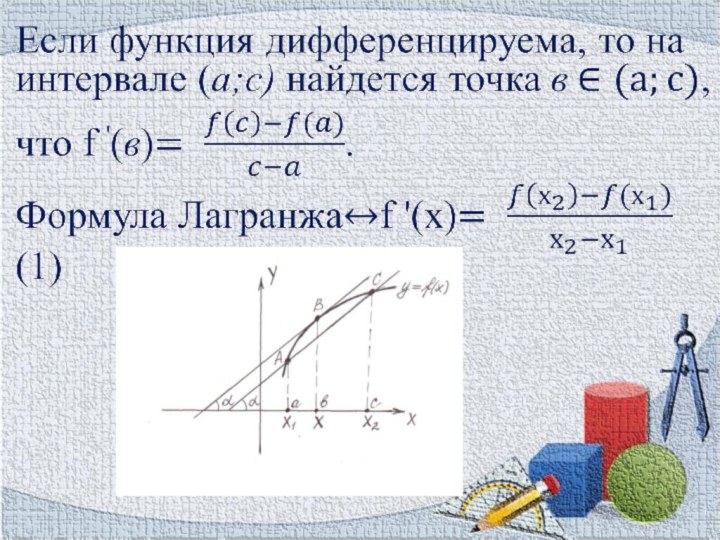
Если в области определения функции y=f(x) для любых
чисел х1< х2 выполняется неравенство f(x1)< f(x2) (f(x1)> f(x2)),
то функция называется возрастающей (убывающей) функцией
Слайд 7
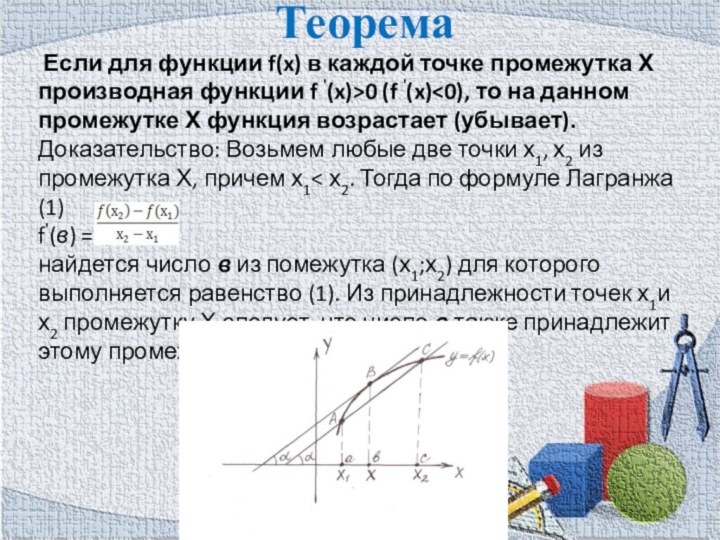
Теорема
Если для функции f(x) в каждой точке
промежутка Х производная функции f '(x)>0 (f '(x)
на данном промежутке Х функция возрастает (убывает). Доказательство: Возьмем любые две точки х1, х2 из промежутка Х, причем х1< х2. Тогда по формуле Лагранжа (1) f'(в) = найдется число в из помежутка (х1;х2) для которого выполняется равенство (1). Из принадлежности точек х1и х2 промежутку Х следует, что число в также принадлежит этому промежутку.Слайд 8 Если для любого х из промежутка Х выполняется
условие f '(x)>0,тогда f '(в)>0, а по предположению х2-х1>0,
из равенства (1) следует, чтоf(х2) - f(х1)>0 или f(х1)< f(х2).
Следовательно, по определению возрастающей функции f(х) - возрастающая функция.
Если же для любого х из промежутка Х выполняется условие f '(x)<0, тогда f '(в)<0, а по предположению х2-х1>0, из равенства (1) следует, что f(х2) - f(х1)<0 или f(х1)> f(х2).
Следовательно, по определению убывающей функции
f(х) – убывающая функция.
Слайд 9 Следовательно, с помощью производной для любой функции можно
найти промежутки возрастания и убывания и при этом используется
следующий алгоритм:найти область определения функции;
2) вычислить производную функции;
3) решить неравенство f '(x)>0 или f '(x)<0;
4) используя утверждение теоремы найти промежутки возрастания и убывания функции.
Слайд 10
Примечание:
1.Если функция f(x) непрерывна на концах промежутка,
то эти точки входят в данный промежуток.
2. Для решения
неравенств f '(x)>0 и f '(x)<0 удобно пользоваться обобщением метода интервалов (теоремой Дарбу): точки, в которых производная равна нулю или не существует, разбивают область определения функции f(х) на промежутки, в каждом из которых f '(x) сохраняет постоянный знак. Знак можно определить, вычислив значение f '(x) в какой-нибудь точке.
Слайд 11
Пр.1 (№261(в))
Найти промежутки возрастания и убывания функции
у=х2 – 6х
решение:
1. D(f(x))=(-∞;+∞)
2. f '(x)=(х2-6х)'=2х-6
3. 2х-6>0, 2х-6
метод интервалов:2х-6=0, х=3(рисунок)4. при х<3, получаем f '(x)<0. Тогда по теореме на промежутке (-∞;3] функция убывает, а при х>3, получаем f '(x)>0, поэтому на промежутке [3;+ ∞) функция возрастает.