Презентация на тему по алгебре и началам анализа на теме Максимумы и минимумы. (11 класс)

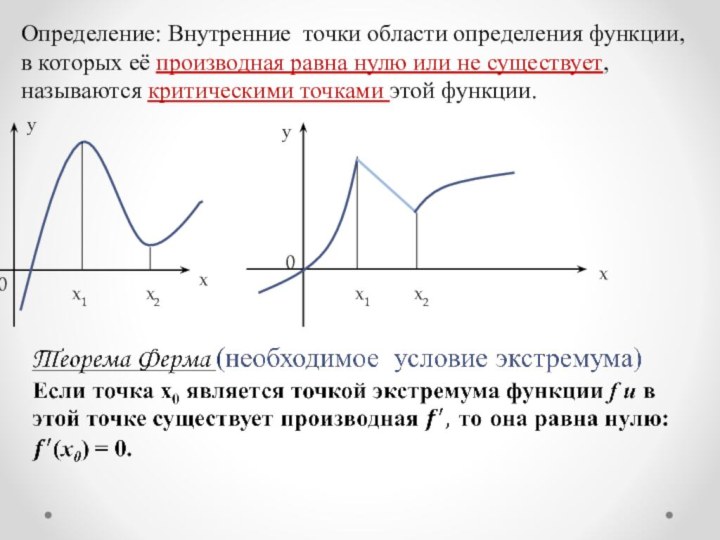
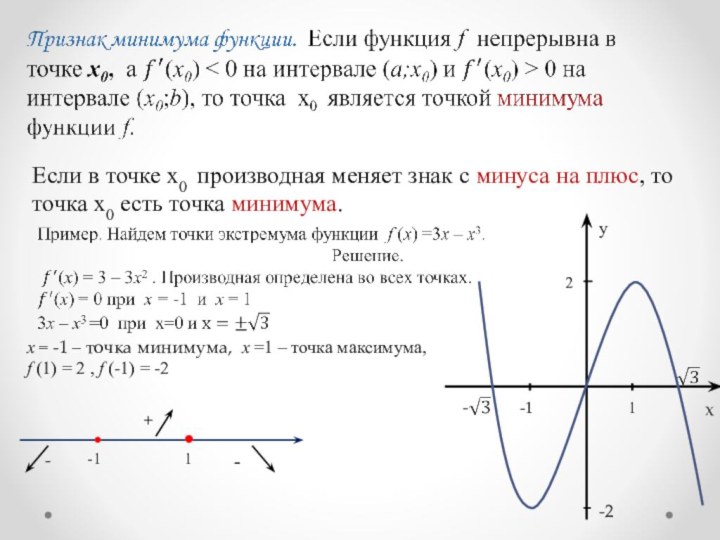
Рассмотреть теорему Ферма, которая является необходимым условием экстремума функции;
3)

Вывести признак максимума функции и признак минимума функции;
4) Научиться решать задачи на данную тему, используя полученные знания
РАЗВИВАЮЩАЯ :
1) Способствовать развитию общения как метода научного познания,
аналитико-синтетического мышления, смысловой памяти и
произвольного внимания,
2) Развитие навыков исследовательской деятельности
ВОСПИТАТЕЛЬНАЯ :
1) Способствовать развитию творческой деятельности
2) Развивать у учащихся коммуникативные компетенции,
потребности к самообразованию.

2 3 4 5 6

7

-7 -6 -5 -4 -3 -2 -1

7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

[-2; 4]

[-5; 6)

[-5; 5]

(-2; 4]

2

1

3

4

ПОДУМАЙ!

Это множество значений!

ПОДУМАЙ!

ВЕРНО!

Математический диктант

6 7
-7 -6 -5 -4 -3 -2

-1

7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

Функция задана графиком. Укажите множество значений этой функции.

[-5; 7]

(-5; 7)

[-3; 5]

(-3; 5)

3

1

2

4

Это область определения!

ПОДУМАЙ!

ПОДУМАЙ!

ВЕРНО!

которой изображен на рисунке, отрицательна?
х2
х3
х4
Угол наклона касательной
с

осью Ох тупой, значит k < o.

Проверка (4)

х3

х

у

х4

х2

В этой точке производная
равна нулю!

В этой точке производная равна нулю!

ПОДУМАЙ!

ПОДУМАЙ!

ПОДУМАЙ!

х1

Геометрический
смысл производной
k = tg α

Угол наклона касательной
с осью Ох острый, значит k > o

ВЕРНО!

касательная к нему в точке с абсциссой х0.
Найдите

значение производной в точке х0.

1

3

4

2

Подумай!

Подумай!

Подумай!

х0

Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох равен 0 (касательная параллельна оси Ох, значит tg00 = 0

0

1

–1

не существует

Верно!

какой точке значение производной отрицатально.
4
2
3
В этой точке производная не

существует

Верно!

Угол наклона касательной с осью Ох острый, значит k > o.

х1 х2 х3 х4

Угол наклона касательной с осью Ох тупой, значит k < 0.

1

В этой точке производная равна нулю!

х1

х2

х3

х4

-2 -1
1 2 3

4 5 х

На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку, в которой производная равна 0.

2

3

4

1

Не верно!

Не верно

Верно!

Не верно!

1

-1

1

-3

на отрезке [a;b]
На рисунке изображен ее график. В

ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.

Проверка

y = f(x)

 

y

x

2

11

8

Подумай!

Подумай!

Подумай!

Верно!

5

a

b

касательная к нему в точке с абсциссой х0.
Найдите

значение производной в точке х0.

4

2

3

1

Подумай!

Подумай!

Верно!

Подумай!

х0

Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох острый, значит k >o.
Из прямоугольного треугольника
находим tgα = 4 : 4 =1

–5

–1

5

1

касательной с осью Ох тупой, значит k < o.
Из

прямоугольного треугольника
находим tgα = 6 : 3 =2. Значит, k= -2

На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.

3

2

4

1

Подумай!

Подумай!

Верно!

Подумай!

х0

0,5

–0,5

–2

2

точки функции, максимумы и минимумы.

её производная равна нулю или не существует, называются критическими

точками этой функции.

х

у

0

х1

х2

у

х

0

х1

х2

экстремума: из того, что производная в точке х0 обращается

в нуль, необязательно следует, что в этой точке функция имеет экстремум.

Например, производная f(x) = x3 обращается в нуль в точке 0, но экстремума в этой точке функция не имеет.

х0 производная меняет знак с плюса на минус, то

точка х0 есть точка максимума.

минуса на плюс, то точка х0 есть точка минимума.

-1

1

-

+

-

х = -1 – точка минимума, х =1 – точка максимума,
f (1) = 2 , f (-1) = -2

у

х

2

-2

1

-1

288, 290