по двум углам
β
β
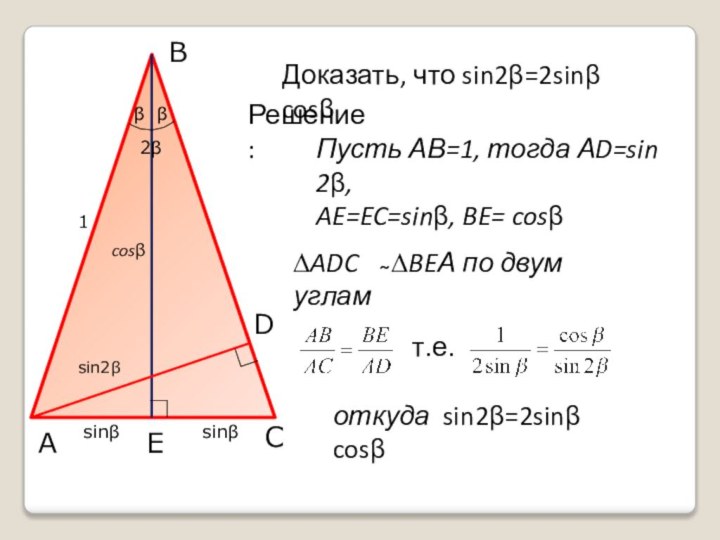
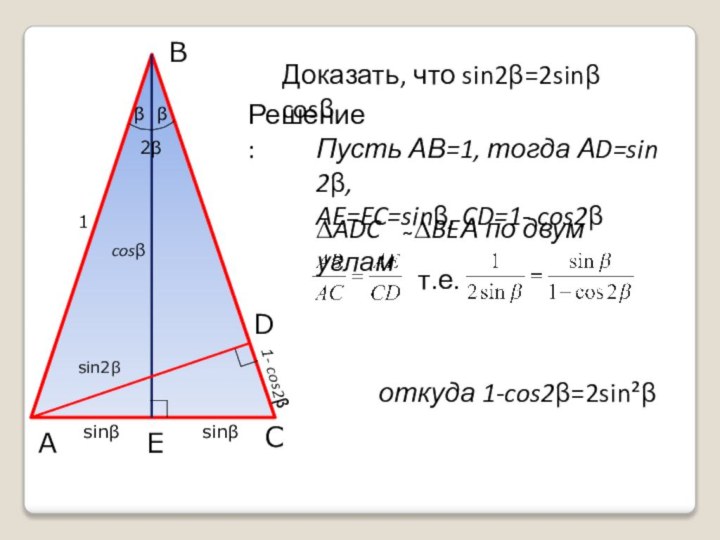
Пусть АВ=1, тогда АD=sin 2β,
AE=EC=sinβ, CD=1-
cos2β
т.е.
откуда 1-cos2β=2sin²β
1
sin2β
sinβ
sinβ
cosβ
2β
1- cos2β
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















т.е.
откуда 1-cos2β=2sin²β
1
sin2β
sinβ
sinβ
cosβ
2β
1- cos2β
1
sin2β
sinβ
sinβ
cosβ
2β
1- cos2β
Так как , то
α
β
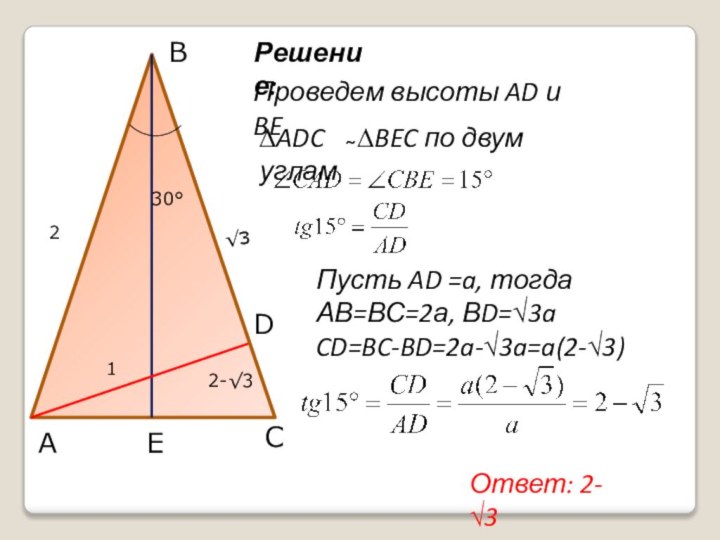
Пусть AB=c ВС =а, АС=b, и BD=h, тогда
a
b
h
c
АВ=ВС, тогда
2соs 36°=1+2cos 72°
cos36°-cos72°= 0,5
x
x
2x
2x
3x
x
Доказать тождество cos 36°-cos72°=0,5
Решение:
cos(arcctg3+arctg0,5)=√2/2
A
B
C
D
Ответ:√2/2
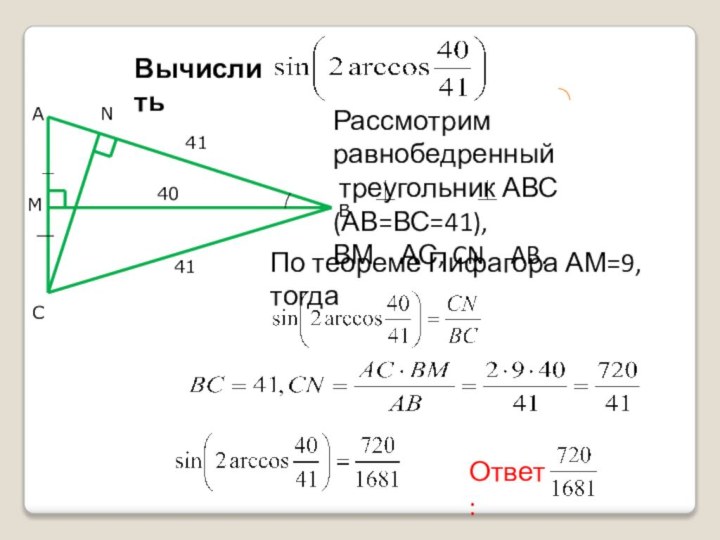
MAB = arctg3, NAC=arctg2,
а их сумма равна
Ответ: -1