- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на темуКвадратичная функция.
Содержание
- 2. Цели урока.Систематизировать и обобщить знания по теме
- 3. План урока1.Проверка домашнего задания . Презентация.2.Повторение теории
- 4. Презентация. «Парабола вокруг нас» Квадратичная
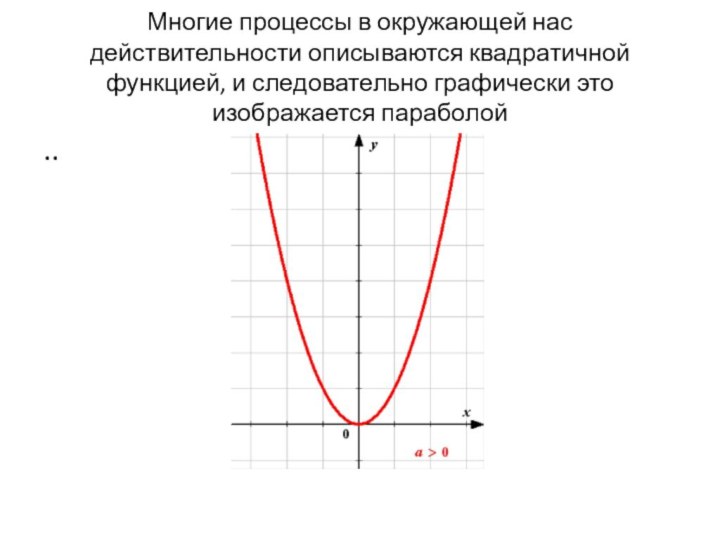
- 5. Многие процессы в окружающей нас действительности описываются квадратичной функцией, и следовательно графически это изображается параболой..
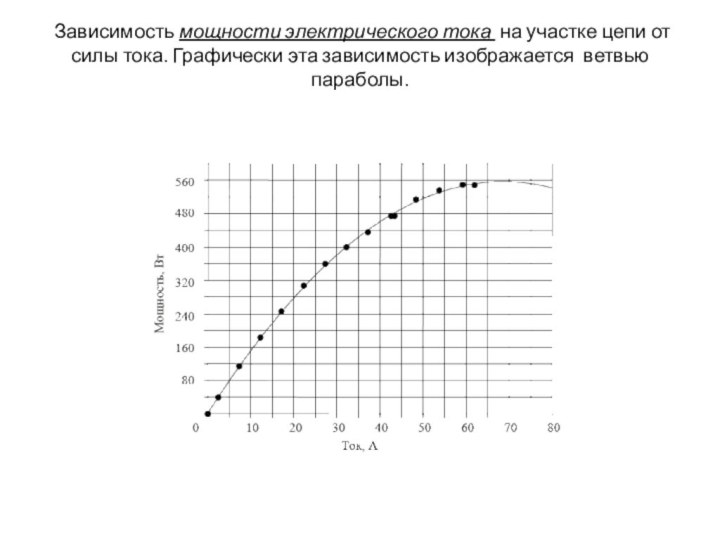
- 6. Зависимость мощности электрического тока на участке цепи
- 7. Поражают своей красотой и лёгкостью подвесные мосты.
- 8. Струя воды тоже движется по параболе.
- 9. Траектория мяча, брошенного камня, артиллерийского снаряда будет параболой
- 10. Если вращать параболу вокруг ее оси вращения
- 11. Параболоид вращения фокусирует пучок лучей, параллельный главной
- 12. , парабола обладает оптическим свойством: все лучи
- 13. Прожекторы
- 14. Автомобильные фары
- 15. Спутник вокруг земли движется по параболической орбите
- 16. Параболическая солнечная электростанция в Калифорнии, США
- 17. Парабола. Её форма невероятна, как, впрочем, и
- 18. Траектории прыжков животных близки к параболе
- 19. На мосты ли ты посмотришь, в горы
- 20. Парабола в строительстве
- 22. Здание библиотеки в Норвегии.
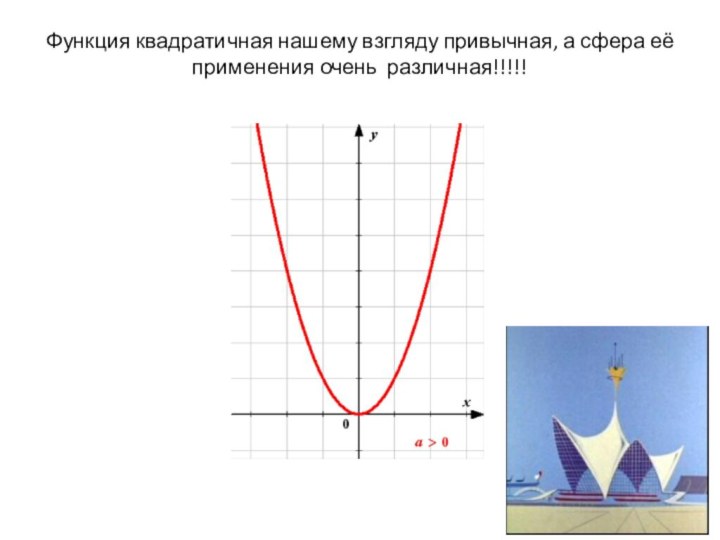
- 25. Функция квадратичная нашему взгляду привычная, а сфера её применения очень различная!!!!!
- 26. Устная работа.Вместо многоточия вставить пропущенные слова.Функция вида
- 27. Функция y = x² - это
- 28. Координаты вершины параболы y = ax² +
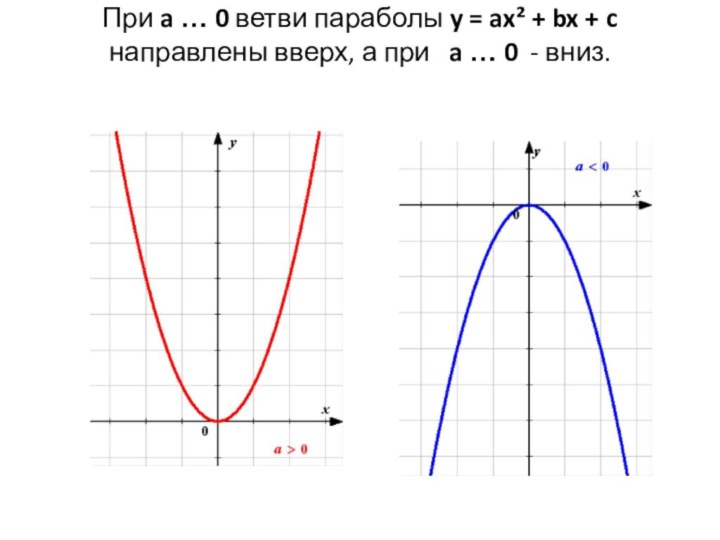
- 29. При a … 0 ветви параболы y
- 30. Определить координаты точек пересечения параболы с
- 31. Работа в группах.1.Определите , какие из
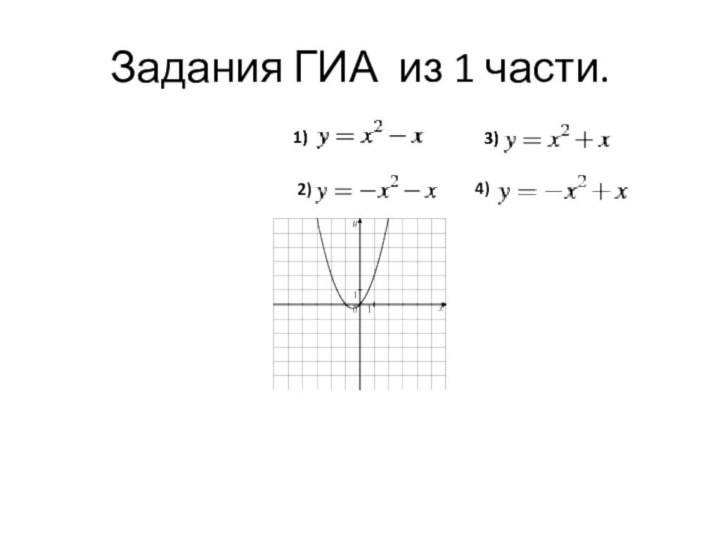
- 32. Задания ГИА из 1 части.2)4)
- 33. . График какой функции изображён на чертеже?
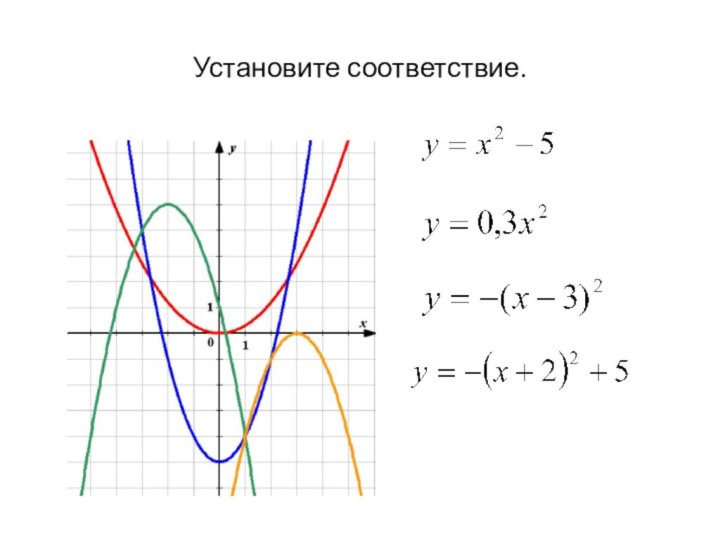
- 34. Установите соответствие.
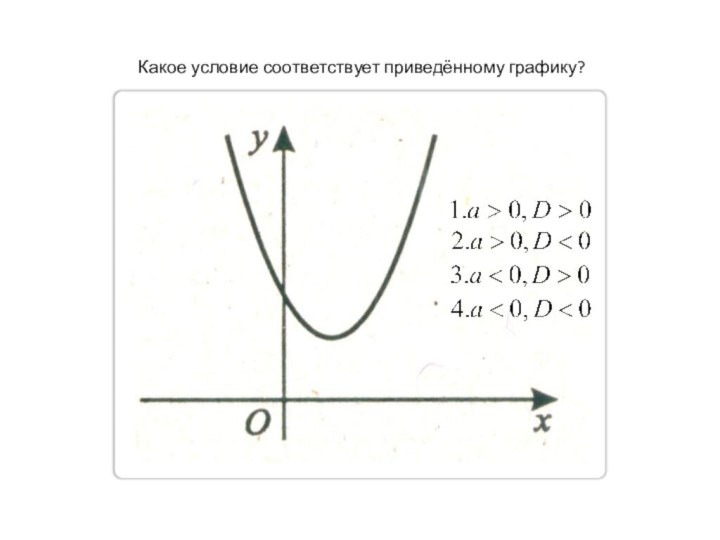
- 35. Какое условие соответствует приведённому графику?
- 36. Вычислите координаты вершины параболы у = -
- 37. По графику квадратичной функции определите знаки коэффициентов
- 38. Выбрать верное утверждение.1) квадратичная функция имеет наименьшее
- 39. Задания ГИА из 2 части.Построить график функции и ответить на вопросы.
- 40. f(х)=1.Найти D(f).2.Вычислить: f(0), f(1),
- 41. Модуль и квадратичная функция.Задача 1.По известному графику
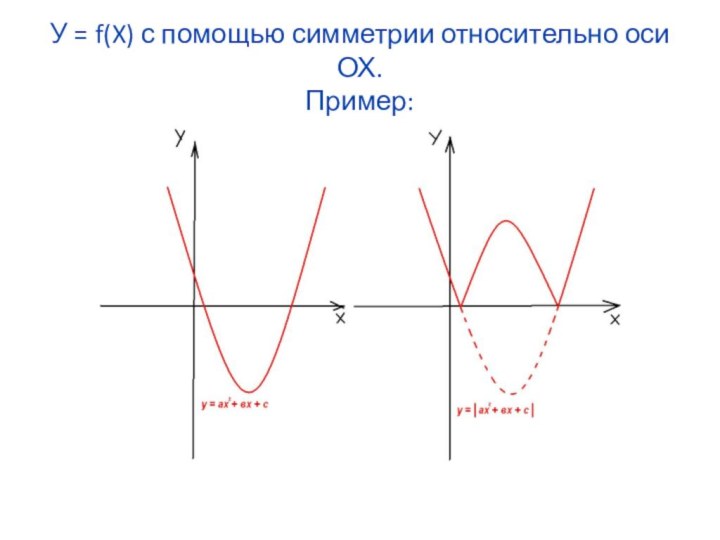
- 42. У = f(X) с помощью симметрии относительно оси ОХ. Пример:
- 43. Задача 2.По известному графику функции у
- 45. Домашнее задание.Постройте графики функций: 1.у = х²-4х
- 46. Скачать презентацию
- 47. Похожие презентации
Цели урока.Систематизировать и обобщить знания по теме «Квадратичная функция»; продолжить формирование познавательной активности, умение логически мыслить, рационально работать; способствовать развитию умения строить графики квадратичной функции, содержащие переменную под знаком модуля.


































Слайд 3
План урока
1.Проверка домашнего задания . Презентация.
2.Повторение теории по
теме урока.
3.Решение устных заданий из ГИА 1-часть .
4.Решение заданий
из 2-части ГИА.5. Углубление по теме. Презентация.
6.Тест.
7. Итоги урока.
Слайд 4
Презентация.
«Парабола вокруг нас»
Квадратичная функция - одно
из основных математических и общенаучных понятий. Оно сыграло и
поныне играет большую роль в познании реального мира.Слайд 5 Многие процессы в окружающей нас действительности описываются квадратичной
функцией, и следовательно графически это изображается параболой
..
Слайд 6 Зависимость мощности электрического тока на участке цепи от
силы тока. Графически эта зависимость изображается ветвью параболы.
Слайд 7 Поражают своей красотой и лёгкостью подвесные мосты. Мосты
держатся на тросах, которые в натянутом виде изображены параболой
и описываются квадратичной функцией.
Слайд 10 Если вращать параболу вокруг ее оси вращения то
получится поверхность, которую называют параболоидом вращения. Если сильно размешать ложечкой
воду в стакане, а потом вынуть ложечку, то поверхность воды примет форму такого параболоидаСлайд 11 Параболоид вращения фокусирует пучок лучей, параллельный главной оси,
в одну точку.
На этом принципе основаны параболические антенны.
Слайд 12 , парабола обладает оптическим свойством: все лучи исходящие
из источника света, находящегося в фокусе параболы, после отражения
оказываются направленными параллельно его оси. Это свойство используется при изготовлении телескопов .Слайд 17 Парабола. Её форма невероятна, как, впрочем, и высота.
Некоторые люди до сих пор не верят в существование этой
странной скалы.Слайд 19 На мосты ли ты посмотришь, в горы ли
поднимешь взгляд или ты в Магдональдс сходишь- сплошь параболы
стоят!
Слайд 26
Устная работа.
Вместо многоточия вставить пропущенные слова.
Функция вида
y = ax² + bx + c, где a,
b и c … числа, причём … ≠ 0, называется …функцией.x - … переменная, у … переменная или … функции.
. а –….. коэффициент (стоит при x² )
b – …… коэффициент (стоит при х )
c – …….
Слайд 27 Функция y = x² - это …
функция y = ax² + b… + c, при
a = …, b = …, c = ….Значения x, при которых квадратичная функция y (x) = 0, называются … этой функции.
Графиком квадратичной функции является …….
Слайд 28 Координаты вершины параболы y = ax² + bx
+ c можно найти по формулам:
x0 = - ― , y0 = y(x0) = a … + b … + c.Осью симметрии параболы у = ax² + bx + c служит прямая х = - …….
Слайд 30 Определить координаты точек пересечения параболы с осями
координат можно по следующей схеме:
с осью Оу:
ветвь параболы пересекает ось ОУ при х = …….с осью Ох: если у = 0, то ax² + bx + c =0 , тогда
- при D > 0, парабола пересекает ось ОХ в …….., где х1 и х2 - ………….
- при D = 0, парабола касается ось ОХ в …….., где х - ;
- при D < 0, парабола ось ОХ ……..
Слайд 31
Работа в группах.
1.Определите , какие из функций
являются квадратичными .
2. Постройте схематически графики этих функций.
3.Исследуйте на
монотонность.Слайд 33 . График какой функции изображён на чертеже? А. у
= - (х-3)2+ 1 Б. у = (х+3)2-1 В.
у = (х-1)2+3Слайд 36 Вычислите координаты вершины параболы у = - 4х2
+ 8х – 7.
а) ( - 1; - 3
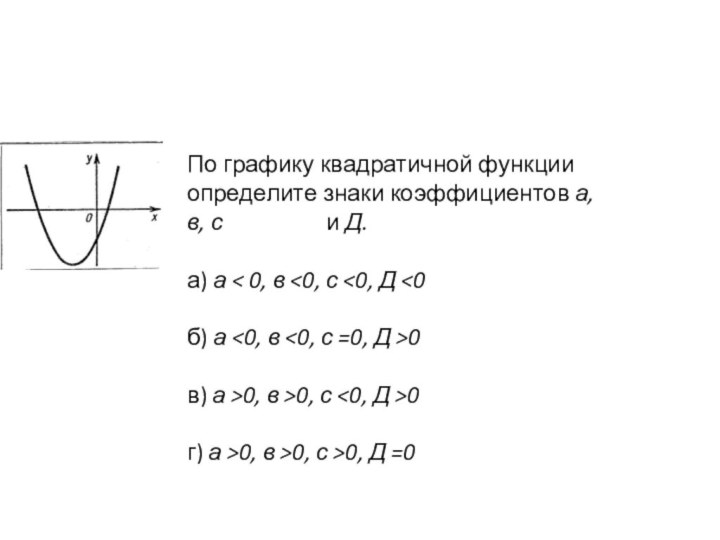
) б) ( 1; 3 ) в) ( - 1; 3 ) г) ( 1; - 3 )Слайд 37 По графику квадратичной функции определите знаки коэффициентов а,
в, с
и Д.а) а < 0, в <0, с <0, Д <0
б) а <0, в <0, с =0, Д >0
в) а >0, в >0, с <0, Д >0
г) а >0, в >0, с >0, Д =0
Слайд 38
Выбрать верное утверждение.
1) квадратичная функция имеет наименьшее значение
при а>0.
2) график квадратичной функции не пересекает ось абсцисс,
если при вычислении нулей функции Д<0.3) ось симметрии параболы – прямая, параллельная оси абсцисс
4) координата вершины параболы вычисляется по формуле у= -2а
5) нули функции, если они есть, это точки пересечения параболы с осью абсцисс
Слайд 40
f(х)=
1.Найти D(f).
2.Вычислить: f(0), f(1), f(3)
, f(7).
3 Найти E(f).
4.С помощью графика ,
определите, при каких значениях параметра m , прямая у=m имеет с графиком две общие точки.
Слайд 41
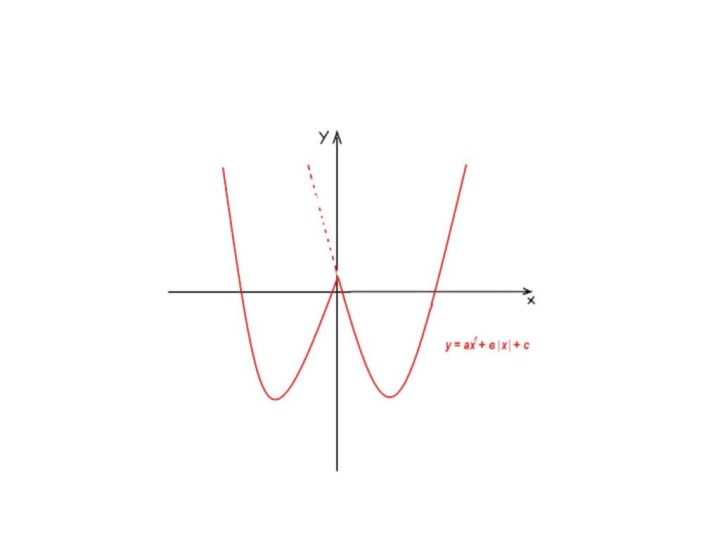
Модуль и квадратичная функция.
Задача 1.По известному графику функции
у = f(х) построить график функции у = |f(х)|.
По определению имеем: |f(X)| = f(X), если f(X)≥O,- f(X), если f(X)
Поэтому график функции у = |f(X)| совпадает с графиком функции у = f(X) на тех промежутках , где f(X) ≥ O,а на тех промежутках где f(X)





























