Презентация на тему Примеры комбинаторных задач (9 класс)

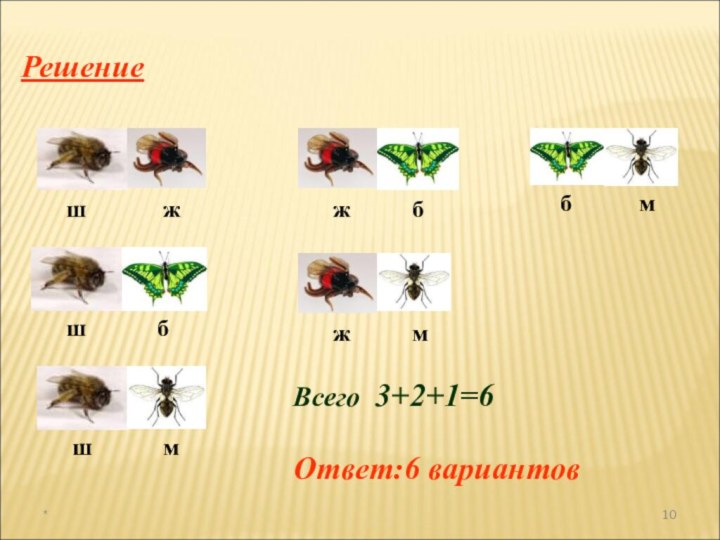
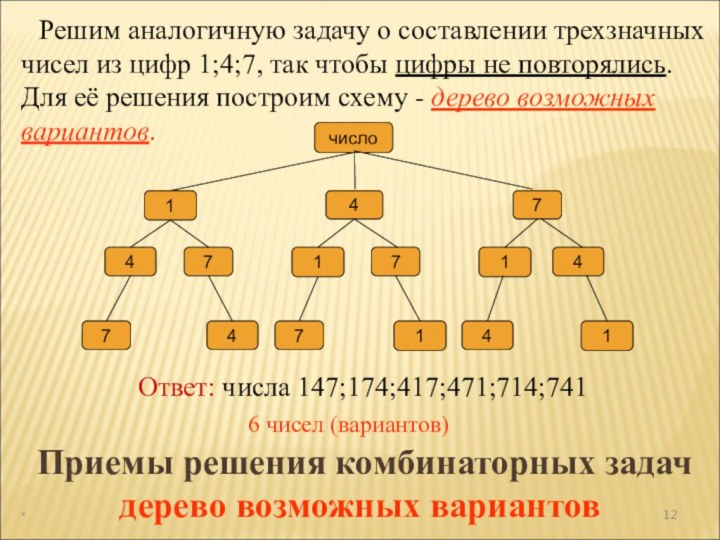
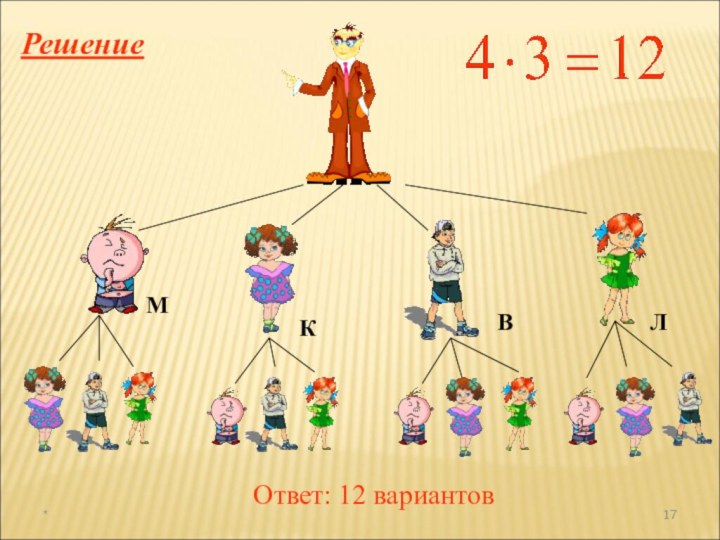
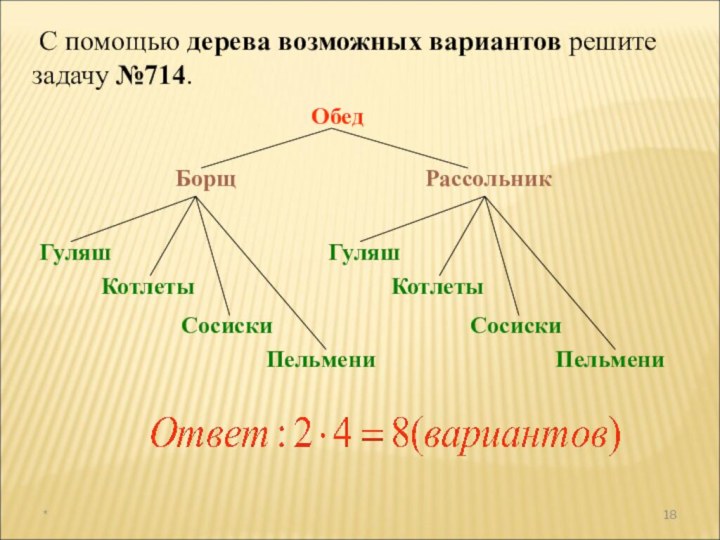
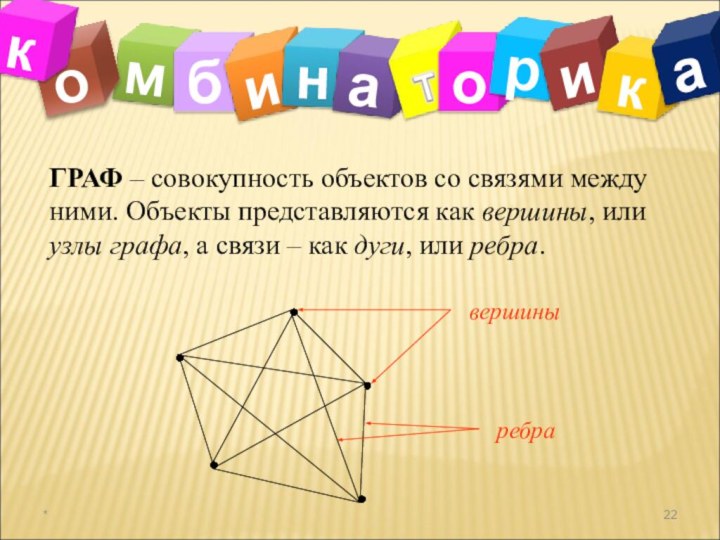
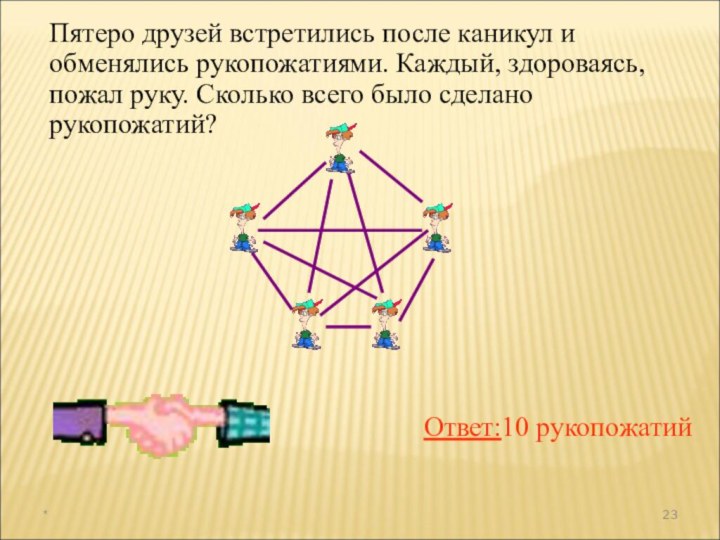
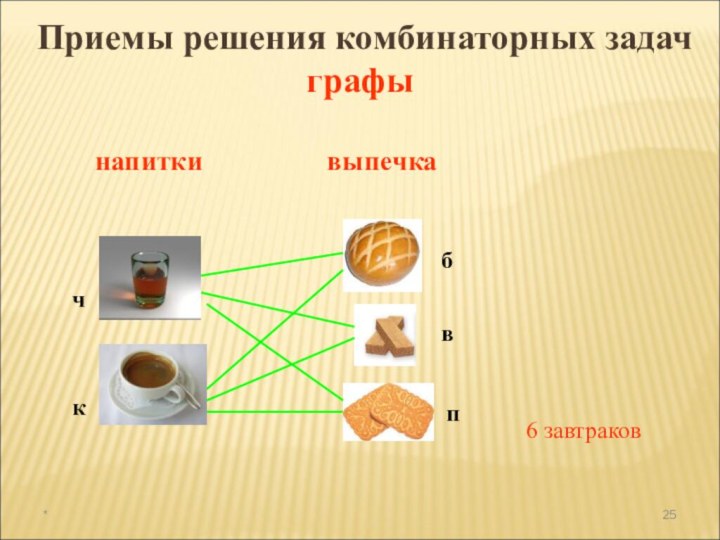
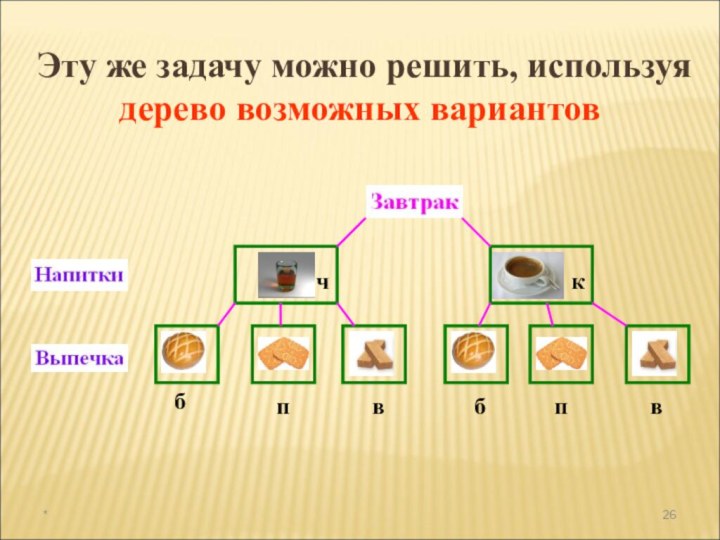
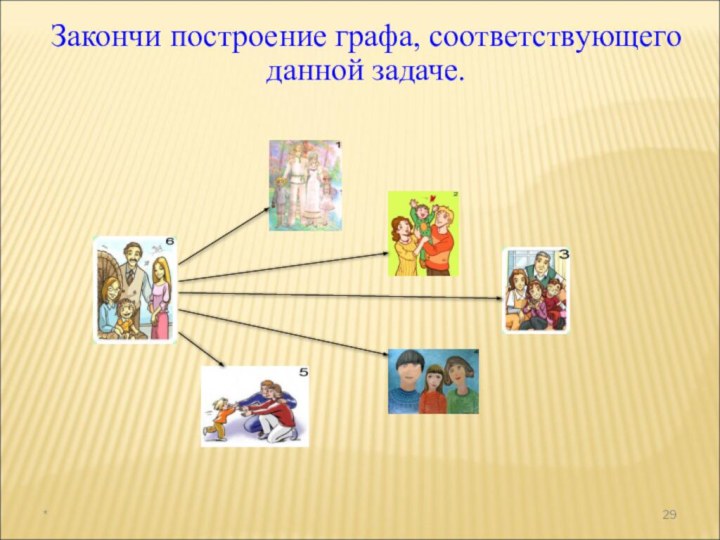
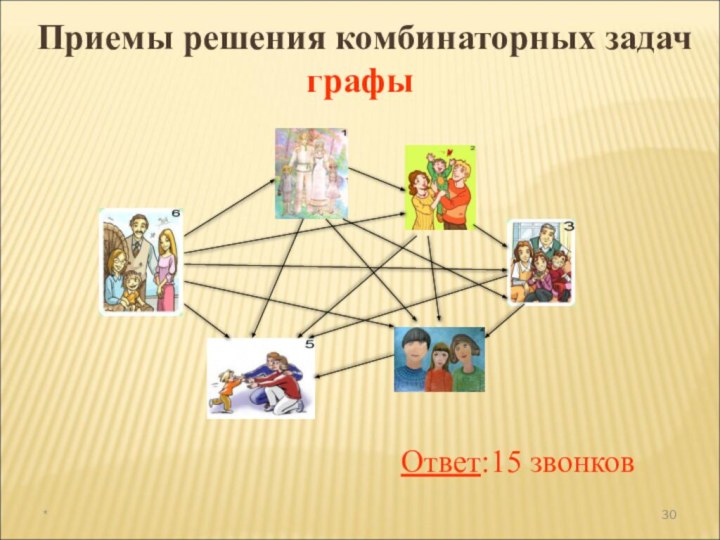
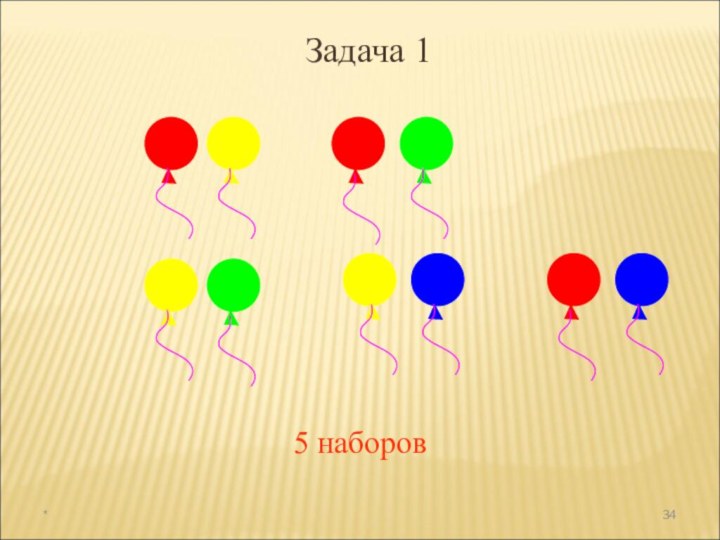
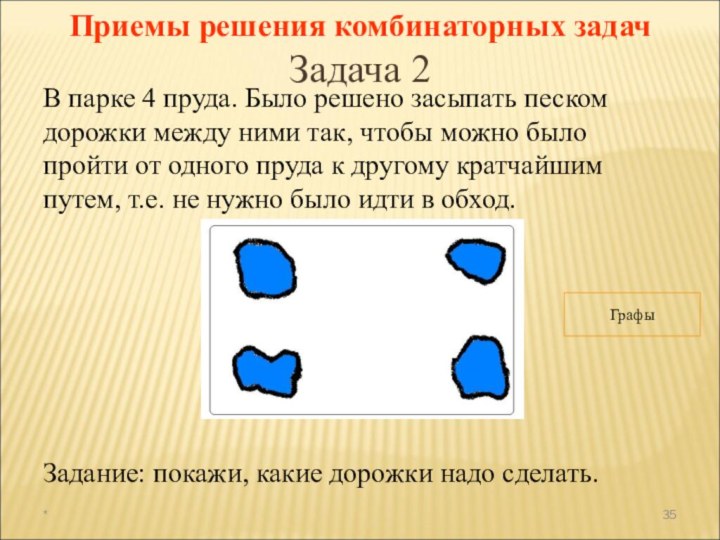
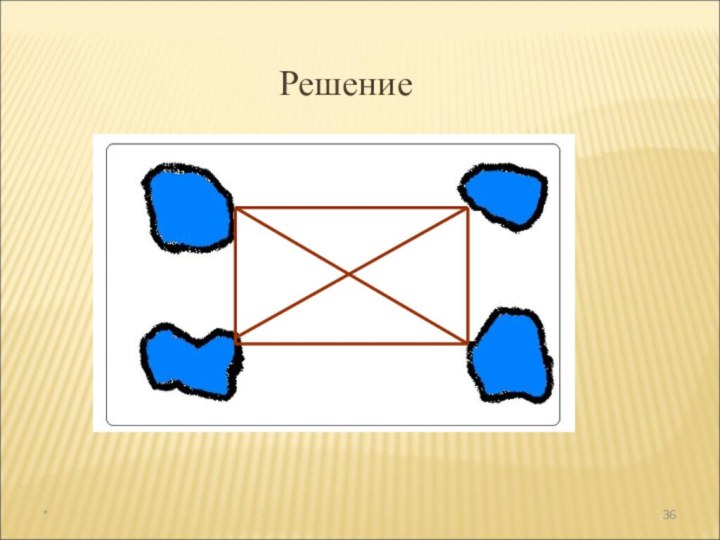
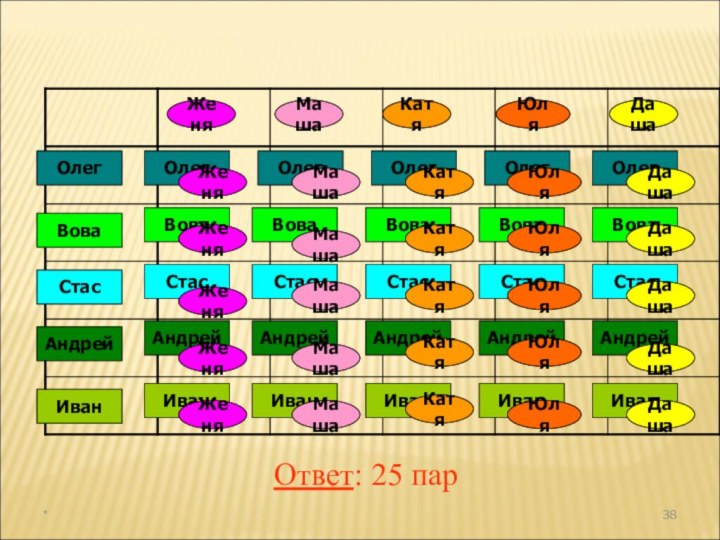
а раздел математики, в котором рассматриваются эти задачи, называют

В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций.

комбинаторикой

том, сколько различных комбинаций, подчинённых тем или иным условиям,

о

философом, математиком Лейбницем, который в 1666 году опубликовал свой

Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».

методом перебора;
решение с помощью дерева возможных вариантов;
решение

и Светлана. Она решила двух из них пригласить в

Замечание. При решении для краткости будем писать первые буквы имен.

ВЗ, ВМ, ВП, ВС
Выпишем теперь пары, в которые входит

Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.

Еще одна пара

ЗМ, ЗП, ЗС

МП, МС

ПС

Всего существует 4+3+2+1=10

Решение

Ответ:10 вариантов

Вера

Зоя

Марина

Полина

Света

Получим 4 пары.

Таких пар три.

Их две.

Далее составим пары, в которые входит Полина.

шмель, жук, бабочка и муха. Два насекомых улетели. Какие

Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.

ш

ж

б

м

Таким образом, из трёх данных цифр можно составить всего

Приемы решения комбинаторных задач метод перебора

11;14;17; (начали с 1)

Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:

Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?

41;44;47; (начали с 4)

71;74;77; (начали с 7)

Решим аналогичную задачу о составлении трехзначных чисел из

число

1

4

7

4

4

7

7

1

1

7

7

1

1

4

4

Ответ: числа 147;174;417;471;714;741

6 чисел (вариантов)

получить, не выписывая сами числа. Будем рассуждать так.

другой объект В можно выбрать k способами, то объект

Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения

удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется

Решение. 3·5 = 15

комбинаторное правило умножения

пришли четыре новых ученика Миша, Катя, Вася, Лиза. С

Л

В

К

М

№714.
Котлеты
Гуляш
Рассольник
Борщ

Пельмени

Сосиски

Котлеты

Гуляш

Пельмени

Сосиски

блокнота разного размера. Сколько различных наборов из ручки и

Приемы решения комбинаторных задач задачи, решаемые с помощью таблиц

м

с

б

с

з

ч

к

0,1,2,4,5,9?
Приемы решения комбинаторных задач задачи, решаемые с помощью

Ответ:15 чисел (5·3)

1

2

4

5

9

0

2

4

10

14

12

20

22

24

40

42

44

50

52

54

90

92

94

Объекты представляются как вершины, или узлы графа, а связи

вершины

ребра

Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий?
Ответ:10

1 вида выпечки, можно составить из чая, кофе, булочки,

Решите задачу, используя граф

ч

к

б

п

в

возможных вариантов

к месту отдыха, они поговорили друг с другом по

Решите задачу, используя граф

с помощью таблиц

(граф), 725 (таблица), 727 (умножение).
*

синие. Какие наборы можно составить из двух разных шаров?

Задачи, решаемые
методом организованного перебора

Приемы решения комбинаторных задач дополнительные задачи
Задача 1

пруда. Было решено засыпать песком дорожки между ними так,

Графы

Катя, Юля и Даша и пять мальчиков: Олег, Вова,

Приемы решения комбинаторных задач

Задачи, решаемые
с помощью таблиц

может выбрать: плюшку, бутерброд, пряник, или кекс, а запить

Ответ:12 (4·3=12)