- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение производной в физике
Содержание
- 2. В математике следует помнить не формулы, а
- 3. Урок № 1 повторительно-обобщающийПроизводная и ее применение при решении задач
- 4. Цели урока:Образовательные:Углубление понимания сущности производной путем применения ее для получения новых знаний;Установление межпредметных связей;
- 5. Воспитательные:Воспитание познавательного интереса к учебному предметуВоспитание у учащихся культуры мышления;
- 6. Развивающие :Формирование умений строить логическую цепочку рассуждений;Формирование
- 7. План урока: 1. Сведения из истории математики.2.
- 8. 1234567
- 9. Лагранж Жозеф Луи (1736 – 1813)
- 10. План исследования функции:1) Область определения функции;2) Четность
- 11. 5) Промежутки возрастания и убывания;6) Точки экстремума
- 12. Исследование функции
- 13. ЗадачаИсследуйте функцию и постройте её график:f(x)=6(x-1)x2 +3
- 14. Нули функции1xy-2
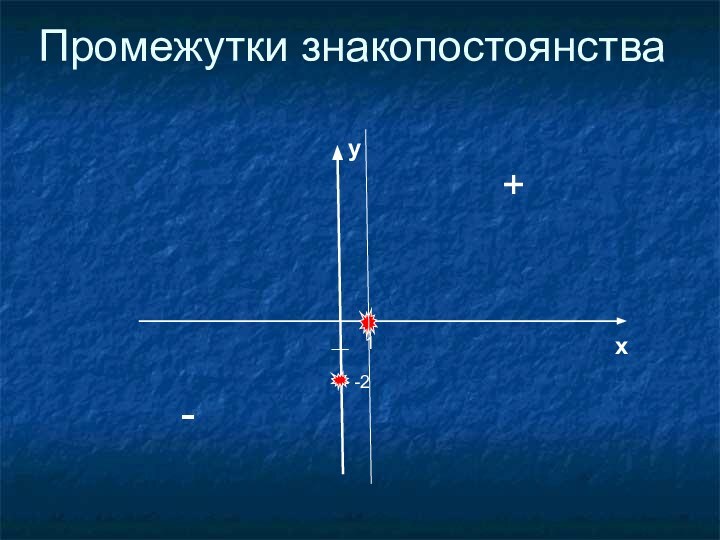
- 15. Промежутки знакопостоянства1xy-2+-
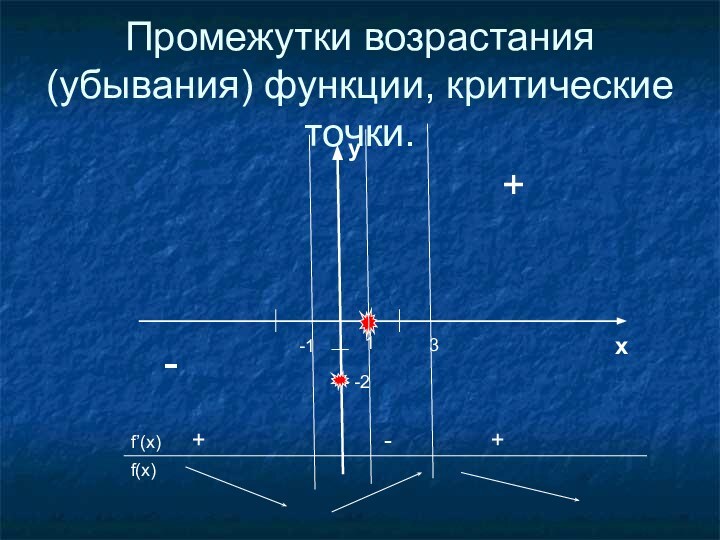
- 16. Промежутки возрастания (убывания) функции, критические точки.1xy-2+-3-1f’(x)f(x)+-+
- 18. 1xy-23-1-31
- 19. Схема применения метода поиска наибольших и
- 20. 3) Выясняется, какой практический смысл( в терминах первоначальной задачи) имеет полученный результат (на языке функций).
- 21. Задача .Площадь прямоугольника 64 см2. Какую длину
- 22. Применение производной в физике
- 23. Механическое движение
- 24. Уравнение, описывающее движение телаX = x 0
- 25. Производная от координаты по времени есть скорость.
- 26. Производная от скорости по времени есть ускорение
- 28. Решение: 1. ט (t)=x’=(-270+12t)’=
- 29. Задача №2 Дано: x(t) = - 5t
- 30. Решение:ט(t)=x’=(-5t3)’+(2t2)’+(5t)’= -15t2+2*2t+5*1 =>
- 31. a(t)=ט’=(-5t2)’+(4t)’+(5)’=
- 32. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
- 33. Гармонические колебания-это колебания, происходящие по закону sin или cos.
- 34. X(t)= xmax * sin(w*t+φ0)
- 35. xmax –амплитуда колебаний,[м]φ - начальная фаза колебаний[1цикл=2π
- 36. Определить по графику период, амплитуду и частоту колебаний. Найти максимальную силу, действующую на тело массой 150г.Задача
- 37. Решение
- 38. а =V’=(2πcos5πt)’== -2π5πsin5πt = -98,6sin5πtгде amax= -98,6
- 39. Формулы из физики и экономики, где используется
- 40. ω(t) = φ' (t) - угловая скоростьа(t)
- 41. Скачать презентацию
- 42. Похожие презентации
В математике следует помнить не формулы, а процессы мышления. В.П. Ермаков
































![Применение производной в физике xmax –амплитуда колебаний,[м]φ - начальная фаза колебаний[1цикл=2π рад.=360 °]ω- циклическая частота[Гц]φ0 –начальная](/img/tmb/11/1051069/155d64bb40ddd2d71357120e40936870-720x.jpg)






Слайд 4
Цели урока:
Образовательные:
Углубление понимания сущности производной путем применения ее
для получения новых знаний;
Установление межпредметных связей;
Слайд 5
Воспитательные:
Воспитание познавательного интереса к учебному предмету
Воспитание у учащихся
культуры мышления;
Слайд 6
Развивающие :
Формирование умений строить логическую цепочку рассуждений;
Формирование умений
проводить обобщение, переносить знания в новую ситуацию;
Развитие монологической речи
в ходе объяснений, обоснований выполняемых действий
Слайд 7
План урока:
1. Сведения из истории математики.
2. Применение производной
к исследованию функции.
3. Применение производной в решении прикладных задач.
4.
Применение производной в решении задач на уроках физики.
Слайд 10
План исследования функции:
1) Область определения функции;
2) Четность или
нечетность функции, периодичность;
3) Точки пересечения графика с осями координат;
4)
Промежутки знакопостоянства;
Слайд 11
5) Промежутки возрастания и убывания;
6) Точки экстремума и
значения; функции в этих точках;
7) Исследуют поведение функции в
окрестностях «особых» точек и при больших по модулю x;8) Построение графика функции.
Слайд 19 Схема применения метода поиска наибольших и наименьших значений
функции при решении прикладных задач:
1) Задача «переводится» на язык
функций;2)Средствами анализа ищется наибольшее или наименьшее значение этой функции на некотором промежутке;
Слайд 20
3) Выясняется, какой практический смысл( в терминах первоначальной
задачи) имеет полученный результат (на языке функций).
Слайд 21
Задача .
Площадь прямоугольника 64 см2.
Какую длину должны
иметь его стороны, чтобы периметр был наименьшим?
a
b
S=64cм2
P- наименьший
Найти:
a
и b?
Слайд 26
Производная от скорости по времени есть ускорение
а = ט/(t ) = X // (t )
(т.е
вторая производная от координаты по времени).
Слайд 30
Решение:
ט(t)=x’=(-5t3)’+(2t2)’+(5t)’=
-15t2+2*2t+5*1 =>
ט(t)=-15t2+4t+5
(уравнение, описывающее
скорость движения тела).Если t=0, то ט(0)=5 м/с
t=1с, то
ט(1)=-15+4+5=-9 м/с
Слайд 31
a(t)=ט’=(-5t2)’+(4t)’+(5)’=
-30t+ 4
a(t)=-30t+ 4
(уравнение, описывающее ускорение тела)
Если t=0 c, то a(0)=4 м/c2
t=1 с, то
а(1)=-30+4=-26 м/c2
Слайд 35
xmax –амплитуда колебаний,[м]
φ - начальная фаза колебаний[1цикл=2π рад.=360
°]
ω- циклическая частота[Гц]
φ0 –начальная фаза колебаний
t- время колебаний[с]
∏ ≈ 3,14T-период колебаний[с]
ω
Слайд 36 Определить по графику период, амплитуду и частоту колебаний.
Найти максимальную силу, действующую на тело массой 150г.
Задача
Слайд 37
Решение
Из графика:
xmax= 0,4(м); Т=0,4(с); φ0=0.ν = 1/Т = 1/0,4 = 2,5(с-1)
Х= 0,4sin(2π*2,5t) = 0,4sin5πt
V= x’= (0,4sin5πt)’= 2πcos5πt,
где Vmax = 2π = 6,28 (м/с)
Слайд 38
а =V’=(2πcos5πt)’=
= -2π5πsin5πt = -98,6sin5πt
где amax= -98,6 м/с2-амплитуда
ускорения
F = m•amax
F = 0,15*(-98,6)= -14,8 [H]
Ответ: xmax= 0,4(м);
Т=0,4(с);ν=2,5с-1; F = -14,8 [H].
Слайд 39
Формулы из физики и экономики, где используется производная:
υ(t)
= х' (t) – скорость
a(t) = υ'(t) -
ускорениеJ(t) = q'(t) - сила тока
C(t) = Q' (t) - теплоемкость
d(l) =m' (l) - линейная плотность
K(t) = l' (t) - коэффициент линейного расширения
Слайд 40
ω(t) = φ' (t) - угловая скорость
а(t) =
ω' (t) - угловое ускорение
N(t) = A'(t) - мощность
П(t)
= υ ' (t) - производительность труда,где υ (t) - объем продукции
J(x) = y ' (x) - предельные издержки производства,
где y – издержки производства в зависимости от объема выпускаемой продукции x.