Слайд 2
Содержание
Введение
Понятие векторно-координатного метода
Проблемы при использовании координатного метода
Понятие системы
координат
Декартова система координат на плоскости
Декартова система координат в пространстве
Введение
системы координат в заданиях C2
Координаты куба
Координаты трехгранной призмы
Координаты шестигранной призмы
Координаты четырехугольной пирамиды
Применение векторно-координатного метода при решении геометрических задач в заданиях С2
Расстояние между двумя точками
Расстояние от точки до прямой
Расстояние от точки до плоскости
Расстояние между скрещивающимися прямыми
Угол между двумя прямыми
Угол между прямой и плоскостью
Угол между плоскостями
Уравнение плоскости, проходящей через три точки
Примеры решения задач векторно-координатным способом
Заключение
Список использованной литературы
Слайд 3
Введение
В геометрии применяются различные методы решения задач –

это синтетический (чисто геометрический) метод, метод преобразований, векторно-координатный метод,
метод ключевых задач. Также методы делятся на методы алгебры и геометрии.
Геометрические методы: метод треугольников, метод площадей, метод вспомогательных фигур, координатный метод, векторный метод и др. Они занимают различное положение в школе.
Основным методом считается синтетический, а из других наиболее высокое положение занимает векторно-координатный метод потому, что он тесно связан с геометрией.
Изящество синтетического метода достигается с помощью интуиции, догадок, дополнительных построений. Векторно-координатный метод этого не требует: решение задач во многом алгоритмизировано, что в большинстве случаев упрощает поиск и само решение задачи. Координатный метод решения задач на сегодняшний день самый мощный и при правильном подходе позволяет решить фактически все виды математический, физических, астрономических, и технических задач. Кроме того, координатный метод в рамках школьной программы используется достаточно ограниченно и неполно.
Слайд 4
Понятие векторно-координатного метода
Векторные приемы изучаются в школе в

весьма ограниченном количестве. В базовый учебник стереометрии Л.С. Атанасяна
включен целый параграф «скалярное произведение векторов» и даже отдельно рассматривается нахождение углов между объектами. Однако дальше темы «вычисление угла между прямыми» и осторожного намека на аналогичный алгоритм для прямой и плоскости материал не рассматривается. И даже не вводится такое понятие, как «нормаль».
Как правило учитель выбирает одну из трех стратегий подготовки к задаче С2 на ЕГЭ:
1) Полный отказ от векторных приемов
2) Изучение отдельных алгоритмов
3) Демонстрация всех приемов (без доказательств) для самых сильных учеников.
Координатный метод позволяет рассматривать множество самых трудных задач на вычисление всех видов углов (между прямыми, между прямой и плоскостью, между плоскостями) и любых расстояний (от точки до плоскости, между параллельными плоскостями, между скрещивающимися прямыми). С тремя последними работать сложнее всего, ибо приходится затрагивать тему «уравнение плоскости», «смешанное и векторное произведение векторов». К тому же аккуратный вывод самих формул заставляет прилично углубиться в теорию, без которой добиться 100%-го понимания будет невозможно.
При работе в координатах со средним по силе учеником, учебный план включает в себя работу только с алгоритмами поиска углов..
Преимущество методов аналитической геометрии перед альтернативным решением средствами дополнительных построений состоит в том, что удается полностью отстраниться от чертежа и заниматься исключительно числами (координатами). Поэтому в определенных условиях подготовки к ЕГЭ по математике удается натаскать ученика на стандартные решения. Причем за весьма короткий срок и в обход большого количества тем.
Если у школьника имеются серьезные проблемы с пониманием определений, с чтением или построением сложного стереометрического рисунка, если ему никак не удается подобрать необходимые дополнительные построения, то можно построить работу по С2 на векторах. Особенно это актуально в условиях экстренной помощи, когда на подготовку к ЕГЭ отводится всего лишь 2-3 месяца. Если у преподавателя нет времени на неспешный комплексный подход, то лучше все го сразу обратиться к координатам.
Слайд 5
Проблемы при использовании координатного метода
Три проблемы координатного метода:
О

каких проблемных ситуациях необходимо помнить? Какие ошибки чаще всего
допускаются школьниками?
1) От того, что забывают алгоритм поиска нормали
2) Путаются с введением системы координат или с определением координат у точек (задающих прямые и плоскости) в разных многогранниках.
3) Не справляются с вычислениями, если в координаты вершин попадают квадратные корни. Обычно эта ситуация возникает в треугольных пирамидах .
Именно поэтому отдельно останавливается на этих компонентах. Третью проблему снять не удается. Пирамиду не переделаешь. А вот получить практику нахождения нормали и научиться определять координаты вполне реально.
Какую подготовку к восприятию векторных приемов проводит учитель?
Необходимо повторить следующие темы:
1) Координаты точки и координаты вектора
2) Длина вектора
3) скалярное произведение векторов
4) координаты середины отрезка (на случай, если плоскость или прямая будут заданы серединами каких-нибудь диагоналей или ребер у пирамид).
Как и в других темах у меня есть свои приемы для запоминания формул. Какие формулы тяжелее всего запомнить? Те, которые нужно учить целыми блоками, которые в целом схожи друг с другом, но расходятся в мелочах. Вот эти мелочи из головы как раз и выпадают, ибо тонут в общей массе знаков.
Слайд 6
Понятие системы координат
Система координат — комплекс определений, реализующий метод
координат, то есть способ определять положение точки или тела
с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Рене Декарт является одним из создателей аналитической геометрии (которую он разрабатывал одновременно с Пьером Ферма), позволявшей алгебраизировать эту науку с помощью метода координат. Предложенная им система координат получила его имя.
Слайд 7
Декартова система координат на плоскости
Декартова система координат хорошо
известна. И всё же сформулируем подробнее, каким образом она
задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.
Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x, y).
Слайд 8
Декартова система координат в пространстве
Декартовы координаты в пространстве
задаются с помощью точки начала координат и трёх взаимно-перпендикулярных
направленных прямых.
Прямые занумерованы, задан единичный отрезок.
Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
Слайд 9
Введение системы координат в заданиях C2
Метод координат — это
довольно лёгкий способ, но в настоящих задачах C2 никаких координат и векторов
нет. Поэтому их придется вводить: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, решив некоторые задачи, мы пришли к выводу, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Слайд 10
Координаты куба
Это самый простой многогранник, все двугранные углы
которого равны 90°.
Система координат также вводится очень просто:
Начало координат — в точке A;
Чаще
всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Слайд 11
Итак, теперь у каждой вершины куба есть координаты. Соберем их
в таблицу — отдельно для нижней плоскости куба:
И для верхней:
Несложно заметить, что точки верхней
плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1).
Слайд 12
Координаты трехгранной призмы
При правильном подходе достаточно знать координаты только
нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные
трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба.
Вводим систему координат:
Начало координат — в точке A;
Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Слайд 13
Получаем следующие координаты точек:
Как видим, точки верхнего основания
призмы снова отличаются от соответствующих точек нижнего лишь координатой z.
Основная проблема — это точки C и C1. У них есть иррациональные координаты, и для того чтобы довольно просто решить задание С2 эти иррациональные координаты надо просто запомнить. Ну, или понять, откуда они возникают.
Слайд 14
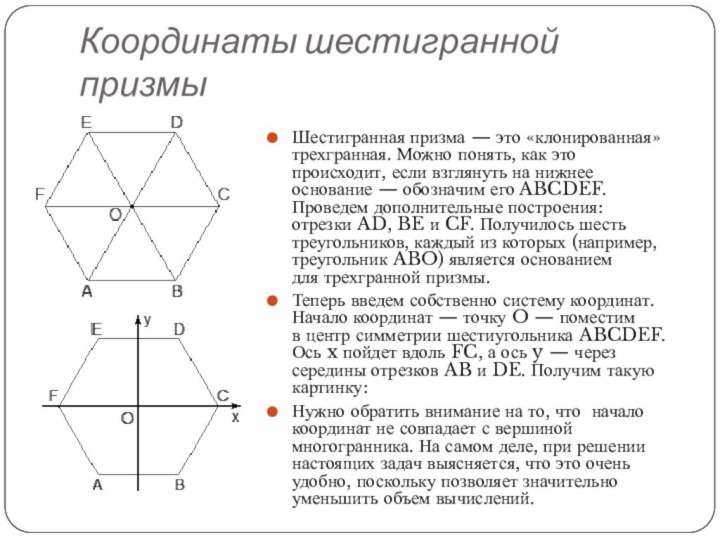
Координаты шестигранной призмы
Шестигранная призма — это «клонированная» трехгранная. Можно
понять, как это происходит, если взглянуть на нижнее основание — обозначим его
ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Нужно обратить внимание на то, что начало координат не совпадает с вершиной многогранника. На самом деле, при решении настоящих задач выясняется, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Слайд 15
Нужно обратить внимание на то, что начало координат
не совпадает с вершиной многогранника. На самом деле, при решении настоящих
задач выясняется, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку (см. рис.)
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
Слайд 16
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сложно, поэтому
я разобрала только самый простой случай — правильную четырехугольную пирамиду,
все ребра которой равны единице.
Итак, правильная четырехугольная пирамида. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY.
Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Слайд 17
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY.
Здесь все просто: в основании лежит квадрат, его координаты известны.
Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Слайд 18
Применение векторно-координатного метода при решении геометрических задач в
заданиях С2
В задании С2 по математике чаще всего
надо решить задачу, в которой надо определить:
Расстояние между двумя точками
Расстояние от точки до прямой
Расстояние от точки до плоскости
Расстояние между скрещивающимися прямыми
Угол между двумя прямыми
Угол между прямой и плоскостью
Угол между плоскостями
Задачи элементарные, если следовать алгоритму решения С2 и помнить про основные тригонометрические свойства, как например свойства диагоналей или площадь поверхности многогранника. Опорные задачи вам помогут вспомнить эти основные свойства.
Теперь перейдем непосредственно к алгоритмам.
Слайд 19
Расстояние между двумя точками
Для определения расстояния между двумя
точками А и В используем один из двух способов:
Включаем
АВ в некоторый треугольник и находим его длину как сторону треугольника
По формуле
При чем координатный метод на мой взгляд наиболее прост, надо только аккуратно определить координаты каждой точки.
Слайд 20
Расстояние от точки до прямой
Для определения расстояния от
точки до прямой вычисляется
как длина отрезка перпендикуляра, если удастся
включить этот отрезок в некоторый треугольник в качестве одной из высот
при помощи координатного метода используя формулы вычисления площади, в которых искомым расстоянием будет высота и
Еще один способ:
Пусть l – данная прямая с направляющим вектором , M – данная точка, N – ее проекция на прямую l, тогда – искомое расстояние.
Если А – произвольная точка прямой l, то в прямоугольном треугольнике MNA гипотенуза MA и катет могут быть найдены. Значит,
Слайд 21
Расстояние от точки до плоскости
Пусть α – данная
плоскость с нормальным вектором , M –
данная точка,
d – расстояние от точки М до плоскости α.
Если N – произвольная точка плоскости α, а M1 и N1 – проекции точек M и N на ось то
Слайд 22
Также расстояние от точки до плоскости равно
длине перпендикуляра,
опущенного из этой точки на плоскость. Для этого аккуратно
строим сечение, которое перпендикулярно плоскости и проходит через заданную точку. Искомое расстояние будет равно высоте полученного нового многогранника.
С использованием координатного метода
Уравнение находится путем подстановки координат трех точек, принадлежащих этой плоскости
С использованием векторного метода
Для этого надо вспомнить правила сложения и вычитания векторов, что произведение перпендикулярных векторов равно нулю.
Методом объемов, если имеется пирамида АВСМ, то расстояние от точки М до плоскости, содержащей треугольник АВС вычисляется по формуле
Методом опорных задач
Слайд 23
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми можно
решить с помощью
Поэтапно-вычислительного метода:
построить общий перпендикуляр двух скрещивающихся прямых
и найти его длину;
построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстоянию от точки до прямой, построенной в плоскости;
заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, найти расстояние между этими плоскостями
построить плоскость, перпендикулярную одной из этих прямых и построить ортогональную проекцию второй прямой
Слайд 24
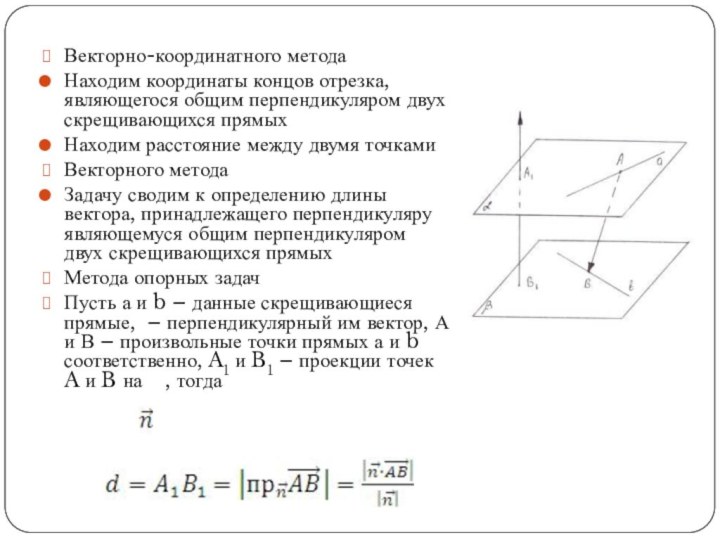
Векторно-координатного метода
Находим координаты концов отрезка, являющегося общим перпендикуляром
двух скрещивающихся прямых
Находим расстояние между двумя точками
Векторного метода
Задачу сводим
к определению длины вектора, принадлежащего перпендикуляру являющемуся общим перпендикуляром двух скрещивающихся прямых
Метода опорных задач
Пусть а и b – данные скрещивающиеся прямые, – перпендикулярный им вектор, А и В – произвольные точки прямых а и b соответственно, A1 и B1 – проекции точек A и B на , тогда
Слайд 25
Угол между двумя прямыми
Угол между двумя прямыми определяется
несколькими способами
Поэтапно-вычислительным методом
При этом надо достроить до треугольника, в
котором одна из сторон является той, расстояние от которой находится (с), а вторая сторона (в) параллельна скрещивающейся прямой
Векторно-координатный метод
Используют формулу или
где векторы p и q параллельны заданным прямым, определены их координаты
Метод опорных задач
Слайд 26
Угол между прямой и плоскостью
Угол между прямой и
плоскостью определяется путем включения его в прямоугольный треугольник в
качестве одного из острых углов, либо векторно-координатным методом или
Либо методом опорных задач
Слайд 27
Пусть – направляющий вектор данной прямой l,
– нормальный вектор данной плоскости α, l1 –
проекция прямой l на плоскость α .
Как известно, угол φ между прямой l и ее проекцией l1 на плоскость α называется углом между прямой и плоскостью. Имеем
Слайд 28
Угол между плоскостями
Угол между плоскостями – это угол,
образованный полуплоскостями. Его величина измеряется величиной линейного угла, получаемого
при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Векторно-координатный алгоритм решения задач, в которых необходимо найти угол между плоскостями:
Использование векторов нормалей пересекающихся плоскостей. Используют формулу или где векторы p и q параллельны заданным прямым, определены их координаты
Использование направляющих векторов скрещивающихся прямых
Слайд 29
Уравнение плоскости, проходящей через три точки
Теорема. Пусть даны
координаты трех точек, через которые надо провести плоскость: M
= (x1, y1, z1); N = (x2, y2, z2); K = (x3, y3, z3). Тогда уравнение этой плоскости можно записать через определитель:
Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2.
Задача. Составьте уравнение плоскости, проходящей через точки: A1 = (0, 0, 1); B = (1, 0, 0); C1 = (1, 1, 1).
Составляем определитель и приравниваем его к нулю:
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
При расчете числа d мы преобразовали уравнение, чтобы переменные x, y и z шли в правильной последовательности, а переменная x со знаком «+». Уравнение плоскости готово!
Слайд 30
Примеры решения задач векторно-координатным способом
Задание 1
Ребро куба ABCDA1B1C1D1
имеет длину а. На диагоналях D1A и A1B лежат
соответственно точки М и К так, что D1M:D1A=KB:A1B=1:3. Найдите расстояние от вершины С до прямой МК.
Выберем прямоугольную декартову систему координат так, как указано на рисунке.
Относительно выбранной системы координат имеем:
Найдем расстояние от точки C до прямой MK.
Пусть N – ортогональная проекция точки C на прямую MK. Тогда
По теореме Пифагора из находим
Ответ:
Слайд 31
Задание 2
В единичном кубе A…D1 найти расстояние между
прямыми AB1 и BD.
Решение. Так как DC1 || AB1,
то BDC1 || AB1. Поэтому расстояние
ρ(AB1; BD) = ρ(AB1; BDC1) = ρ(A; BDC1).
Введем систему координат, как показано на рисунке, и определим координаты точек: A(0; 0; 0), B(0; 1; 0), D(1; 0; 0), C1(1; 1; 1;).
Запишем уравнение плоскости DBC1
Отсюда b = -d, a = -d и c = d. Уравнение плоскости через точки B, D, C1, имеет вид -dx - dy + dz + d = 0, или x + y - z - 1 = 0 после сокращения на
Расстояние между прямыми AB1и BD равно
Ответ:
Слайд 32
Задание 3
В правильной шестиугольной призме A…F1, ребра которой
равны 1, найдите угол между прямыми AB1 и BF1.
Решение.
Введем прямоугольную систему координат, как указано на рисунке
F1(-1; 0; 1)
Отсюда
где φ — искомый угол
Ответ:
Слайд 33
Заключение
Проанализировав задания С2 и их решения, можно сделать

вывод что метод координат является наиболее удобным для решения.
Но у этого метода есть некоторые недостатки: приходится делать громоздкие вычисления и могут возникнуть проблемы с оформлением. Не смотря на это, метод координат показался мне намного удобнее других методов.
Таким образом, векторно-координатный метод в целом достаточно прост для восприятия и применения на практике. Основная проблема состоит в том, что для его применения необходимо помнить формулы, которые, как показывает практика, часто «вылетают» из памяти.
Как справиться с проблемой заучивания? Почему школьники забывают формулы? Не только потому, что мало решают задачи. Сложно запомнить сразу несколько формул, которые к тому же еще и похожи друг на друга. Практика показывает, что школьники совершенно не умеют отслеживать отличия и взаимосвязи в содержании с теми объектами или процессами, которые формулы описывают. Необходимо учить школьников искать эти особенности — маленькие зацепочки, при помощи которых можно быстрого и легко запомнить состав функций, знаков, операций.
Формулы для нахождения углов по координатам — не исключение. Ученику сложно запомнить, с какой функции каждая их них начинается? Если обратить его внимание на участие в каждой из них косинуса (он занимается непосредственным вычислением), то это поможет запомнить среднее звено. Как вспомнить функцию, с которой формула начинается? Заметим, что если объекты, между которыми ищется угол, — разного вида (плоскость и прямая), то и тригонометрические функции будут разного вида (включаем ассоциативную память), а если одного вида (две прямые или две плоскости), то и функций будут одного вида. Поскольку косинус закрепелен «намертво», то при «разных» начинаем с синуса, а при «равных» с этого же косинуса. Очень просто запоминается. Кроме этой закономерности неплохо было бы выделить общий характер формул: синус/косинус угла между объектами равен модулю косинуса угла между их заменителями. Заменителем прямой является направляющий вектор, а заменителем плоскости — ее нормаль (любая).
Правильная подготовка к ЕГЭ по математике включает в себя обязательную практику решения задач методом координат. Большинство учащихся решают задачи С2 именно координатно-векторным методом или используют его для проверки полученного решения.