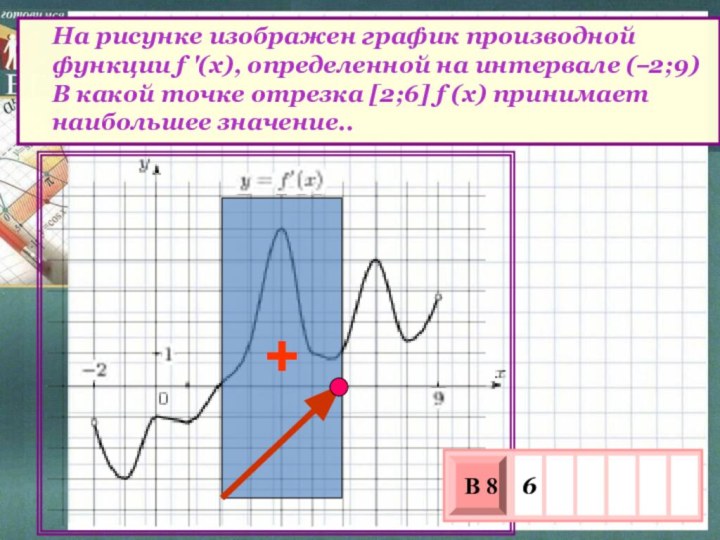
f (x), определенной на интервале (–5;5) Найдите количество точек,
в которых касательная к графику функции параллельна прямой у=6.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Наименьшее и наибольшее значение функции, 11 класс
Содержание
- 2. Найти значение выражения:
- 3. На рисунке изображен график
- 4. На рисунке изображен график
- 5. На рисунке изображен график
- 6. На рисунке изображен график
- 7. На рисунке изображен график
- 8. На рисунке изображен график
- 9. На рисунке изображен график
- 10. На рисунке изображен график
- 11. На рисунке изображен график
- 12. На рисунке изображен график
- 13. На рисунке изображен график
- 14. Тема урока:Наибольшее и наименьшее значение функции.
- 15. ° НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО
- 16. Найти наибольшее значение функции по её графику
- 17. Найти наименьшее значение функции по её графику
- 18. ababПредположим, что функция f не имеет на
- 19. ababПусть теперь функция f имеет на отрезке
- 20. ababПредположим, что функция f имеет на отрезке
- 21. Если непрерывная на промежутке функция имеет единственную
- 22. Найти производную функции f'(x);Найти точки экстремума f'(x)=0;Выбрать
- 23. Найдите наименьшее значение функции y = x3
- 24. Найдем критические точки, которые принадлежат заданному отрезку.Выбрать
- 25. Найдем критические точки, которые принадлежат заданному отрезку.Выбрать
- 27. Скачать презентацию
- 28. Похожие презентации
Найти значение выражения:
![ababПредположим, что функция f не имеет на отрезке [а; b] критических точек.](/img/tmb/7/670255/08ba6a0a5a5b481e90e4eb87ffe9a65e-720x.jpg "Презентация по алгебре на тему Наименьшее и наибольшее значение функции, 11 класс")
![ababПусть теперь функция f имеет на отрезке [а; b] конечное число критических](/img/tmb/7/670255/19f549ac8d8375ee88436cc8be0c6a5c-720x.jpg "Презентация по алгебре на тему Наименьшее и наибольшее значение функции, 11 класс")
![ababПредположим, что функция f имеет на отрезке [а; b] одну точку экстремума.Если](/img/tmb/7/670255/bdf65da44980734674aed18310275f65-720x.jpg "Презентация по алгебре на тему Наименьшее и наибольшее значение функции, 11 класс")
Слайд 4 На рисунке изображен график производной
функции f '(x), определенной на интервале (–5;5) Найдите количество
точек, в которых касательная к графику функции параллельна прямой у = –2х+2 или совпадает с ней.
Слайд 5 На рисунке изображен график функции
f (x), определенной на интервале (–4;9) Определите количество целых
точек, в которых производная функции отрицательна.
Слайд 6 На рисунке изображен график функции
f (x), определенной на интервале (–3;9) Найдите количество точек,
в которых касательная к графику функции параллельна прямой у=-7.
Слайд 7 На рисунке изображен график производной
функции f '(x), определенной на интервале (–2;9) В какой
точке отрезка [2;6] f (x) принимает наибольшее значение..+
Слайд 8 На рисунке изображен график производной
функции f '(x), определенной на интервале (–5;7) . Найдите
промежутки возрастания функции f (x) . В ответе укажите сумму целых точек, входящих в эти промежутки.
Слайд 9 На рисунке изображен график производной
функции f '(x), определенной на интервале (–2;12) Найдите промежутки
убывания функции f (x) . В ответе укажите сумму целых точек, входящих в эти промежутки.
Слайд 10 На рисунке изображен график производной
функции f '(x), определенной на интервале (–11;3) Найдите промежутки
убывания функции f(x) . В ответе укажите длину наибольшего из них.
Слайд 11 На рисунке изображен график производной
функции f '(x), определенной на интервале (–5;6) Найдите точку
экстремума функции на отрезке[–4;4] .
Слайд 12 На рисунке изображен график функции
f (x) и касательная к нему в точке с
абсциссой х0 . Найдите значение производной функции в точке х0 .
Слайд 13 На рисунке изображен график функции
f (x) и касательная к нему в точке с
абсциссой х0 . Найдите значение производной функции в точке х0 .
Слайд 15 ° НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
ПО ГРАФИКУ. ° АЛГОРИТМ НАХОЖДЕНИЯ НАИБОЛЬШЕГО И
НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ ПО СХЕМЕ. ° РЕШАТЬ ЗАДАЧИ НА ОТЫСКАНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ.Цели урока:
Слайд 16 Найти наибольшее значение функции по её графику на
отрезках [ - 2; 6] и [ 0; 4]
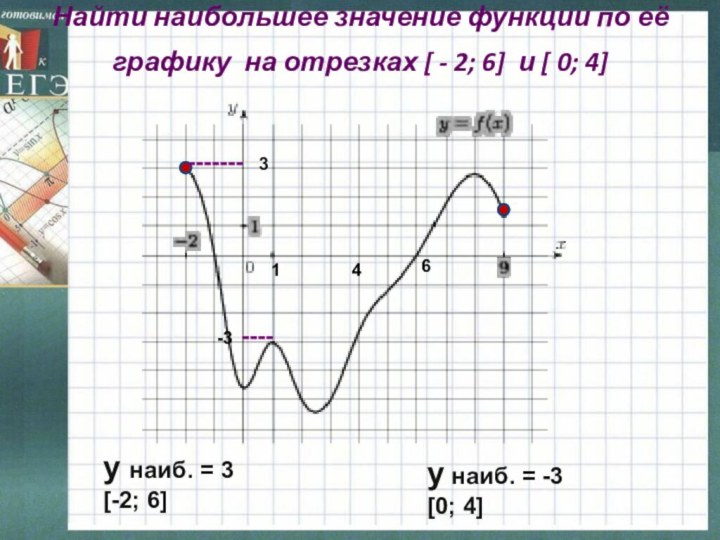
у наиб. = 3
[-2; 6]
4
-------
3
6
у наиб. = -3
[0; 4]
-3
----
1
Слайд 17 Найти наименьшее значение функции по её графику на
отрезках [ - 8; 0] и [ -2; 3]
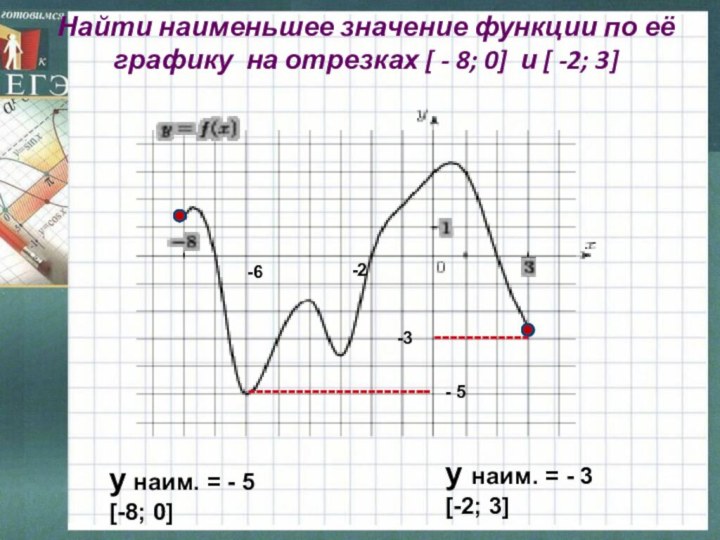
у наим. = - 5
[-8; 0]
у наим. = - 3
[-2; 3]
-2
-6
- 5
------------
-3
-----------------------
Слайд 18
a
b
a
b
Предположим, что функция f
не имеет на отрезке
[а; b] критических точек.
Тогда она возрастает (рис. 1)
или убывает (рис. 2) на этом отрезке.Значит,
наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b.
функция возрастает
функция убывает
Слайд 19
a
b
a
b
Пусть теперь функция f имеет на отрезке [а;
b] конечное число критических точек.
Наибольшее и наименьшее значения
функция f может принимать в критических точках функции или в точках а и b. Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Примеры
Слайд 20
a
b
a
b
Предположим, что функция f
имеет на отрезке [а;
b] одну точку экстремума.
Если это точка минимума, то в
этой точке функция будет принимать наименьшее значение. Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.
Слайд 21 Если непрерывная на промежутке функция имеет единственную точку
экстремума х0, то в случае максимума – значение f(х0)
наибольшее на этом промежутке, а в случае минимума – значение f(х0) наименьшее на этом промежутке.
Слайд 22
Найти производную функции f'(x);
Найти точки экстремума f'(x)=0;
Выбрать из
них точки
Вычислить значения функции в точках
Выбрать среди
них наибольшее и наименьшее. Записать ответ: Наибольшее f(x)=…
Наименьшее f(x)=…
Алгоритм
Слайд 23 Найдите наименьшее значение функции y = x3 –
27x на отрезке [0; 4]
1.
Найдем критические точки, которые принадлежат
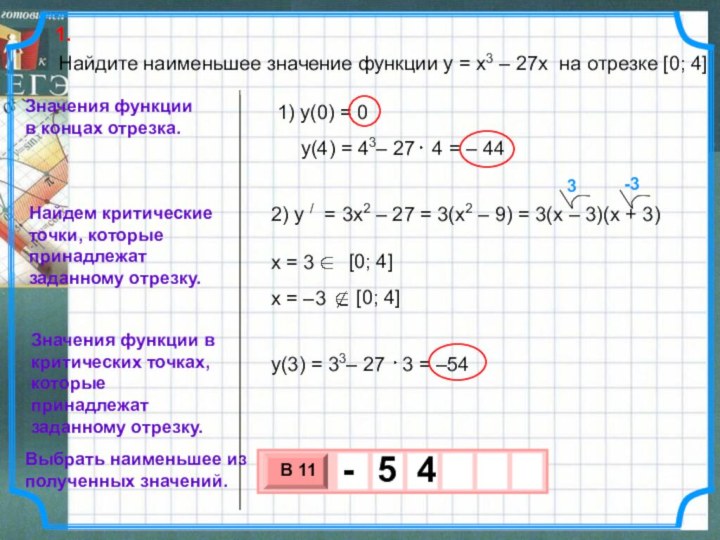
заданному отрезку.Выбрать наименьшее из полученных значений.
1) y(0) = 0
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 24
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее
из полученных значений.
1) y(0) = 4
2) y
/ = 3x2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
2.
Слайд 25
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее
из полученных значений.
1) y(1) = 1 – 2
+ 1 + 3 = 3 y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3x2 – 4x + 1=
y(1) = 3
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наименьшее значение функции y = x3 – 2x2 + x +3
на отрезке [ 1; 4 ]
3.
3x2 – 4x + 1 = 0
D=16–4*3*1=4
Слайд 26
Учебник Алимова Ш.А.: §30, №573, 574, 575(чётные), 576
Домашнее
задание:п.52, № 938 (2), 944(2,3)
Работа в классе:
№ 936,937, 938 (1,3),
944(1), 939 (1), 940.
