конкретных значений
Если x = 0, то
Если x =1,
то Если x = 4, то
Если x = 6,25, то
Если x = 9, то
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
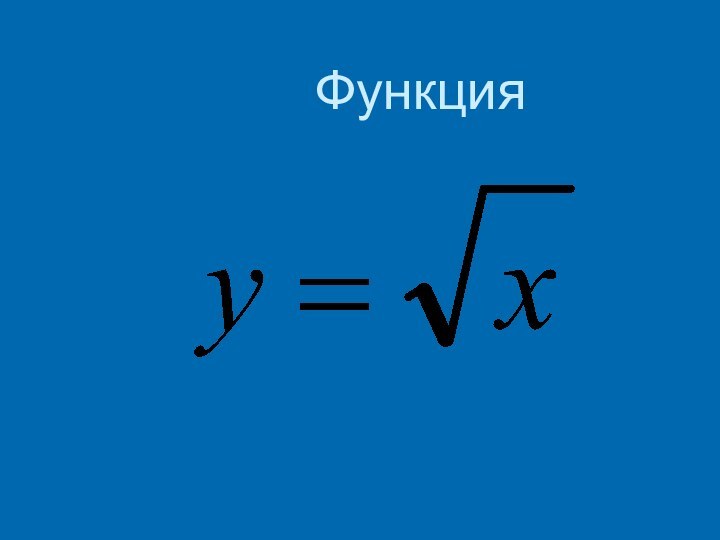


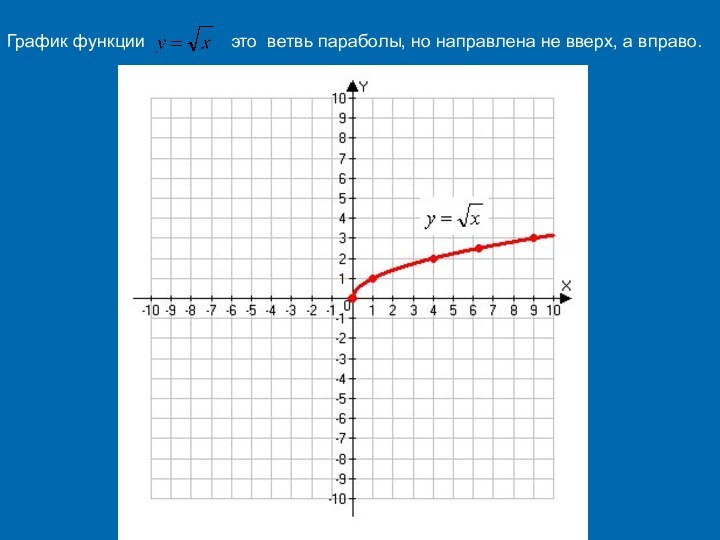

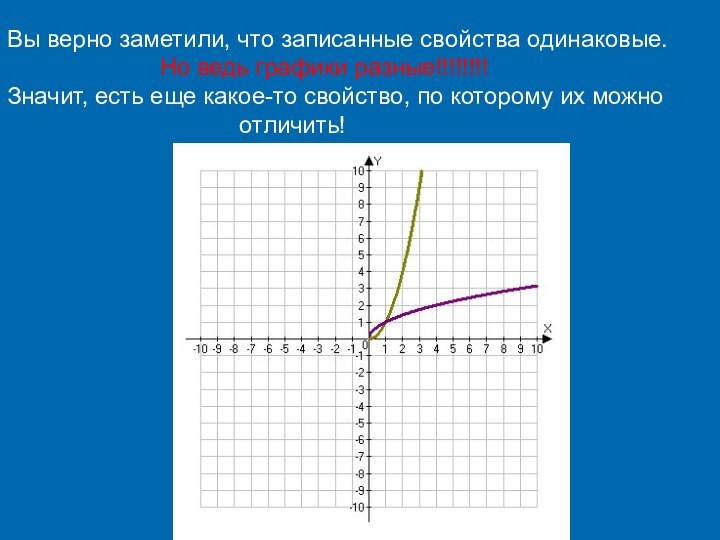
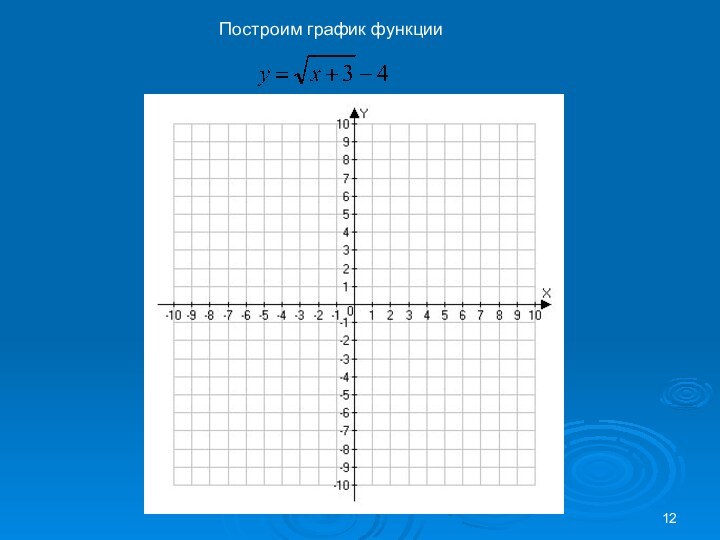
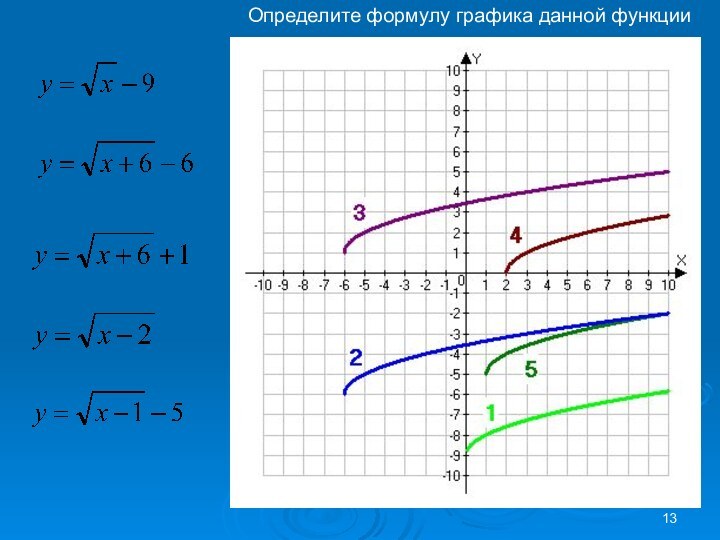

Если x = 4, то
Если x = 6,25, то
Если x = 9, то
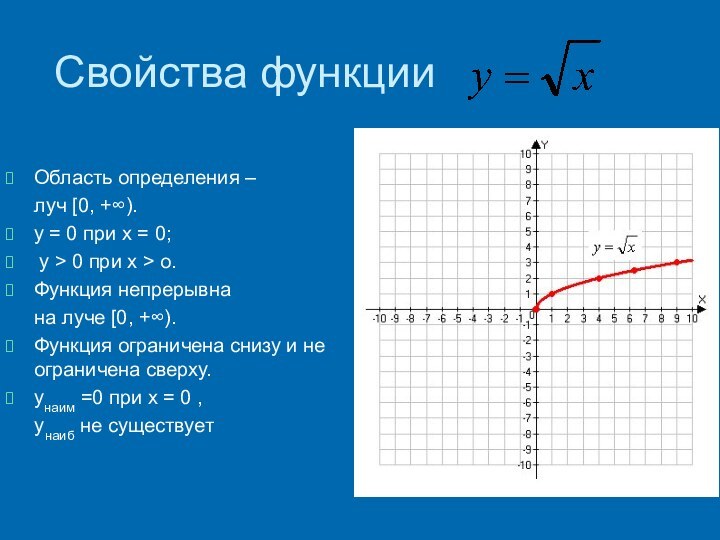
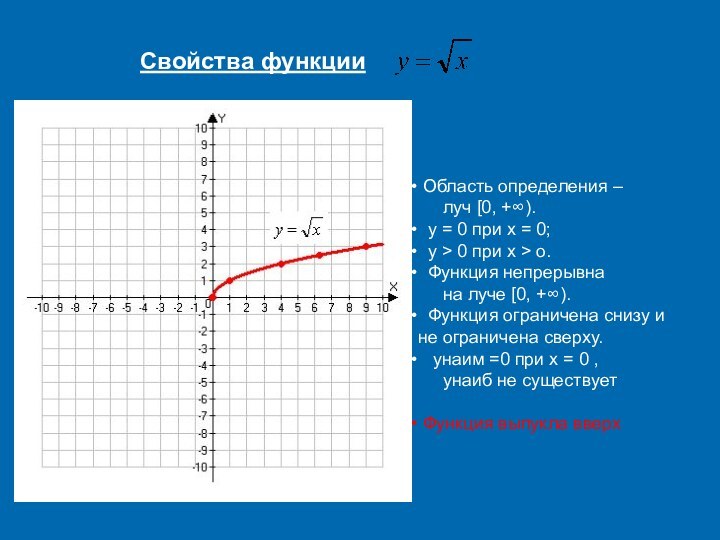
Область определения –
луч [0, +∞).
y = 0 при x = 0;
y > 0 при x > o.
Функция непрерывна на
луче [0, +∞).
Функция ограничена снизу и не ограничена сверху.
yнаим =0 при x = 0 ,
yнаиб не существует.
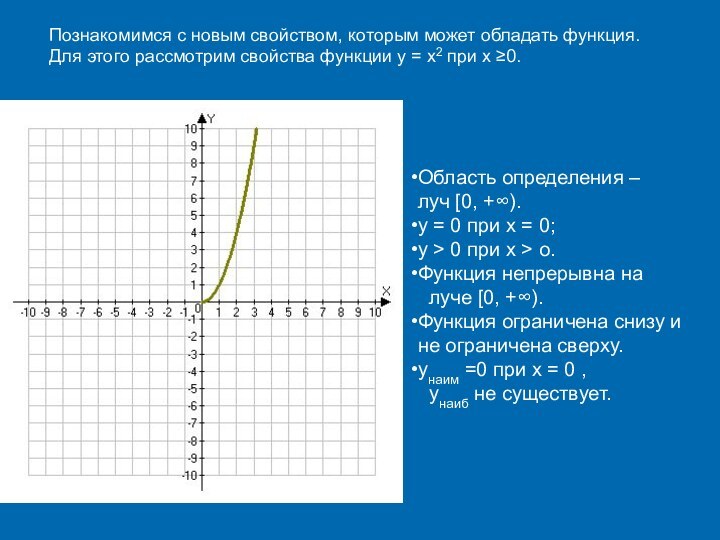
Свойства функции
y = x2 при x ≥0.
Область определения –
луч [0, +∞).
y = 0 при x = 0;
y > 0 при x > o.
Функция непрерывна
на луче [0, +∞).
Функция ограничена снизу и не ограничена сверху.
yнаим =0 при x = 0 ,
yнаиб не существует
Свойства функции