в нашей жизни встречаются логарифмы и нужны ли они?
3)
Узнать, что такое логарифмическая спираль в жизни?4) Роль логарифмов в природе, музыке, химии.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к проекту Логарифмы
Содержание
- 2. Цели проекта:1) Узнать историю происхождения логарифмов.2) Понять,
- 3. Что такое логарифм ?Логари́фм числа b по
- 4. Из определения следует, что нахождение:равносильно решению уравнения:
- 5. Пример:Например,
- 6. Вычисление логарифма называется логарифмированием. Числа a,b чаще
- 7. Кто создал?Определение логарифмов и таблицу их значений
- 8. Создатель.
- 9. История логарифмов.Непер хотел заменить
- 10. Книга Непера.В 1614 году Непер опубликовал в
- 11. Функция Непера.Строго говоря, Непер табулировал не ту
- 13. Современные представления.Современное определение логарифмирования — как
- 14. Вещественный логарифм.
- 15. Вещественный логарифмЛогарифм вещественного числапо определению есть решение уравненияВещественный логарифм имеет смысл при
- 16. Свойства вещественного логарифма.1 Основное логарифмическое тождество.2 Логарифмы
- 17. Комплексный логарифм.
- 18. Комплексный логарифм. Для комплексных чисел логарифм определяется
- 19. Комплексный логарифм существует для любогои его вещественная
- 20. Полезность.Логарифмические таблицы, расширенные и уточнённые другими математиками,
- 21. Логарифмическая спираль.
- 22. Логарифми́ческая спира́ль или изогональная спираль — особый
- 23. Создатель.Логарифмическая спираль была впервые описана Декартом и
- 24. Логарифмы в природе.Известно, что живые существа обычно
- 25. Рога таких млекопитающих, как архары (горные козлы),
- 26. По логарифмической спирали формируется и тело циклона.
- 27. Хищные птицы кружат над добычей по логарифмической
- 28. Актуальный pH крови - отрицательный логарифм концентрации
- 29. Логарифмы в космосе.Яркость звезд составляет геометрическую прогрессию
- 30. Логарифмы в музыке.Ступени темперированной хроматической гаммы (12-
- 31. Логарифмы в психологии.Ощущения, воспринимаемые органами чувств человека,
- 32. Изучение логарифмов.Эйлер принадлежит к числу гениев, чьё
- 33. Скачать презентацию
- 34. Похожие презентации
Цели проекта:1) Узнать историю происхождения логарифмов.2) Понять, где в нашей жизни встречаются логарифмы и нужны ли они?3) Узнать, что такое логарифмическая спираль в жизни?4) Роль логарифмов в природе, музыке, химии.
Слайд 2
Цели проекта:
1) Узнать историю происхождения логарифмов.
2) Понять, где
в нашей жизни встречаются логарифмы и нужны ли они?
Узнать, что такое логарифмическая спираль в жизни?4) Роль логарифмов в природе, музыке, химии.
Слайд 3
Что такое логарифм ?
Логари́фм числа b по основанию
a (от греч.) определяется как показатель степени, в которую
надо возвести основание a, чтобы получить число b.Обозначение:
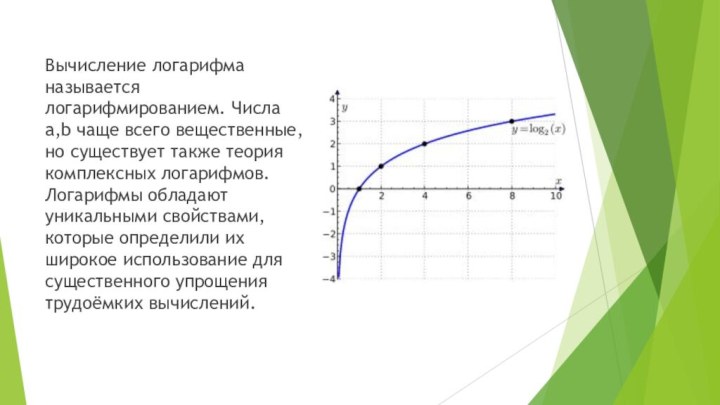
Слайд 6 Вычисление логарифма называется логарифмированием. Числа a,b чаще всего
вещественные, но существует также теория комплексных логарифмов. Логарифмы обладают
уникальными свойствами, которые определили их широкое использование для существенного упрощения трудоёмких вычислений.
Слайд 7
Кто создал?
Определение логарифмов и таблицу их значений (для
тригонометрических функций) впервые опубликовал в 1614 году шотландский математик
Джон Непер (1550—1617) — шотландский математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц.
8-й представитель нетитулованного дворянства в Шотландии.
Слайд 9
История логарифмов.
Непер хотел заменить трудоёмкое
умножение на простое сложение, сопоставив с помощью специальных таблиц
геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.
Слайд 10
Книга Непера.
В 1614 году Непер опубликовал в Эдинбурге
сочинение под названием «Описание удивительной таблицы логарифмов» . Там
было краткое описание логарифмов и их свойств, а также семизначные таблицы логарифмов синусов, косинусов и тангенсов .
Слайд 11
Функция Непера.
Строго говоря, Непер табулировал не ту функцию,
которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x),
то она связана с натуральным логарифмом (ln) следующим образом.Слайд 12
Историческая справка.
Через десяток лет после появления логарифмов английский
ученый Гунтер изобрел очень популярный прежде счетный прибор –логарифмическую линейку. Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ достаточной точностью в три значащие цифры. Теперь ее вытеснили калькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни микрокалькуляторы.
Слайд 13
Современные представления.
Современное определение логарифмирования — как операции,
обратной возведению в степень — впервые появилось у Валлиса
и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область
Слайд 15
Вещественный логарифм
Логарифм вещественного числа
по определению есть решение уравнения
Вещественный
логарифм
имеет смысл при
Слайд 16
Свойства вещественного логарифма.
1 Основное логарифмическое тождество.
2 Логарифмы единицы
и числа, равного основанию.
3 Логарифм произведения, частного от деления,
степени и корня.4 Замена основания логарифма.
5 Неравенства.
Слайд 18
Комплексный логарифм.
Для комплексных чисел логарифм определяется так же,
как вещественный. На практике используется почти исключительно натуральный комплексный
логарифм, который обозначаетсяи определяется как решение
И является многозначной.
Слайд 19
Комплексный логарифм существует для любого
и его вещественная часть
определяется однозначно, в то время как мнимая часть имеет
бесконечное множество значений, различающихся на целое кратное
Слайд 20
Полезность.
Логарифмические таблицы, расширенные и уточнённые другими математиками, повсеместно
использовались для научных и инженерных расчётов более трёх веков,
пока не появились электронные калькуляторы и компьютеры.Слайд 22 Логарифми́ческая спира́ль или изогональная спираль — особый вид
спирали, часто встречающийся в природе. Является траекторией точки ,
которая движется вдоль равномерно вращающейся прямой.
Слайд 23
Создатель.
Логарифмическая спираль была впервые описана Декартом и позже
интенсивно исследована Якобом Бернулли, который называл её Spiramirabilis —
«удивительная спираль».
Слайд 24
Логарифмы в природе.
Известно, что живые существа обычно растут,
сохраняя общее начертание своей формы. Некоторым моллюскам чтобы не
слишком вытягиваться в длину, приходится скручиваться .Слайд 25 Рога таких млекопитающих, как архары (горные козлы), закручены
по логарифмической спирали.
По логарифмическим спиралям закручены многие галактики, в
частности Галактика, которой принадлежит солнечная система.
Слайд 26
По логарифмической спирали формируется и тело циклона.
Один
из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити
вокруг центра по логарифмической спирали.Слайд 27 Хищные птицы кружат над добычей по логарифмической спирали.
Так им удобнее смотреть на добычу.
По логарифмическим спиралям выстраиваются
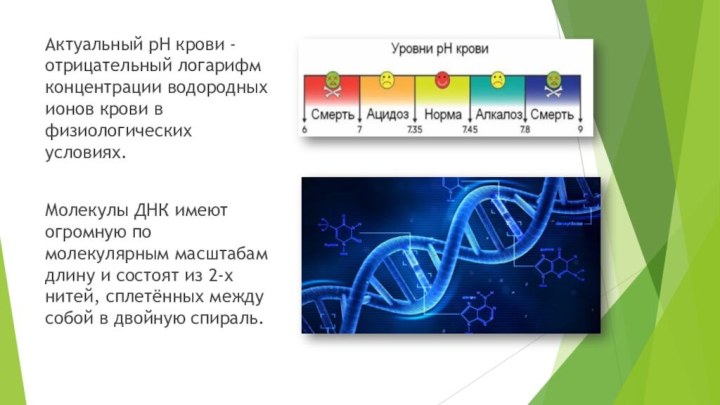
цветки в соцветиях подсолнечника.Слайд 28 Актуальный pH крови - отрицательный логарифм концентрации водородных
ионов крови в физиологических условиях.
Молекулы ДНК имеют огромную по
молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль.
Слайд 29
Логарифмы в космосе.
Яркость звезд составляет геометрическую прогрессию со
знаменателем 2,5 . Оценивая яркость звезд, астроном пользуется таблицей
логарифмов.Аналогично оценивается и громкость шума.
Слайд 30
Логарифмы в музыке.
Ступени темперированной хроматической гаммы (12- звуковой
) частот звуковых колебаний представляют собой логарифмы .
Основание
этих логарифмов равно 2.
Слайд 31
Логарифмы в психологии.
Ощущения, воспринимаемые органами чувств человека, могут
вызываться раздражениями, отличающимися друг от друга во много раз.
Опыты показали, что организм как бы «логарифмирует» полученные им раздражения. Вредное влияние промышленных шумов на здоровье рабочих побудило выработать приёмы точной числовой оценки громкости шума.
Слайд 32
Изучение логарифмов.
Эйлер принадлежит к числу гениев, чьё творчество
стало достоянием всего человечества. До сих пор школьники всех
стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер.Студенты проходят высшую математику по руководствам, первыми образцами которых явились классические монографии Эйлера.
