- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Численные методы решения уравнений
Содержание
- 2. методы Метод касательныхМетод половинногоМетод половинного деленияМетод хордМетод комбинированныйМетод итераций
- 3. Пусть корень ξ уравнения f (x) отделён
- 4. xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a;
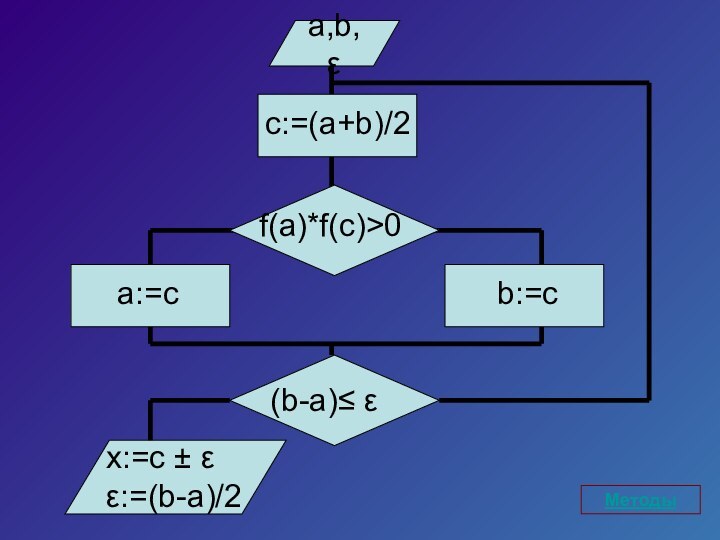
- 5. a,b, εf(a)*f(c)>0a:=cx:=c ± εε:=(b-a)/2c:=(a+b)/2b:=c(b-a)≤ εМетоды
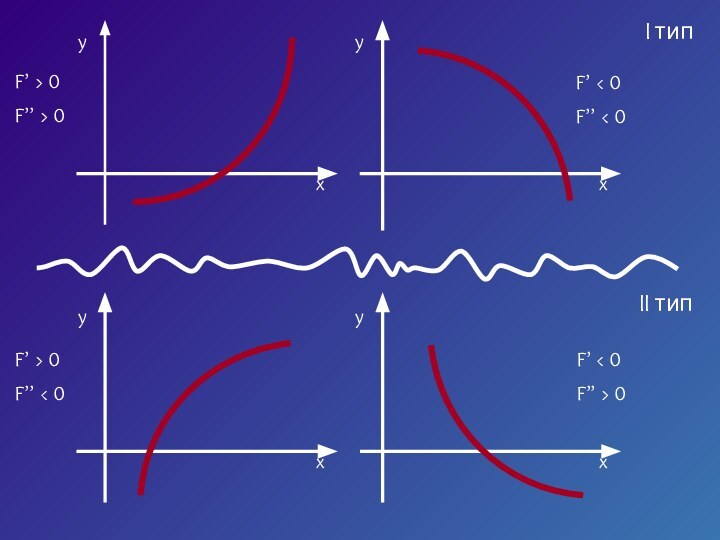
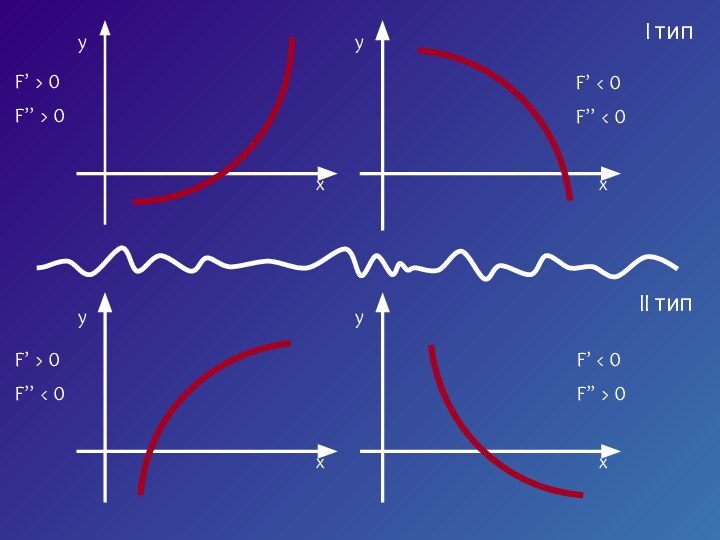
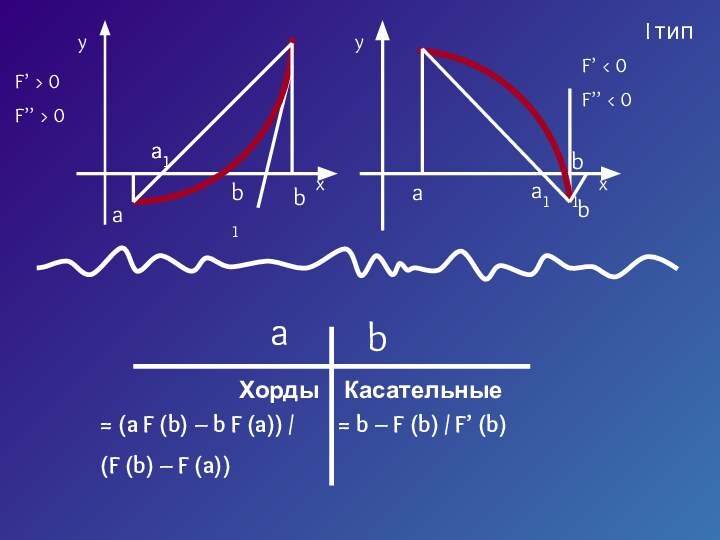
- 6. I типII тип
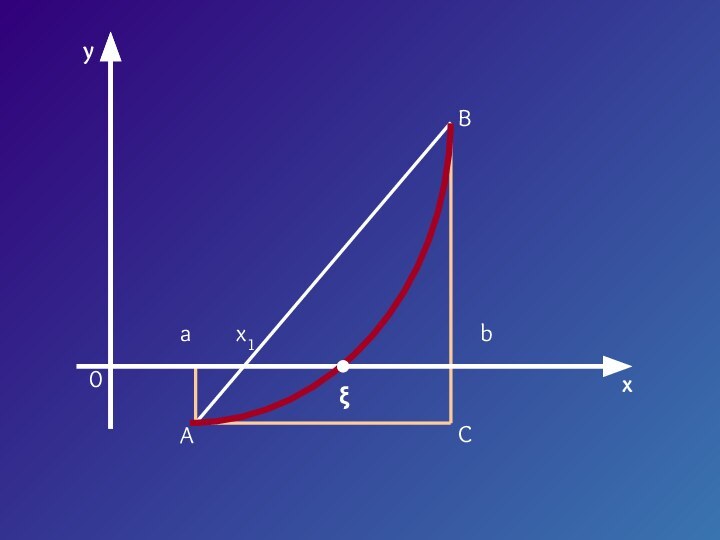
- 7. Пусть корень уравнения F (x) = 0
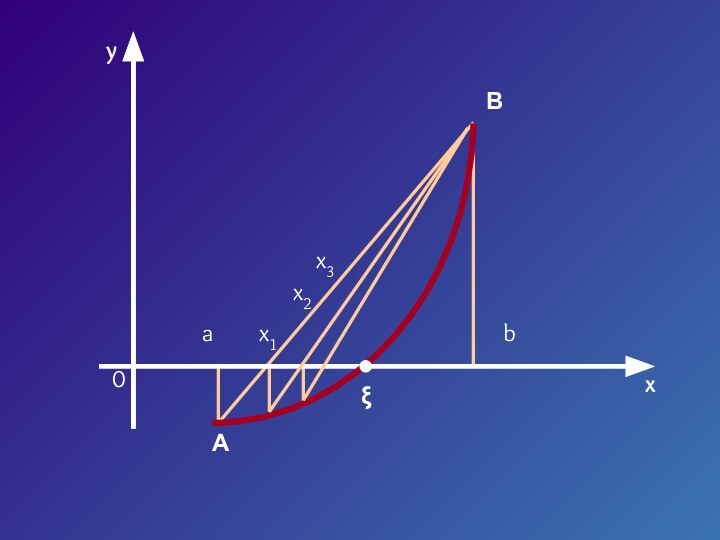
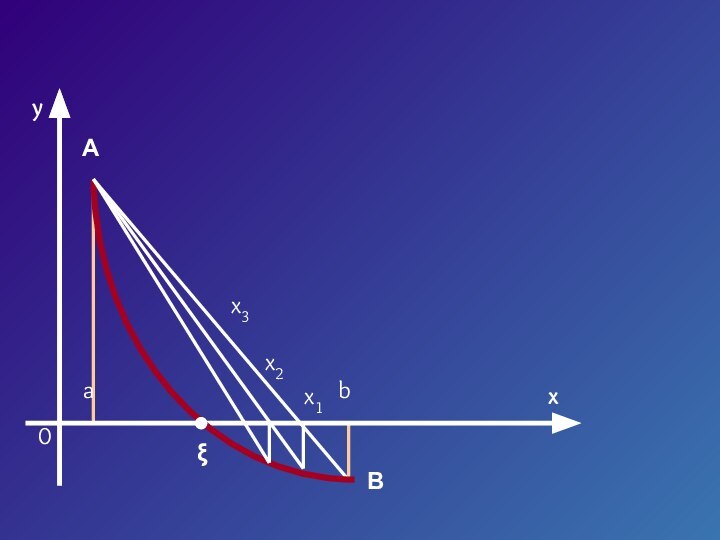
- 8. yx0abx1x2x3ξAB
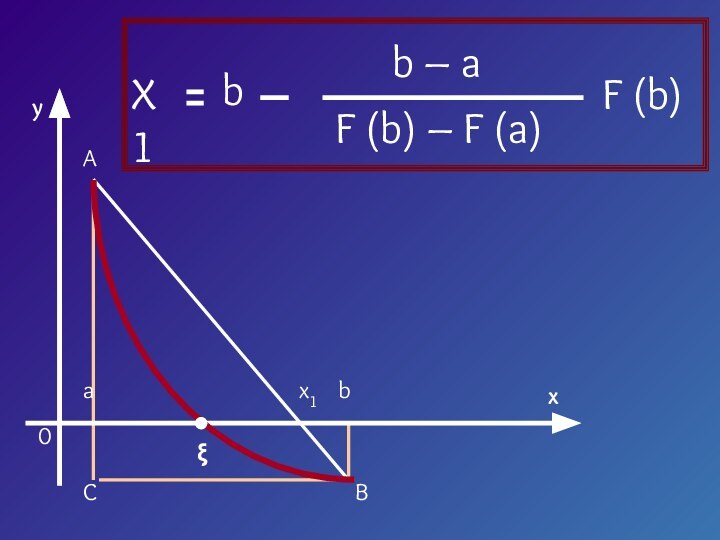
- 9. yx0abx1ξACB
- 10. Треугольник AaX1 подобен треугольнику ABCX1 – a
- 12. yx0abx2ξx1x3AB
- 13. yx0abx1ξACB
- 14. Методы
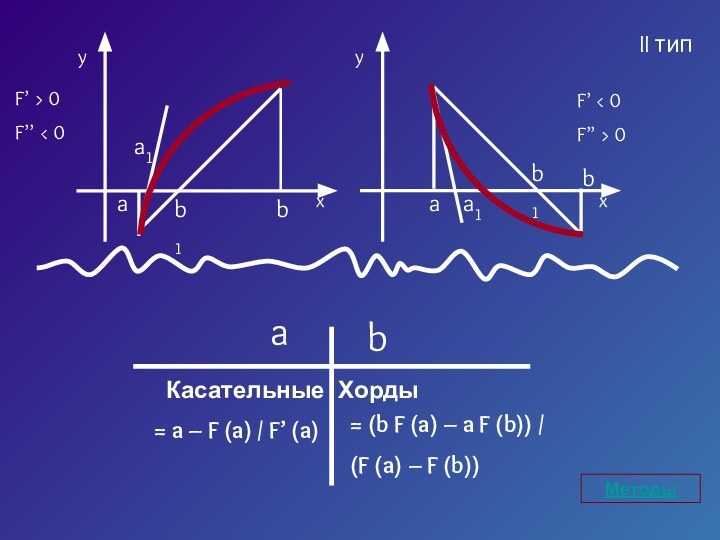
- 15. I типII тип
- 16. Пусть корень ξ уравнения F (x) =
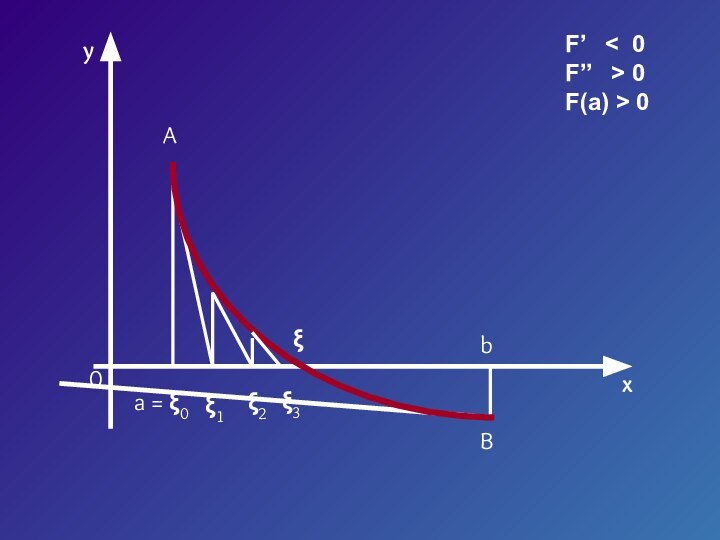
- 17. yx0a = ξ0 bξ1 ξ2 ABF’ < 0F’’ > 0F(a) > 0ξ ξ3
- 18. Уравнение касательной в точке A (a, F
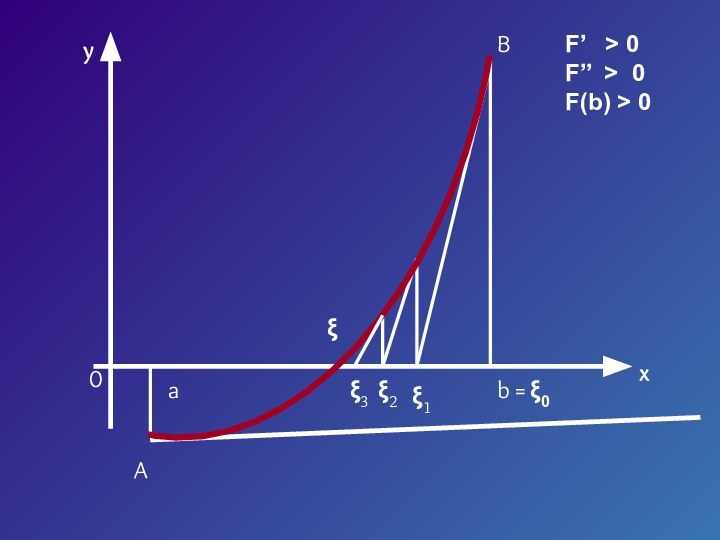
- 19. yx0ab = ξ0ξ1 ξ2 ABF’ > 0F’’ > 0F(b) > 0ξ ξ3
- 20. Если касательную к кривой провести в точке B (в правом конце), то получим
- 21. Методыx0 = a II типx0 = b I тип
- 22. I типХордыbaКасательные= (a F (b) – b
- 23. II типХордыbaКасательные= (b F (a) – a
- 26. Скачать презентацию
- 27. Похожие презентации
методы Метод касательныхМетод половинногоМетод половинного деленияМетод хордМетод комбинированныйМетод итераций


![Численные методы решения уравнений Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём](/img/tmb/11/1045673/900eb5aac744ca44ae65f1f9efb3af86-720x.jpg)
![Численные методы решения уравнений xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a; c] и [c; b], длина](/img/tmb/11/1045673/fd85a5ef7e2ddfc9a319a2de91cc05aa-720x.jpg)
![Численные методы решения уравнений Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b].Будем](/img/tmb/11/1045673/caff13610115c60200de27c819ff46c3-720x.jpg)

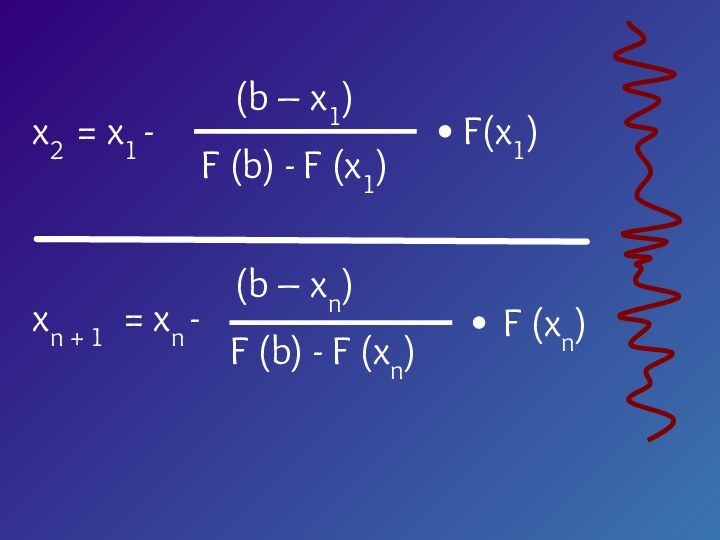




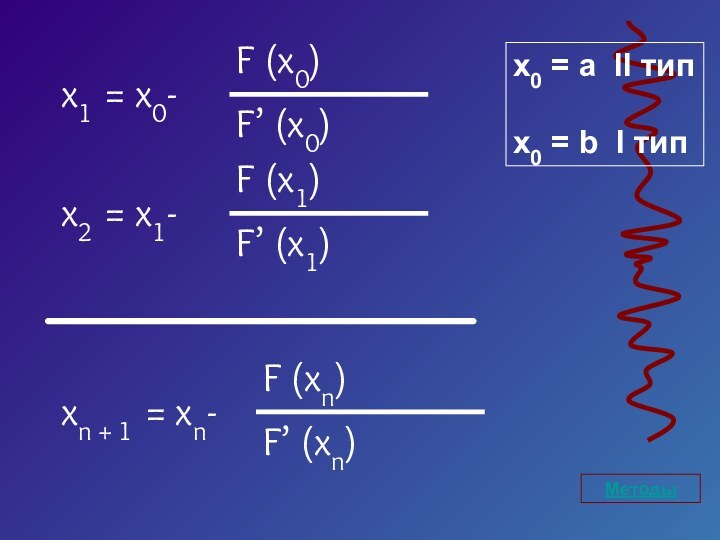



Слайд 2
методы
Метод касательных
Метод половинногоМетод половинного деления
Метод хорд
Метод комбинированный
Метод
итераций
Слайд 3 Пусть корень ξ уравнения f (x) отделён на
отрезке [a, b], причём b – a > ε
Будем
считать, что функция:1)Непрерывна и монотонна на отрезке [a, b]
2)f (a) x f (b) < 0
Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2
Отрезок [a, b] разделен на два отрезка [a, c] и [c, b], длина каждого = (b – a) / 2
Слайд 4
x
y
a
b
c
C = (a + b) / 2
a1
b1
c1
a2
b2
c2
b-a>ε
[a; c]
и [c; b], длина отрезков (b - a) /
2[an; bn ], длина (b-a)/2n
(b-a)/2n <=ε
Приближенное значение корня
Cn = (an + bn) / 2 с погрешностью,
не превышающей (b-a)/2n+1
0
ξ
Слайд 7 Пусть корень уравнения F (x) = 0 отделен
на отрезке [a, b].
Будем считать:
F (x) непрерывна на отрезке
[a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.
F (a) * F (b) < 0
Слайд 16 Пусть корень ξ уравнения F (x) = 0
отделен на отрезке [a, b].
Будем считать:
F (x) непрерывна на
отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.
F (a) * F (b) < 0
Слайд 18 Уравнение касательной в точке A (a, F (a))
:
y – F (a) = F’ (a)*(x – a).
Полагая
y = 0, x = ξ 1 , получим