где n - заданное действительное число.
Частные случаи степенной функции
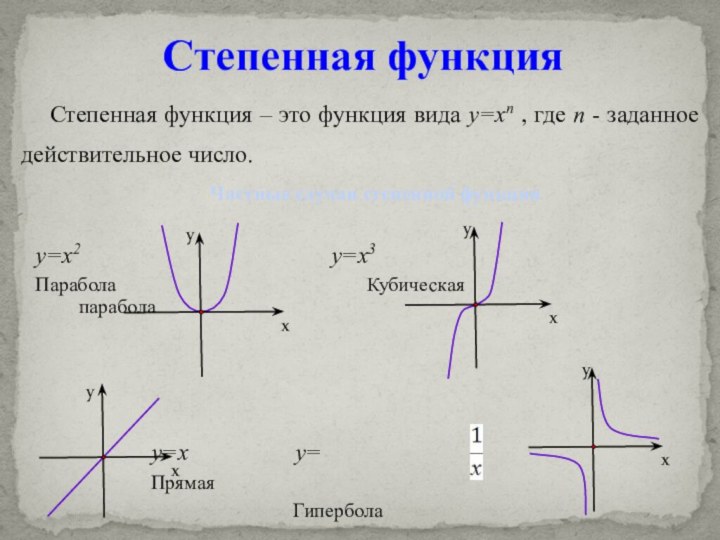
y=x2
y=x3Парабола Кубическая парабола
y=x y=
Прямая
Гипербола
Степенная функция
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

















Степенная функция
Степень с рациональным показателем
Степень с отрицательным
дробным показателем
Свойства степени
с рациональным показателем
Корень n-ой степени
Арифметический корень
n-ой степени
Свойства корня n-ой степени