Презентация на тему Числовая окружность на координатной плоскости. 10 класс

координаты числовой окружности.
Как искать координату числовой окружности?
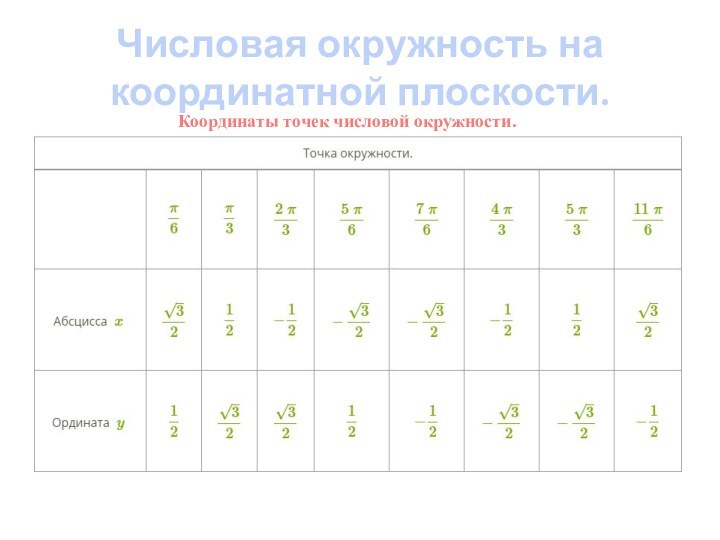
Таблица основных координат

числовой окружности.

Примеры задач.

координатной плоскости так, чтобы центр окружности совместился с началом

координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).

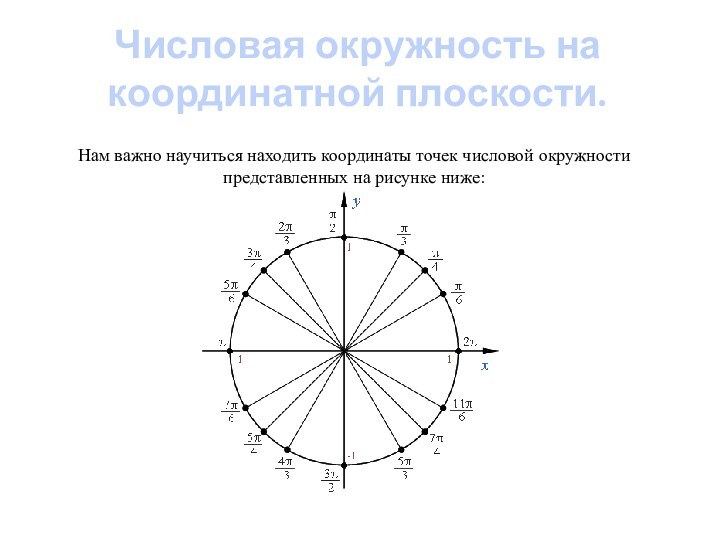
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
x > 0, у > 0 в первой четверти;
х < 0, у > 0 во второй четверти;
х < 0, у < 0 в третьей четверти;
х > 0, у < 0 в четвертой четверти.

Для любой точки М(х; у) числовой окружности выполняются неравенства -1 < x < 1; -1 < у < 1.

Запомните!

уравнение числовой окружности:

координаты точек числовой окружности представленных на рисунке ниже:

Точка М(π/4) — середина первой четверти. Опустим из точки

М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∡MOP=45° 
Значит, треугольник OMP - равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x = y
Так как координаты точки M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:

Решив данную систему получаем:

Получили, что координаты точки M, соответствующей числу π/4 будут

Аналогичным образом рассчитываются координаты точек представленных на предыдущем слайде.

и t+2π•k (k-целое число) соответствует одна и тоже точка

числовой окружности то:

45π/4 = (10 + 5/4) • π = 10π +5π/4 = 5π/4 + 2π•5

Значит, числу 45π/4 соответствует та же точка числовой окружности, что и числу 5π/4. Посмотрев значение точки 5π/4 в таблице получаем:

Числовая окружность на координатной плоскости.

и t+2π•k (k-целое число) соответствует одна и тоже точка

числовой окружности то:

-37π/3 = -(12 + 1/3) • π = -12π –π/3 = -π/3 + 2π•(-6)

Значит, числу -37π/3 соответствует та же точка числовой окружности, что и числу –π/3, а числу –π/3 соответствует та же точка что и 5π/3. Посмотрев значение точки 5π/3 в таблице получаем:

Числовая окружность на координатной плоскости.

= 1/2 и записать, каким числам t они соответствуют.

Пример
Прямая

у = 1/2 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π/6 (из данных таблицы) значит, и любому числу вида π/6 +2π •k . Точка Р соответствует числу 5π/6, а значит, и любому числу вида 5π/6 +2 π •k

Получили, как часто говорят в таких случаях, две серии значений: π/6 +2 π •k и 5π/6 +2 π •k

Ответ : t= π/6 +2 π •k и t= 5π/6 +2 π •k

Числовая окружность на координатной плоскости.

и записать, каким числам t они соответствуют.

Прямая

x = 1/2 пересекает числовую окружность в точках М и Р. Неравенству x ≥ соответствуют точки дуги РМ.
Точка М соответствует числу 3π/4 (из данных таблицы) значит, и любому числу вида -3π/4 +2π•k . Точка Р соответствует числу -3π/4, а значит, и любому числу вида –
-3π/4 +2 π •k

Тогда получим -3π/4 +2 π •k ≤t≤3π/4 +2 π •k
Ответ : -3π/4 +2 π •k ≤t≤3π/4 +2 π •k

Числовая окружность на координатной плоскости.