- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Логарифмы
Содержание
- 2. Исторический очеркXVI в. резко возрос объем работы
- 3. Первые таблицы логарифмов составлены независимо
- 4. Первые таблицы десятичных логарифмов (1617 г.) были
- 5. Непер Джон(1550—1617) —английский математик. Изобретатель логарифмов, составитель первой таблицы логарифмов,палочек Непера.
- 6. Логарифм -определяется как показатель степени, в
- 7. Вещественный логарифм Логарифм вещественного числа logab имеет смысл при Логарифм:Комплексный логарифм
- 8. Наиболее широкое применение нашли следующие виды логарифмов:
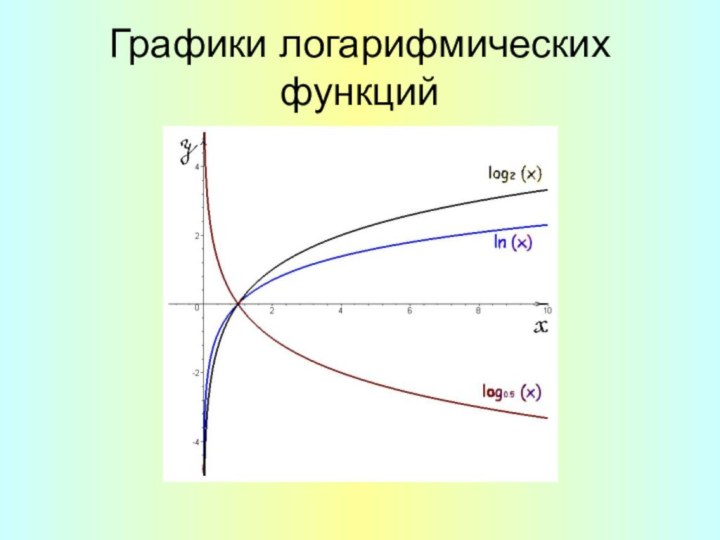
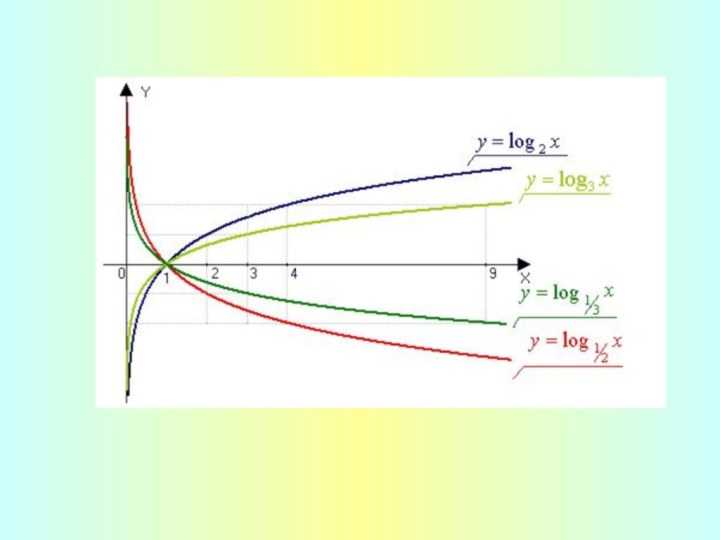
- 9. Графики логарифмических функций
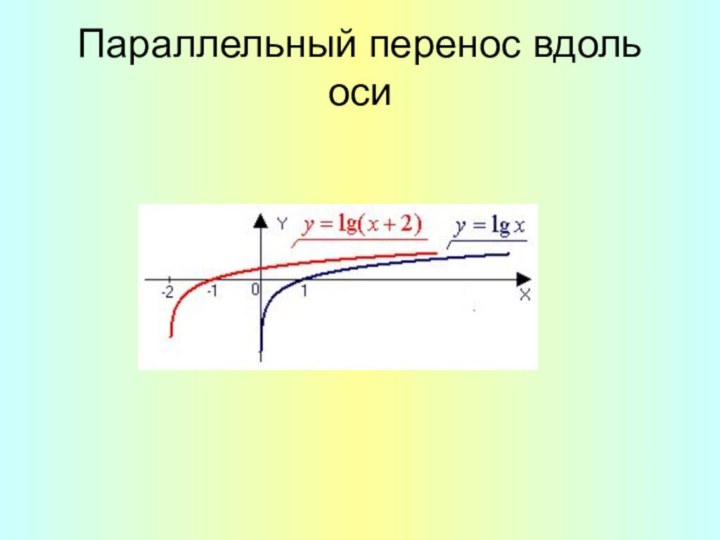
- 10. Параллельный перенос вдоль оси
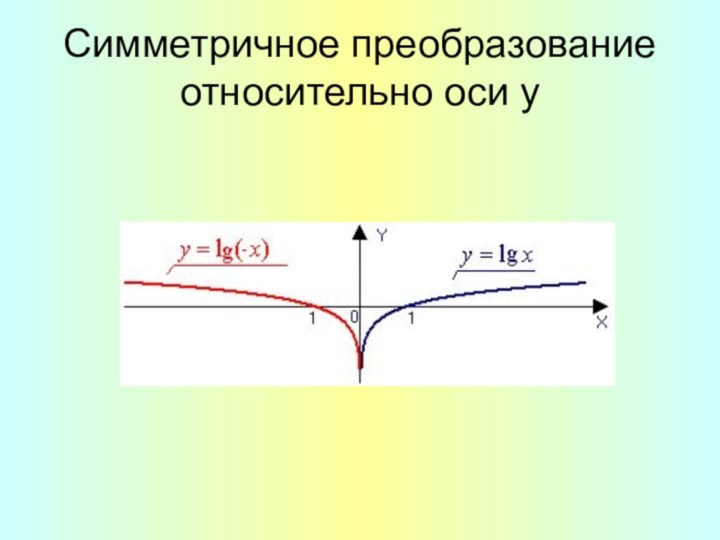
- 11. Симметричное преобразование относительно оси у
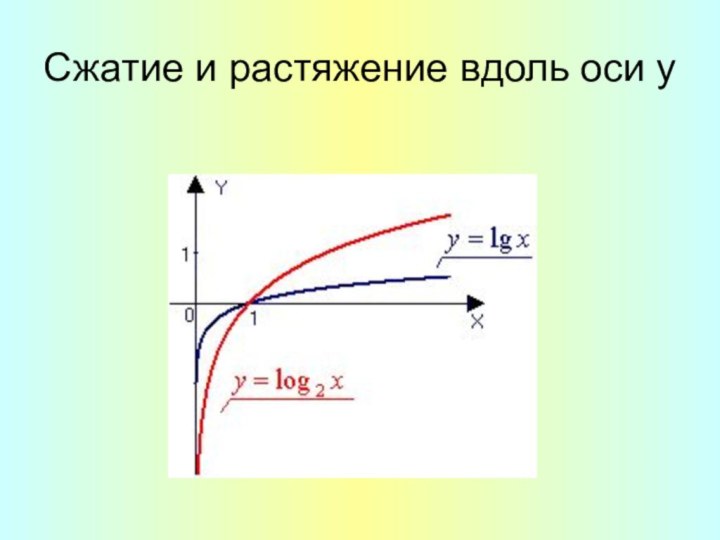
- 12. Сжатие и растяжение вдоль оси y
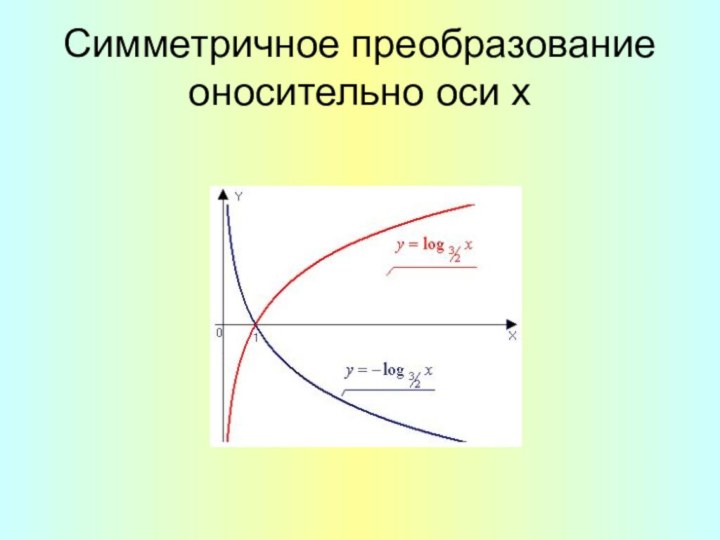
- 13. Симметричное преобразование оносительно оси х
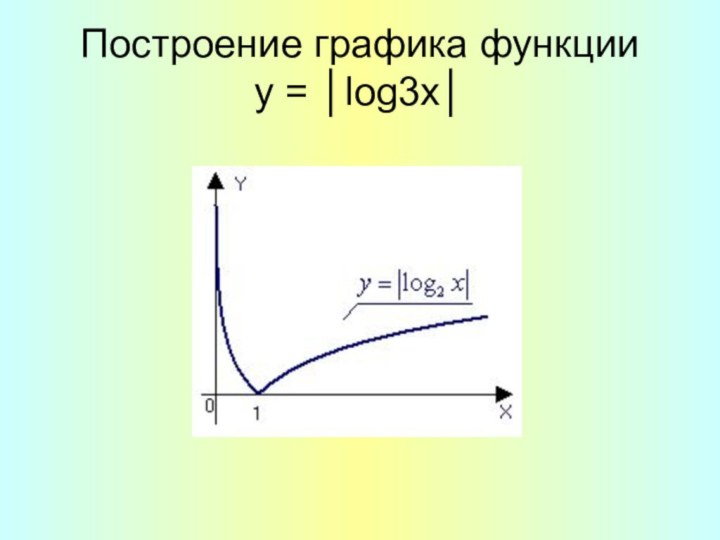
- 14. Построение графика функции y = │log3х│
- 16. Формула натурального логорифма:
- 17. Десятичные логарифмыЛогарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений.
- 18. Логарифмическая функция Функция вида f(x) =
- 19. Риманова поверхность Комплексная логарифмическая функция — пример
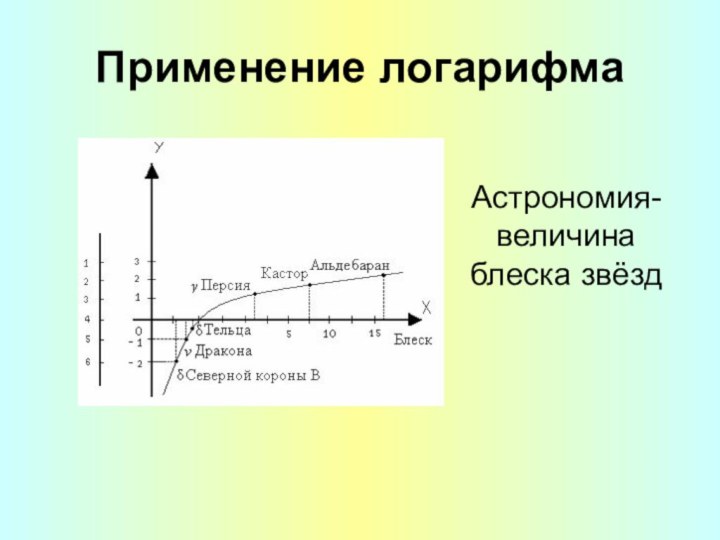
- 20. Применение логарифма Астрономия-величина блеска звёзд
- 21. Логарифмическая спираль Форму логарифмической спирали имеют не
- 22. Выводы: Логарифмической функцией называется функция вида f(x) = logax, определённая при
- 23. Свойства функции:Область определения (0; )Область
- 24. Применение логарифмической функцииЛогарифмическая функция крайне важна в
- 25. Скачать презентацию
- 26. Похожие презентации
Исторический очеркXVI в. резко возрос объем работы ,связанный с вычислениями. Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов необычайно быстро вошли в практику.








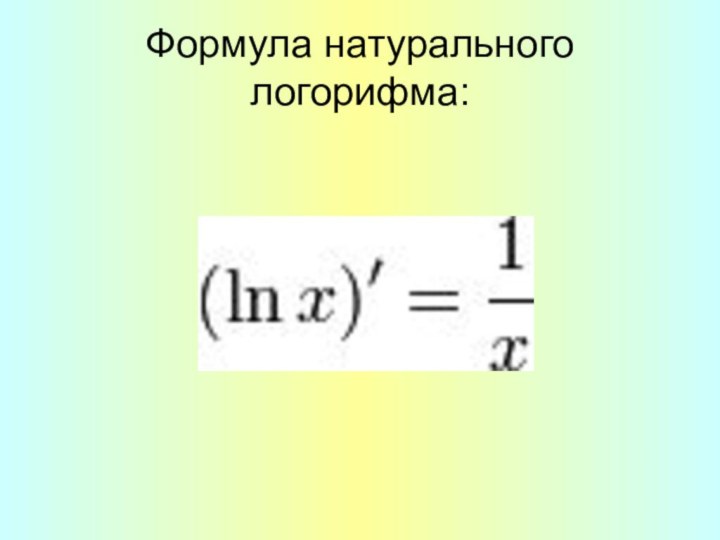







Слайд 3 Первые таблицы логарифмов составлены независимо друг
от друга шотландским математиком Дж. Непером (1550—1617) и швейцарцем
И. Бюрги (1552—1632).Непер Дж.
Слайд 4 Первые таблицы десятичных логарифмов (1617 г.) были составлены
по совету Непера английским математиком Г. Бриггсом (1561 —1630).
Многие из них были найдены с помощью выведенной Бриггсом приближенной формулыСлайд 5 Непер Джон(1550—1617) —английский математик. Изобретатель логарифмов, составитель первой
таблицы логарифмов,палочек Непера.
Слайд 6
Логарифм
-определяется как показатель степени, в которую
надо возвести основание a, чтобы получить число b.
Слайд 7 Вещественный логарифм Логарифм вещественного числа logab имеет смысл при
Логарифм:
Комплексный логарифм
Слайд 8
Наиболее широкое применение нашли следующие виды логарифмов:
Натуральные:
, основание: e (число Эйлера).
Десятичные:
, основание: число 10.Двоичные: или , основание: число 2.
Они применяются в теории информации и информатике.
Слайд 17
Десятичные логарифмы
Логарифмы по основанию 10 (обозначение: lg a)
до изобретения калькуляторов широко применялись для вычислений.
Слайд 18
Логарифмическая функция
Функция вида f(x) = logax,
определённая при
График любой логарифмической функции проходит через точку (1;0). Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.
Слайд 19
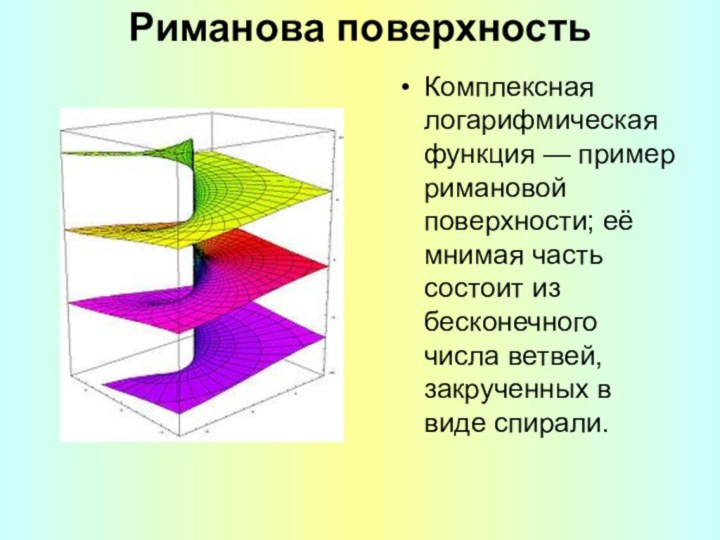
Риманова поверхность
Комплексная логарифмическая функция — пример римановой поверхности;
её мнимая часть состоит из бесконечного числа ветвей, закрученных
в виде спирали.
Слайд 21
Логарифмическая спираль
Форму логарифмической спирали имеют не только объекты
астрономии, но и например: ракушки многих улиток, рога козлов,
паутина паука , семечки подсолнуха.
Слайд 23
Свойства функции:
Область определения (0; )
Область значений
R
Чётность /нечётность: функция не является ни четной, ни нечетной
Нули
функции: y = 0 при x = 1Промежетки знакопостоянства: если 0 < a < 1, то y > 0 при x (0; 1), y < 0 при x (1; ) если a > 1, то y > 0 при x (1; ), y < 0 при x (0; 1)
Промежутки монотонности : при 0 < a < 1 функция убывает при x (0; ) при a > 1 функция возрастает при x (0; )
Экстренумов нет.
График функции проходит через точку: (1; 0)
Асимптота x = 0
Слайд 24
Применение логарифмической функции
Логарифмическая функция крайне важна в экономике,
физике, при проведении научных, экспериментальных расчетов, астрономии и др.
Форма логарифмической спирали присуща многим природным объектам.Физика — интенсивность звука (децибелы).
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.