решения задач, связанных с этой темой, базового и повышенного
уровня.Организовать работу учащихся соответственно уровню уже сформированных у них знаний.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Функция
Содержание
- 2. *Страница Цели урокаОбобщить теоретические знания по теме.
- 3. *Страница План урокаI этап – организационный
- 4. *Страница I этап - организационныйТема урока: «Определение,
- 5. *Страница II этап – повторение. Определение функции:Функцией
- 6. *Страница Является ли функцией?
- 7. *Страница Является ли функцией?
- 8. *Страница Является ли функцией?
- 9. *Страница Способы задания функцииОписательный: «Каждому двузначному числу поставлен в соответствие его квадрат»ТабличныйГрафическийАналитический
- 10. *Страница Общая схема исследования функцииОбласть определения функции
- 11. *Страница Область определения функции- Множество значений независимой
- 12. *Страница Найдите D(f)1. D(f)=(-∞; +∞)2. D(f)=(-∞; +∞)3. D(f)=(-∞; +∞)4. D(f)=(-∞; +∞)5. D(f)=(-∞; -4)U(-4;-2)U(-2; +∞)6. D(f)=(-∞; +∞)
- 13. *Страница Найдите D(f)7. D(f)=(-∞; 0)U(0; +∞)8. D(f)=(-∞;
- 14. *Страница Чётность функцииЕсли область определения функции симметрична
- 15. *Страница Исследуйте на чётность1. Ни чётная,
- 16. *Страница МонотонностьЕсли большему значению аргумента соответствует большее
- 17. *Страница Исследуйте на монотонность
- 18. *Страница Точки экстремума функцииЕсли в некоторой точке
- 19. *Страница Экстремумыy = f (x) 1 2
- 20. *Страница Периодичность функцииЕсли существует такое число t≠0,
- 21. *Страница Знакопостоянство функцииМножество Х, на котором функция не меняет свой знак, называется промежутком знакопостоянства функции
- 22. *Страница 1 2 3 4
- 23. *Страница Область значенийМножество, состоящее из всех значений, которые может принимать функция на своей области определения
- 24. *Страница Разминка
- 25. *Страница Функция у = f(x) задана графиком.
- 26. *Страница 243[0; 5]Функция у = f(x)
- 27. *Страница Функция у = f(x) определена графиком.
- 28. *Страница Функция у = f(x) задана
- 29. *Страница 1 2 3 4
- 30. *Страница 1 2 3 4
- 31. *Страница 1 2 3 4
- 32. *Страница 1 2 3 4
- 33. *Страница 1 2 3 4
- 34. *Страница Укажите график четной функции.4231ПОДУМАЙ!ПОДУМАЙ!Верно! График симметричен относительно оси ОуПОДУМАЙ!
- 35. *Страница Укажите график возрастающей функции.3421ПОДУМАЙ!Подумай!ПОДУМАЙ!Верно!
- 36. *Страница Укажите график функции, заданной формулой у = х – 2 – 2 3421ПОДУМАЙ!Подумай!ПОДУМАЙ!Верно!
- 37. *Страница Функция у =f (x), имеющая период
- 38. *Страница На рисунке изображен график производной функции
- 39. *Страница На рисунке изображен график производной функции
- 40. *Страница На рисунке изображен график производной функции
- 41. *Страница На рисунке изображен график производной функции
- 42. *Страница На рисунке изображен график производной функции
- 43. *Страница y = f /(x) 1342Не верно!Не верно!Не
- 44. *Страница y = f /(x)1 2
- 45. *Страница y = f /(x)1 2
- 46. *Страница III этап. Разноуровневая работа1 группа –
- 47. Скачать презентацию
- 48. Похожие презентации
*Страница Цели урокаОбобщить теоретические знания по теме. Рассмотреть решения задач, связанных с этой темой, базового и повышенного уровня.Организовать работу учащихся соответственно уровню уже сформированных у них знаний.
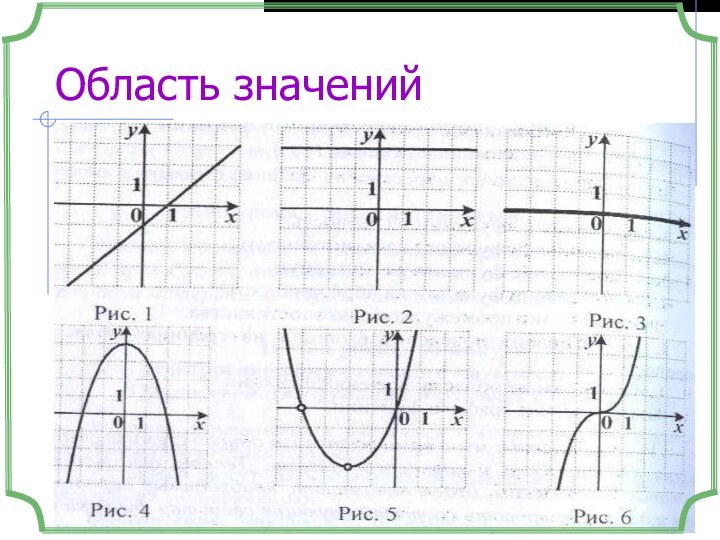
![*Страница Найдите D(f)7. D(f)=(-∞; 0)U(0; +∞)8. D(f)=(-∞; +∞)9. D(f)=(0; +∞)10. D(f)=(-8; 2]11.](/img/tmb/12/1156706/912d7d2d20e1b1a726b586d2a3d7263c-720x.jpg "Функция")
![*Страница 243[0; 5]Функция у = f(x) задана графиком. Укажите множество значений](/img/tmb/12/1156706/9a6b054b18856624807c455df45b8ac9-720x.jpg "Функция")
Слайд 2
*
Страница
Цели урока
Обобщить теоретические знания по теме.
Рассмотреть
Организовать работу учащихся соответственно уровню уже сформированных у них знаний.
Слайд 3
*
Страница
План урока
I этап – организационный
(1 мин.)
II этап – повторение теоретического материала
по теме (20 мин.)III этап – разноуровневая самостоятельная работа (15 мин.)
IV этап – подведение итогов урока, комментарии по домашнему заданию
(4 мин.)
Слайд 4
*
Страница
I этап - организационный
Тема урока: «Определение, способы
задания, свойства, сведённые в общую схему исследования».
Цели урока:
Обобщить теоретические знания по теме.
Рассмотреть решения задач, связанных с этой темой, базового и повышенного уровня.
Слайд 5
*
Страница
II этап – повторение.
Определение функции:
Функцией называется зависимость
переменной у от переменной х, при которой каждому значению
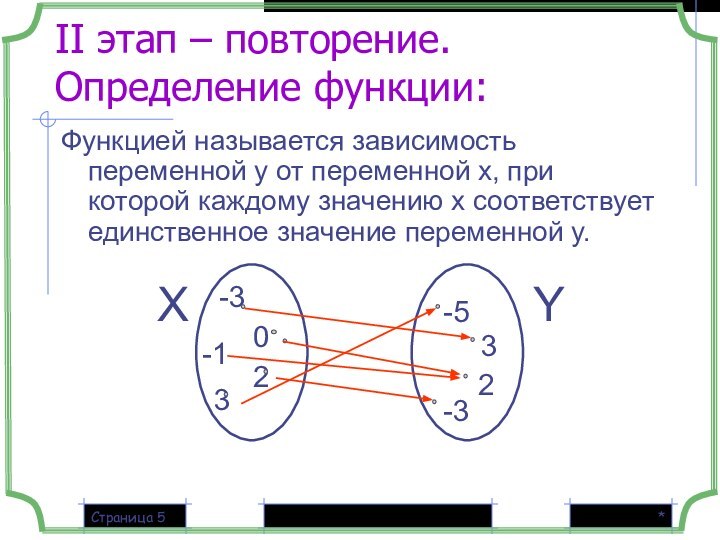
x соответствует единственное значение переменной y.-3
-1
-5
3
2
-3
Y
X
Слайд 9
*
Страница
Способы задания функции
Описательный:
«Каждому двузначному числу поставлен
в соответствие его квадрат»
Табличный
Графический
Аналитический
Слайд 10
*
Страница
Общая схема исследования функции
Область определения функции D(f)
Точки
пересечения графика с осями координат
Чётность, нечётность
Монотонность
Экстремумы
Периодичность
Знакопостоянство
Область значений E(f)
Построение графика
Слайд 11
*
Страница
Область определения функции
- Множество значений независимой переменной,
при которых функция имеет смысл.
Функция – многочлен
Функция задана
в виде дроби Функция задана в виде корня чётной степени
Функция содержит логарифмическое выражение
Композиция функций
Слайд 12
*
Страница
Найдите D(f)
1. D(f)=(-∞; +∞)
2. D(f)=(-∞; +∞)
3. D(f)=(-∞;
+∞)
4. D(f)=(-∞; +∞)
5. D(f)=(-∞; -4)U(-4;-2)U(-2; +∞)
6. D(f)=(-∞; +∞)
Слайд 13
*
Страница
Найдите D(f)
7. D(f)=(-∞; 0)U(0; +∞)
8. D(f)=(-∞; +∞)
9.
D(f)=(0; +∞)
10. D(f)=(-8; 2]
11. НЕ ФУНКЦИЯ
12. D(f)=(-6; 0)U(0; 4]
Слайд 14
*
Страница
Чётность функции
Если область определения функции симметрична относительно
нуля
и для любого х из области определения выполняется равенство
f(-x) = f(x), то функция чётная; и для любого х из области определения выполняется равенство f(-x) = - f(x), то функция нечётная;
Слайд 15
*
Страница
Исследуйте на чётность
1. Ни чётная,
ни нечётная
2.
Чётная
3. Чётная
и нечётная
4. Чётная
6. Нечётная
5. Ни чётная,
ни
нечётная
Слайд 16
*
Страница
Монотонность
Если большему значению аргумента соответствует большее значение
функции, то функция называется монотонно возрастающей x1> x2 и
f(x1) > f(x2)Если большему значению аргумента соответствует меньшее значение функции, то функция называется монотонно убывающей x1> x2 и f(x1) < f(x2)
Слайд 18
*
Страница
Точки экстремума функции
Если в некоторой точке х0
значение функции больше значений функции в окрестности этой точки,
то х0- точка максимума (хmax= х0), а f(х0) – максимум функции (уmax= f(х0) – «гребни функции»)Если в некоторой точке х0 значение функции меньше значений функции в окрестности этой точки, то х0- точка минимума (хmin= х0), а f(х0) – минимум функции (у min = f(х0) – «впадины функции)
Слайд 20
*
Страница
Периодичность функции
Если существует такое число t≠0, что:
для
любого х из области определения функции у=f(x) числа x+t
и x-t принадлежат области определенияи f(x+t) = f(x-t) = f(x),
то функция называется периодической, t - период функции.
Слайд 21
*
Страница
Знакопостоянство функции
Множество Х, на котором функция не
меняет свой знак, называется промежутком знакопостоянства функции
Слайд 22
*
Страница
1 2 3 4
5 6 7 8
-7 -6 -5
-4 -3 -2 -17
6
5
4
3
2
1
-1
-2
-3
-4
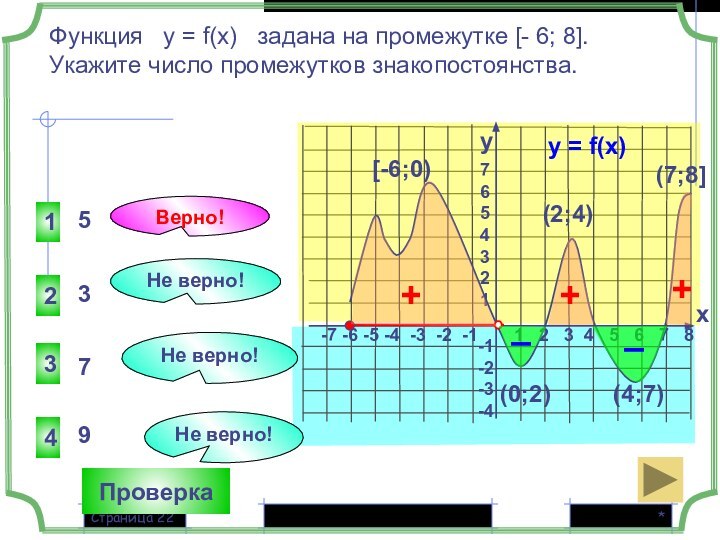
Функция у = f(x) задана на промежутке [- 6; 8].
Укажите число промежутков знакопостоянства.
y
x
у = f(x)
1
3
4
2
Не верно!
Не верно!
Верно!
Не верно!
Проверка
3
5
9
7
Слайд 23
*
Страница
Область значений
Множество, состоящее из всех значений, которые
может принимать функция на своей области определения
Слайд 25
*
Страница
Функция у = f(x) задана графиком. Укажите
область определения этой функции.
Проверка
1 2 3 4
5 6 7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
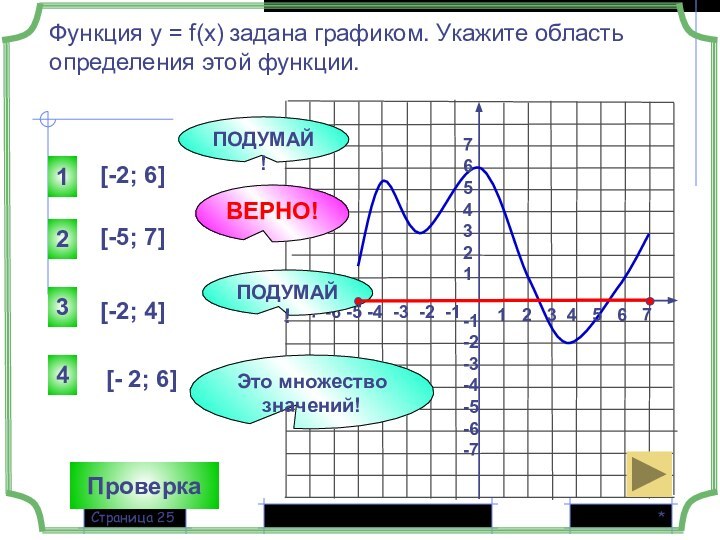
[-2; 6]
[-5; 7]
[-2; 4]
[- 2; 6]
2
1
3
4
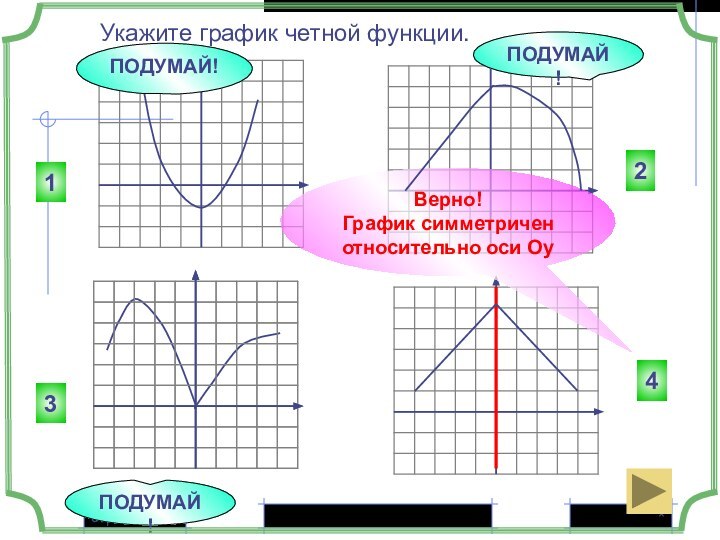
ПОДУМАЙ!
ВЕРНО!
Это множество значений!
ПОДУМАЙ!
Слайд 26
*
Страница
2
4
3
[0; 5]
Функция у = f(x) задана
графиком.
Укажите множество значений этой функции.
Проверка (2)
y = f
(x)
1 2 3 4 5 6 7 8
-7 -6 -5 -4 -3 -2 -1
y
x
5
4
3
2
1
-1
-2
-3
-4
1
[-6; 8]
[-6; 0)
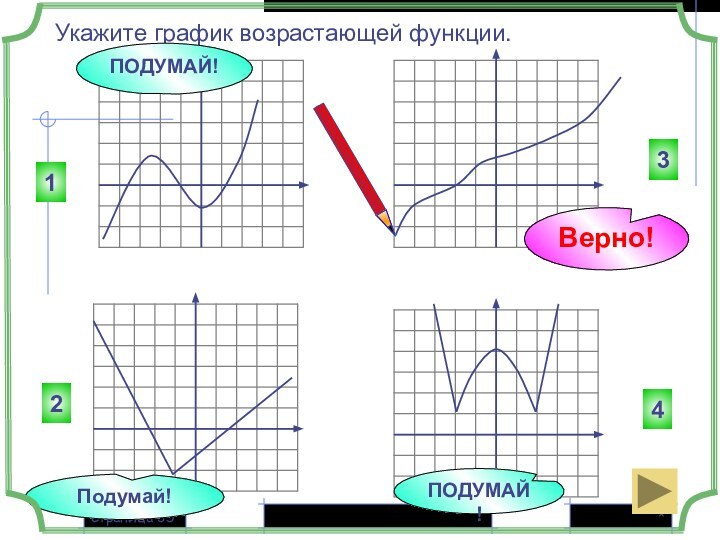
Подумай!
Подумай!
Подумай!
Верно!
Слайд 27
*
Страница
Функция у = f(x) определена графиком. Укажите
промежуток, на котором она принимает только положительные значения.
Проверка
1
2 3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
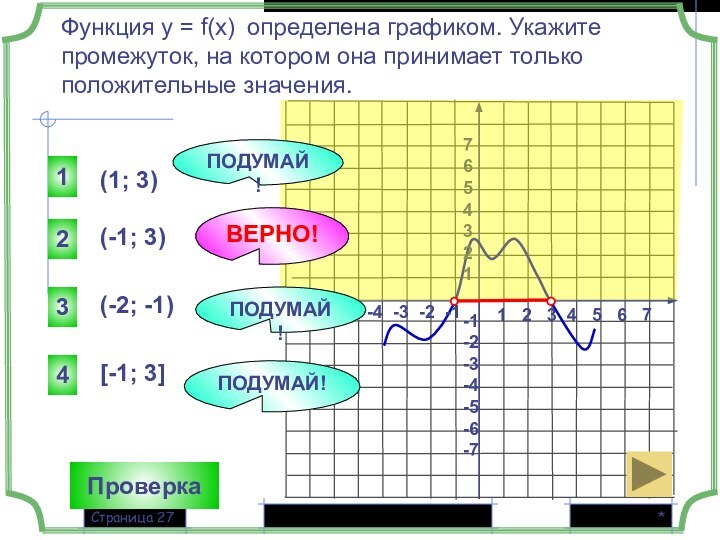
(-1; 3)
2
1
3
4
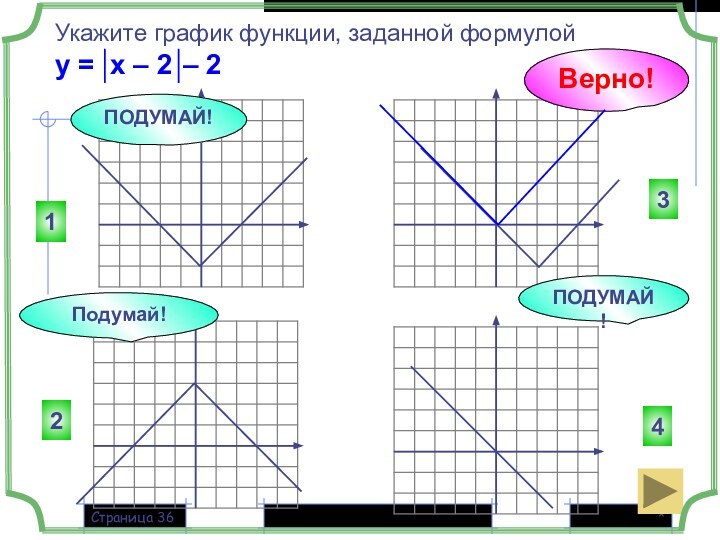
ПОДУМАЙ!
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
(1; 3)
(-2; -1)
[-1; 3]
Слайд 28
*
Страница
Функция у = f(x) задана графиком.
Найдите наибольшее значение функции.
1 2 3 4
5 6 7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
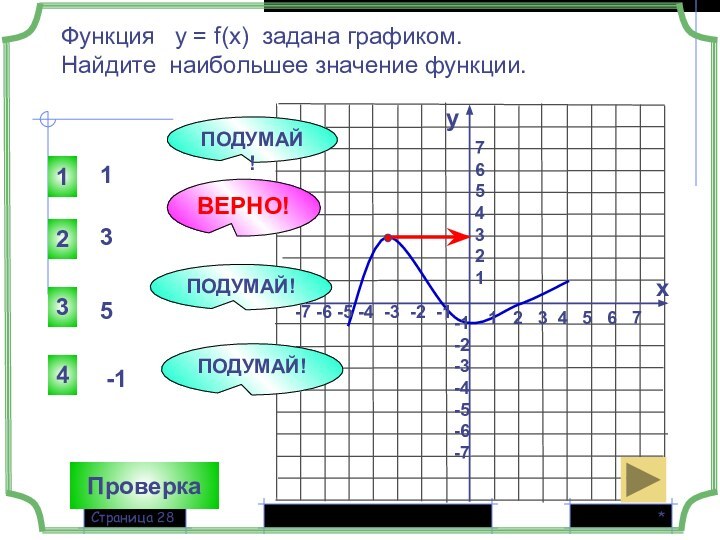
1
3
5
-1
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
у
х
Проверка
Слайд 29
*
Страница
1 2 3 4
5 6 7 8
-7 -6 -5
-4 -3 -2 -17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
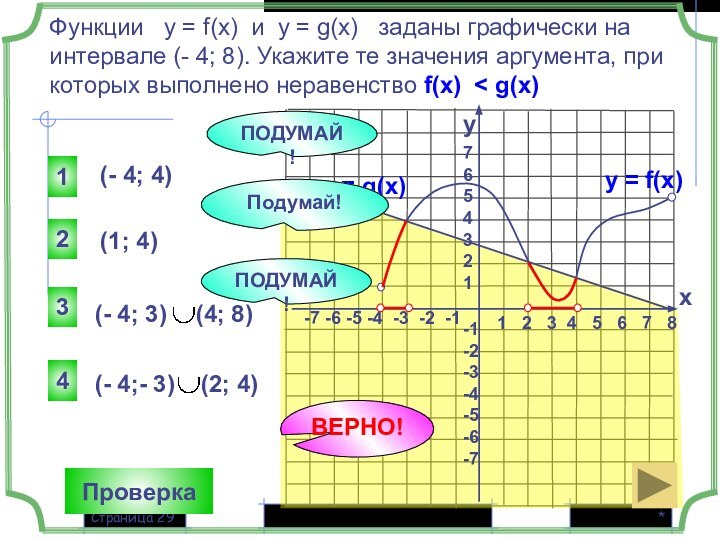
Функции у = f(x) и у = g(x) заданы графически на интервале (- 4; 8). Укажите те значения аргумента, при которых выполнено неравенство f(x) < g(x)
(- 4; 4)
(1; 4)
4
1
3
2
y
x
у = f(x)
у = g(x)
ВЕРНО!
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
Слайд 30
*
Страница
1 2 3 4
5 6 7 8
-7 -6 -5
-4 -3 -2 -17
6
5
4
3
2
1
-1
-2
-3
-4
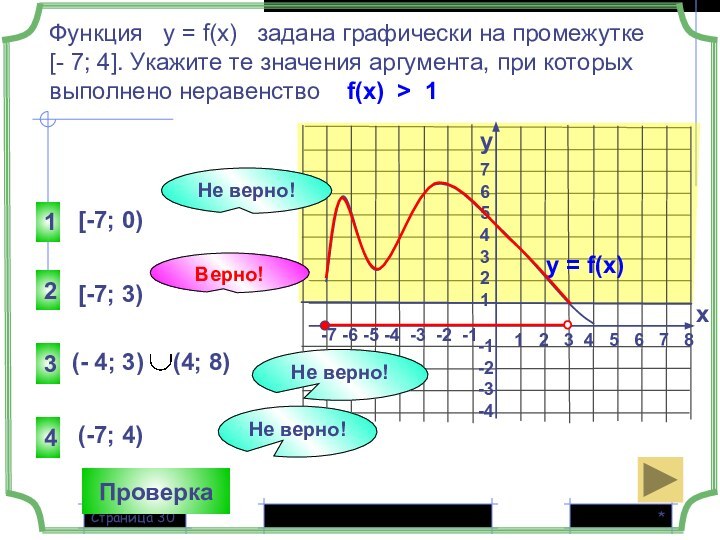
Функция у = f(x) задана графически на промежутке
[- 7; 4]. Укажите те значения аргумента, при которых выполнено неравенство f(x) > 1
y
x
у = f(x)
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
Проверка
[-7; 3)
[-7; 0)
(-7; 4)
Слайд 31
*
Страница
1 2 3 4
5 6 7 8
-7 -6 -5
-4 -3 -2 -17
6
5
4
3
2
1
-1
-2
-3
-4
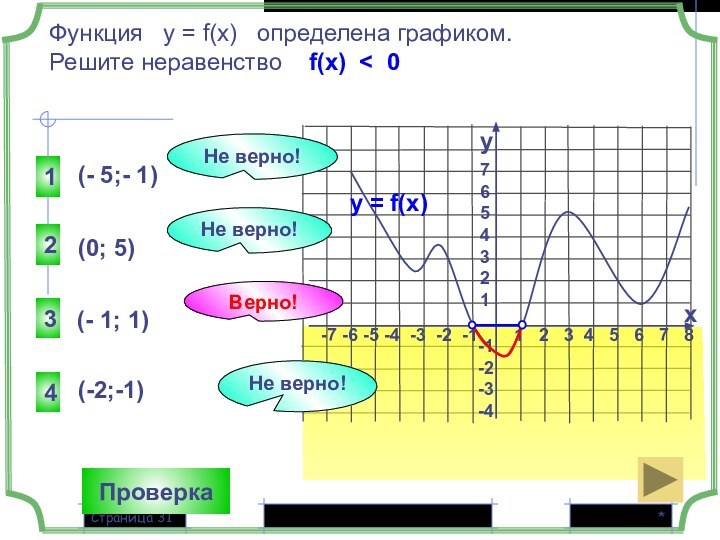
Функция у = f(x) определена графиком.
Решите неравенство f(x) < 0
y
x
у = f(x)
3
2
4
1
Не верно!
Не верно!
Верно!
Не верно!
Проверка
(0; 5)
(- 5;- 1)
(-2;-1)
(- 1; 1)
Слайд 32
*
Страница
1 2 3 4
5 6 7
-7 -6 -5 -4 -3
-2 -17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
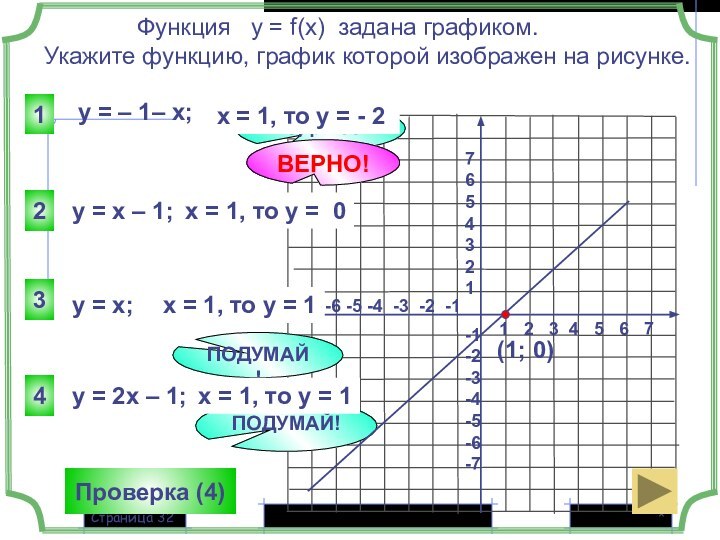
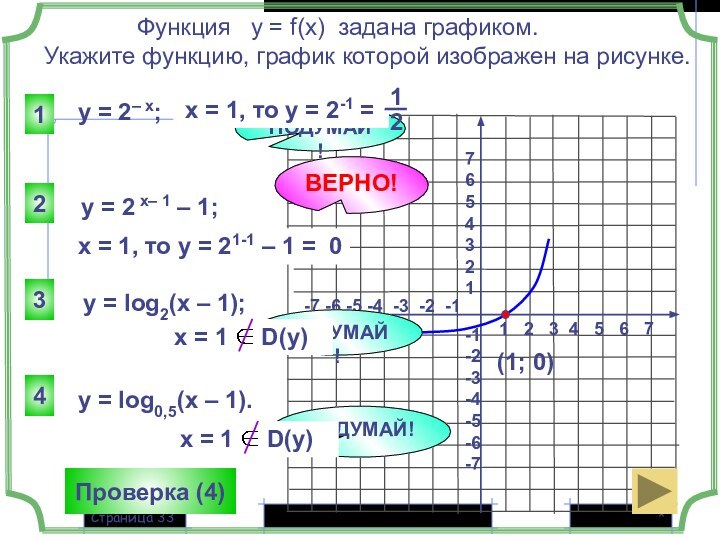
y = – 1– x;
2
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
Функция у = f(x) задана графиком.
Укажите функцию, график которой изображен на рисунке.
ПОДУМАЙ!
x = 1, то у = - 2
x = 1, то у = 0
Проверка (4)
(1; 0)
y = x – 1;
y = x;
y = 2х – 1;
x = 1, то у = 1
ВЕРНО!
x = 1, то у = 1
Слайд 33
*
Страница
1 2 3 4
5 6 7
-7 -6 -5 -4 -3
-2 -17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
y = 2– x;
2
1
3
4
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
Функция у = f(x) задана графиком.
Укажите функцию, график которой изображен на рисунке.
ПОДУМАЙ!
y = 2 x– 1 – 1;
y = log2(x – 1);
y = log0,5(x – 1).
x = 1, то у = 21-1 – 1 = 0
Проверка (4)
(1; 0)
Слайд 34
*
Страница
Укажите график четной функции.
4
2
3
1
ПОДУМАЙ!
ПОДУМАЙ!
Верно!
График симметричен относительно
оси Оу
ПОДУМАЙ!
Слайд 36
*
Страница
Укажите график функции, заданной формулой
у =
х – 2 – 2
3
4
2
1
ПОДУМАЙ!
Подумай!
ПОДУМАЙ!
Верно!
Слайд 37
*
Страница
Функция у =f (x), имеющая период Т
= 4 задана графиком на промежутке [-1; 3].
Найдите
значение этой функции при х = 10. 4
3
1
2
4
1
3
2
Проверка (2)
4
3
2
1
y
–1 1 2 3
Не верно!
Не верно!
Не верно!
Верно!
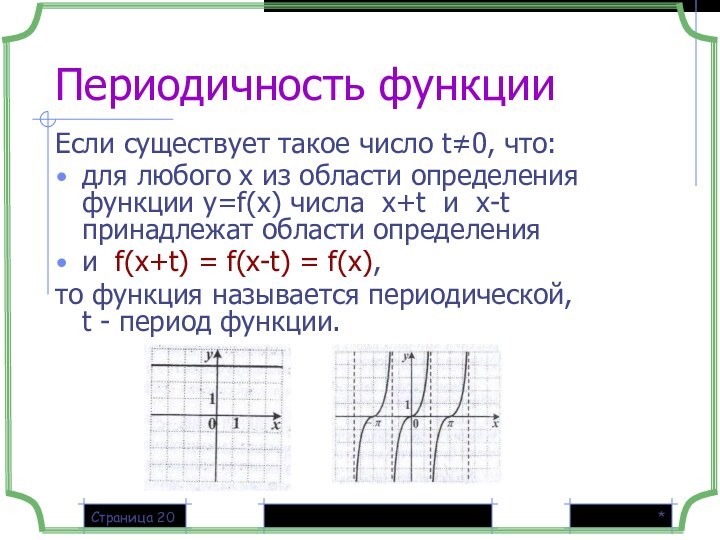
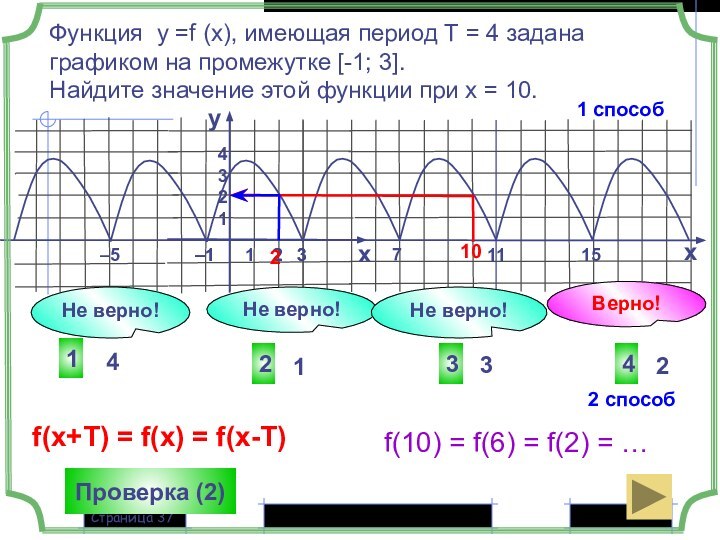
f(x+Т) = f(x) = f(x-T)
f(10) = f(6) = f(2) = …
1 способ
2 способ
10
2
Слайд 38
*
Страница
На рисунке изображен график производной функции
у
=f /(x), заданной на промежутке (- 6; 7). Исследуйте
функцию у =f (x) на экстремум и укажите количество ее точек минимума.1
3
4
2
Не верно!
Не верно!
Верно!
Не верно!
2
3
8
4
Проверка (2)
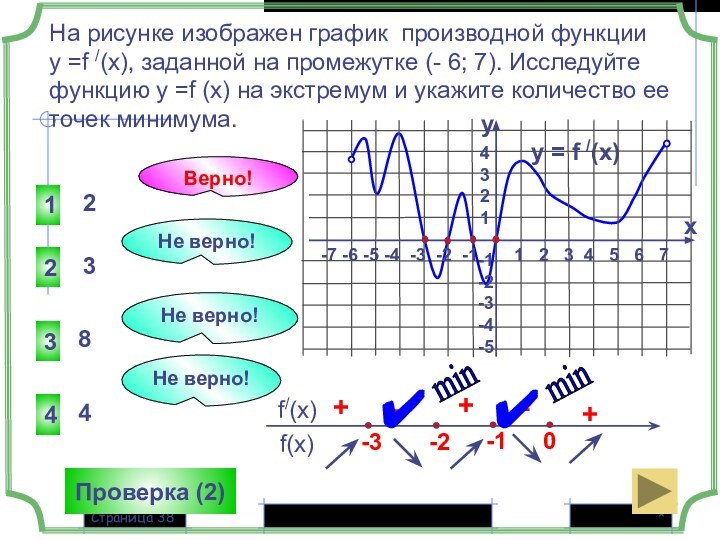
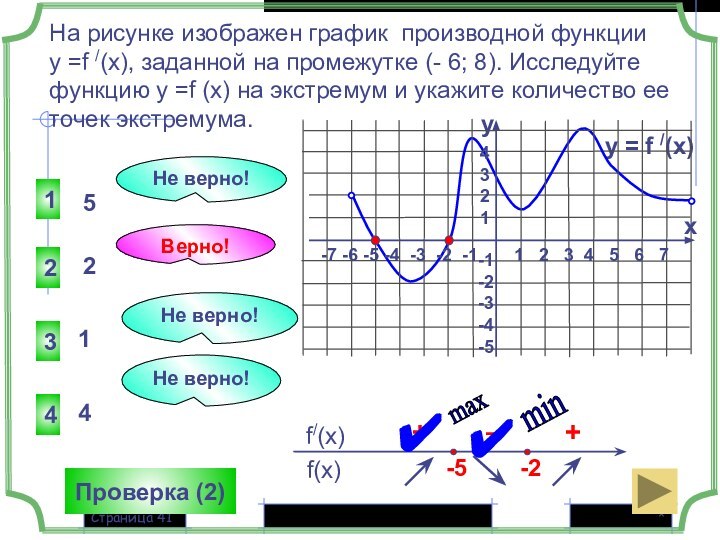
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Слайд 39
*
Страница
На рисунке изображен график производной функции
у
=f /(x), заданной на промежутке (- 6; 8). Исследуйте
функцию у =f (x) на экстремум и укажите количество ее точек максимума.2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
7
3
8
4
Проверка (2)
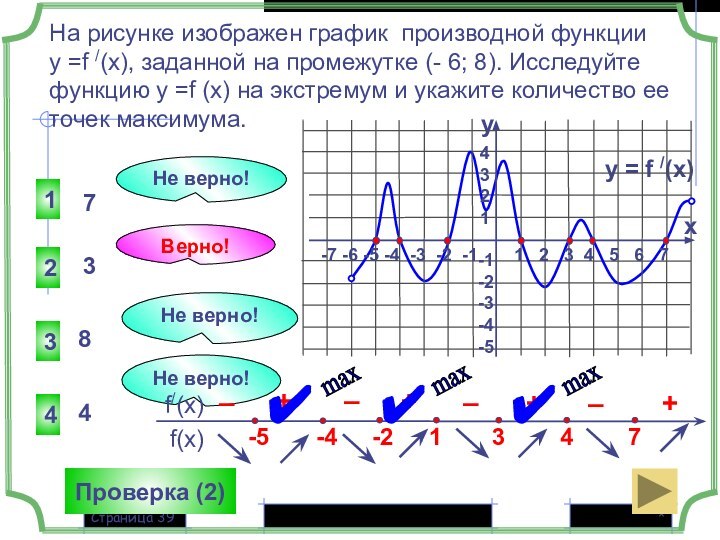
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Слайд 40
*
Страница
На рисунке изображен график производной функции
у
=f /(x), заданной на промежутке (- 5; 5). Исследуйте
функцию у =f (x) на монотонность и укажите число ее промежутков убывания.3
2
4
1
Не верно!
Не верно!
Верно!
Не верно!
3
2
1
4
Проверка (2)
+
–
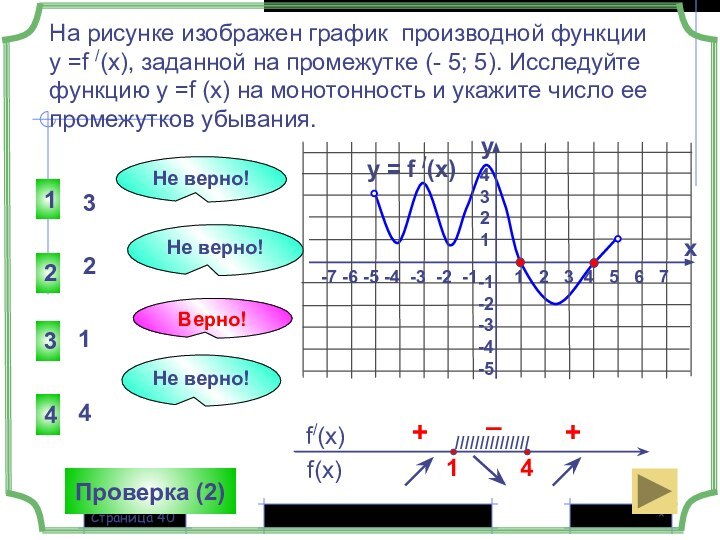
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
IIIIIIIIIIIIIII
Слайд 41
*
Страница
На рисунке изображен график производной функции
у
=f /(x), заданной на промежутке (- 6; 8). Исследуйте
функцию у =f (x) на экстремум и укажите количество ее точек экстремума.2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
5
2
1
4
Проверка (2)
+
–
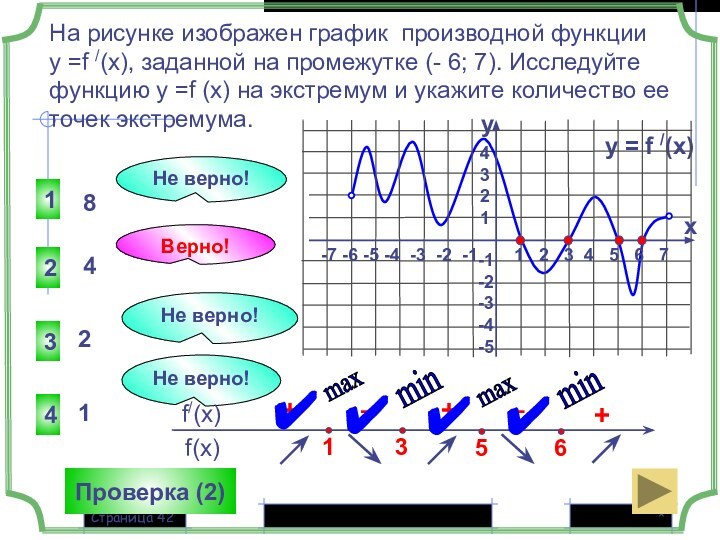
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
Слайд 42
*
Страница
На рисунке изображен график производной функции
у
=f /(x), заданной на промежутке (- 6; 7). Исследуйте
функцию у =f (x) на экстремум и укажите количество ее точек экстремума.2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
8
4
2
1
Проверка (2)
+
–
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
+
Слайд 43
*
Страница
y = f /(x)
1
3
4
2
Не верно!
Не верно!
Не верно!
8
6
4
9
Функция у = f(x) определена на
промежутке на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции.+
–
Верно!
Проверка (2)
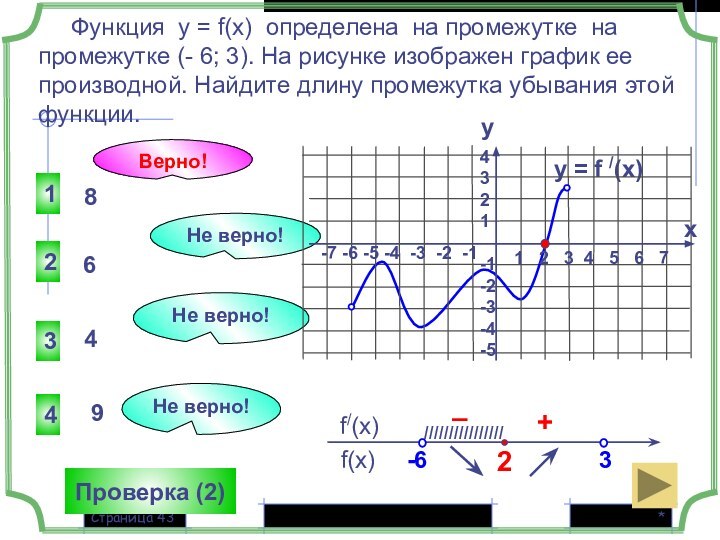
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
IIIIIIIIIIIIIIII
y
x
Слайд 44
*
Страница
y = f /(x)
1 2
3 4 5 х
-4
-3 -2 -1
4
3
1
2
Не верно!
Не верно!
Не верно!
2
- 2
- 4
1
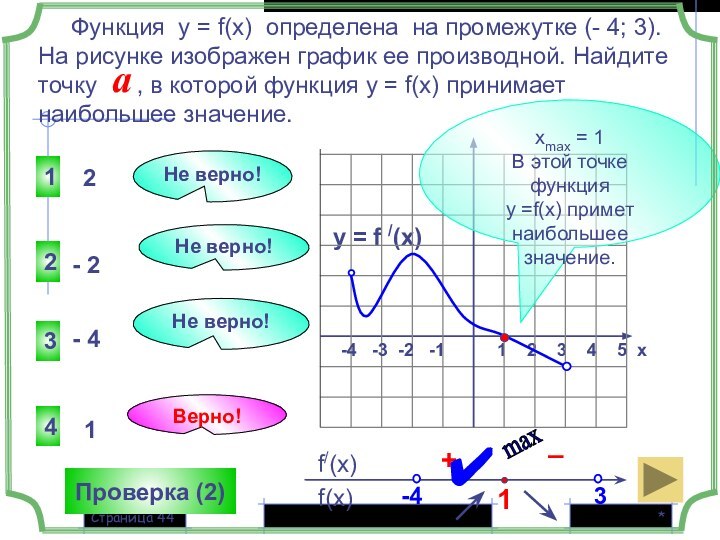
Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. Найдите точку , в которой функция у = f(x) принимает наибольшее значение.
+
–
a
Верно!
Проверка (2)
хmax = 1
В этой точке функция
у =f(x) примет наибольшее значение.
Слайд 45
*
Страница
y = f /(x)
1 2
3 4 5 х
-4
-3 -2 -1
1
3
4
2
Не верно!
Не верно!
Не верно!
2
0
-5
- 3
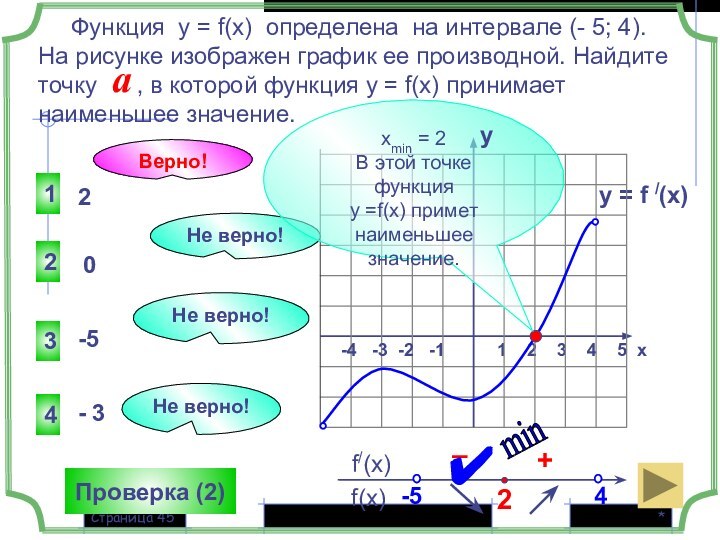
Функция у = f(x) определена на интервале (- 5; 4).
На рисунке изображен график ее производной. Найдите точку , в которой функция у = f(x) принимает наименьшее значение.
+
–
a
хmin = 2
В этой точке функция
у =f(x) примет наименьшее значение.
Верно!
Проверка (2)
y
Слайд 46
*
Страница
III этап. Разноуровневая работа
1 группа – карточки
жёлтые.
2 группа – карточки розовые.
3 группа – разбираем решение
задания:Найдите все значения параметра а, при которых в области определения функции не содержится ни одного двузначного числа
