- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрическая иллюстрация формул сокращенного умножения
Содержание
- 2. «Математика не управляет миром, но показывает, как мир управляется» ГЁТЕ
- 3. Квадрат суммы двух выражений Квадрат суммы двух
- 4. (a+b)²=a²+2ab+b²Площадь квадрата со стороной (a + b) равна(a+b)²a+ba+b
- 5. (a+b)²=a²+2ab+b²Разобьём этот квадрат на два квадрата и два равных прямоугольникаab
- 6. (a+b)²=a²+2ab+b² Определим площадь каждой из этих фигурa²b²abab
- 7. (a+b)²=a²+2ab+b² Площадь квадрата равна
- 8. Получили(a+b)²=a²+2ab+b²
- 9. Квадрат разности двух выражений. Квадрат разности двух
- 10. (a-b)²=a²-2ab+b² Площадь квадрата со стороной a равна
- 11. (a-b)²=a²-2ab+b² Отложим на каждой стороне квадрата отрезок b, получим: два квадрата и два равных прямоугольникаb(a-b)²b²a-bba-bb
- 12. (a-b)²=a²-2ab+b²Найдем площадь квадрата и одного из прямоугольников S₁= abs₂ = aba(a-b)²bb²bS₁S₂aa
- 13. (a-b)²=a²-2ab+b²Если мы из площади большого квадрата вычтем
- 14. (a-b)²=a²-2ab+b²Значит, её нужно прибавитьab(a-b)²b²abab
- 15. (a-b)²=a²-2ab+b²Квадрат розового цвета имеет ребро
- 16. Получили(a-b)²=a²-2ab+b² и (a-b)²=a²-2ab+b²
- 17. Скачать презентацию
- 18. Похожие презентации
«Математика не управляет миром, но показывает, как мир управляется» ГЁТЕ















Слайд 3 Квадрат суммы двух выражений Квадрат суммы двух выражений равен
квадрату первого выражения плюс удвоенное произведение первого на второго
и плюс квадрат второго выражения
(a + b)² = а² +2 а b + b²
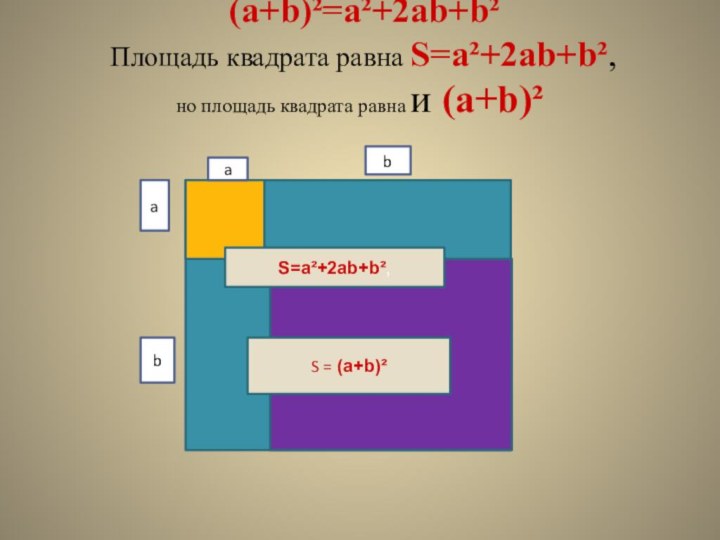
Слайд 7 (a+b)²=a²+2ab+b² Площадь квадрата равна S=a²+2ab+b², но площадь квадрата
равна и (a+b)²
S=a²+2ab+b²,
S = (a+b)²
a
b
a
b
Слайд 9 Квадрат разности двух выражений. Квадрат разности двух выражений равен
квадрату первого выражения минус удвоенное произведение первого на второе
и плюс квадрат второго выражения (a-b)²=a²-2ab+b²
Слайд 11
(a-b)²=a²-2ab+b²
Отложим на каждой стороне квадрата отрезок b, получим:
два квадрата и два равных прямоугольника
b
(a-b)²
b²
a-b
b
a-b
b
Слайд 12
(a-b)²=a²-2ab+b²
Найдем площадь квадрата и одного из прямоугольников
S₁= ab
s₂ = ab
a
(a-b)²
b
b²
b
S₁
S₂
a
a
Слайд 13
(a-b)²=a²-2ab+b²
Если мы из площади большого квадрата вычтем сумму
s₁ и s₂, то мы дважды вычтем площадь темного
квадрата.
Слайд 15
(a-b)²=a²-2ab+b²
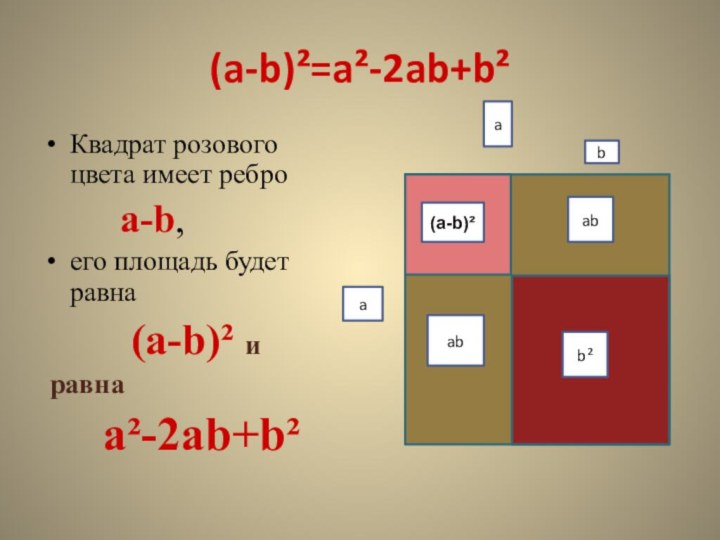
Квадрат розового цвета имеет ребро
a-b,
его площадь будет равна
(a-b)² иравна
a²-2ab+b²
(a-b)²
b²
ab
ab
a
a
b