- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Понятие о производной (11 класс)
Содержание
- 2. Задачи, приводящиек понятию производной1. Задача о
- 3. Дадим аргументу x0 приращение Δx и перейдем
- 5. Уравнение прямой, проходящей через точку M0 имеет вид:Рассмотрим прямоугольный треугольник M0M1N:- угловой коэффициент секущей M0M1.
- 6. Тогда угловой коэффициент касательной к кривой в точке M0 :
- 7. 2. Задача о скоростидвиженияПусть вдоль некоторой прямой
- 8. Тогда за промежуток времени Δt средняя скорость
- 9. Поэтому под скоростью точки в момент времени t0 понимают:
- 10. 3. Задача о производительноститрудаПусть функция u=u(t) выражает
- 11. Тогда за промежуток времени Δt средняя производительность
- 12. Скачать презентацию
- 13. Похожие презентации
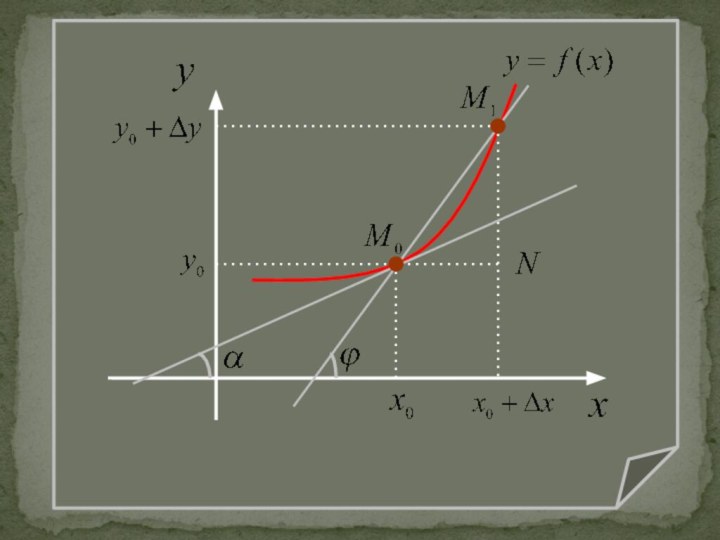
Задачи, приводящиек понятию производной1. Задача о касательнойПусть на плоскости XOY задана непрерывная кривая y=f(x). Необходимо найти уравнение касательной к этой кривой в точке M0(x0,y0).











Слайд 2
Задачи, приводящие
к понятию производной
1. Задача о касательной
Пусть
на плоскости XOY задана непрерывная кривая y=f(x).
уравнение касательной к этой кривой в точке M0(x0,y0).Слайд 3 Дадим аргументу x0 приращение Δx и перейдем на
кривой от точки M0(x0, f(x0)) к точке M1(x0+Δx, f(x0+
Δx)).Проведем секущую M0M1.
Под касательной к кривой y=f(x) в точке
M0 (x0 ,y0 ) понимают предельное положение
секущей M0 M1 при приближении точки M1
к точке M0 , т.е. при
Слайд 5
Уравнение прямой, проходящей через точку M0 имеет вид:
Рассмотрим
прямоугольный треугольник M0M1N:
- угловой коэффициент секущей M0M1.
Слайд 7
2. Задача о скорости
движения
Пусть вдоль некоторой прямой движется
точка по закону S=S(t), где S – пройденный путь,
t – время движения.Требуется найти скорость в момент времени t0 .
Слайд 8
Тогда за промежуток времени Δt средняя скорость составит:
Чем
меньше Δt, тем лучше средняя скорость характеризует движение в
момент t0.На момент времени t0 пройденный путь составит S0=S(t0), на момент времени t0+Δt пройденный путь составит S0+ΔS=S(t0 +Δt ).
Слайд 10
3. Задача о
производительности
труда
Пусть функция u=u(t) выражает количество
произведенной продукции u за время t.
Требуется найти производительность труда
в момент времени t0 .Слайд 11 Тогда за промежуток времени Δt средняя производительность труда
составит:
Чем меньше Δt, тем лучше средняя производительность труда характеризует
производительность в момент t0.За период от t0 до t0+Δt количество произведенной продукции изменится от u0=u(t0) до u0+Δu=u(t0 +Δt ).