может. Занятия математикой – это такая гимнастика ума, для
которой нужны вся гибкость и вся выносливость молодости.Норберт Винер (1894-1964),
американский ученый
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть























IV век до н.э., Евклид, V книга «Начал»: если a, b, c, d – положительные числа и a – наибольшее число в пропорции a/b=c/d, то выполняется неравенство a+d=b+c.
III век , основной труд Паппа Александрийского «Математическое собрание»: если a, b, c, d – положительные числа и a/b>c/d,
то выполняется неравенство ad>bc.
Более 2000 лет до н.э. было известно неравенство
Обращается в верное равенство при a=b.
1631 год. Введены знаки > и < английским ученым Харритом в книге «Практика аналитического искусства».
1734 год. Знаки введены французским математиком П.Буге.
Алгебраические
Метод расщепления
для нестрогих неравенств
Два неравенства называются равносильными, если все решения каждого являются решениями другого неравенства или оба неравенства решений не имеют.
Неравенства
Решением неравенства с одной переменной
5) Записываем ответ.
2. Построим схематически графики обеих функций,
проходящие через точку с найденной абсциссой;
3. Выберем решение неравенства, соответствующее
знаку неравенства;
4. Запишем ответ.
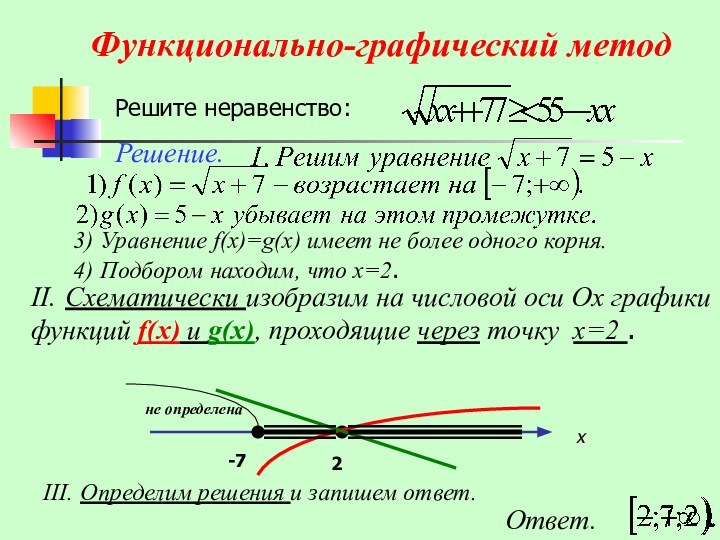
III. Определим решения и запишем ответ.
Ответ.
х
-7
не определена
2