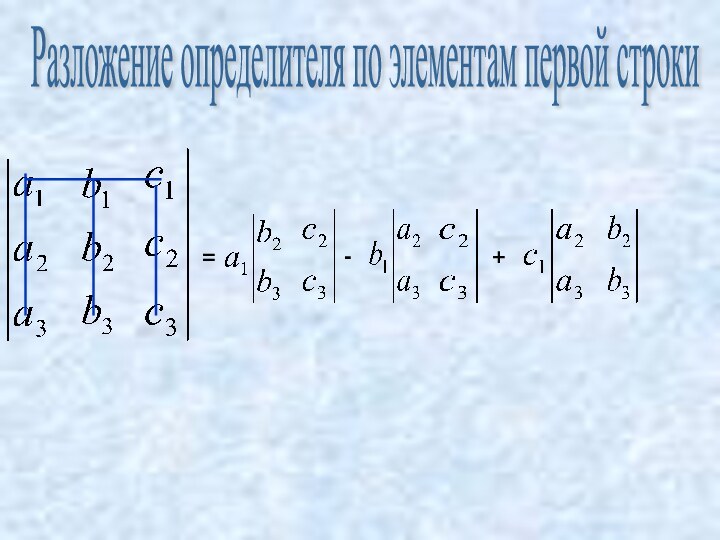
систем линейных алгебраических уравнений.
Задачи исследования:
рассмотрение схем вычисления
определителей и их свойств;решение систем линейных алгебраических уравнений и некоторых задач аналитической геометрии с помощью определителей.