и С.
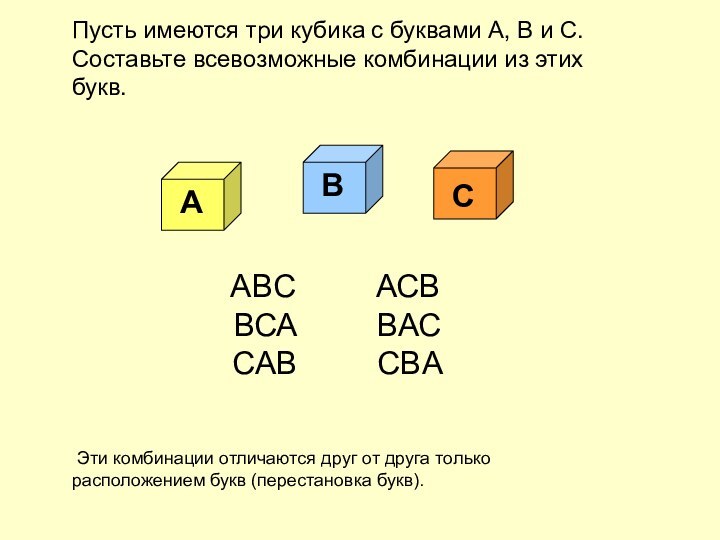
Составьте всевозможные комбинации из этих букв.
ABC
АСВ ВСА ВАС
CAB CBA
Эти комбинации отличаются друг от друга только расположением букв (перестановка букв).
А
В
С
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













А
В
С
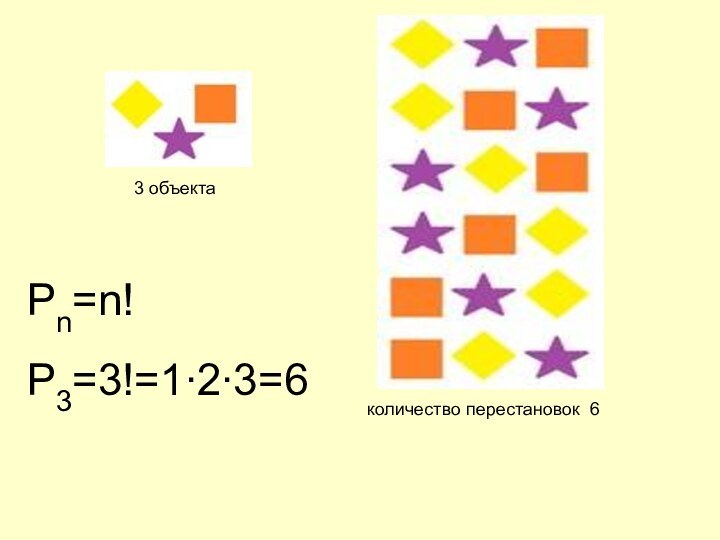
Формула перестановки:
Рn=n!
При перестановке число объектов остается неизменными,
меняется только их порядок
С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно.
Р10 =10! = = 1*2*3*4*5*6*7*8*9*10 = 3628800
Ответ: 3628800
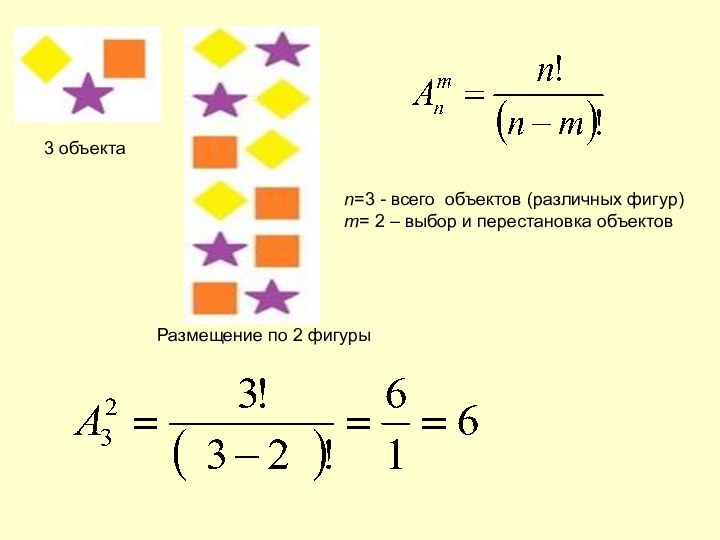
При размещениях меняется и состав выбранных объектов, и их порядок.
Формула размещения:
Ответ: 2520 способов
Ответ: 60 чисел
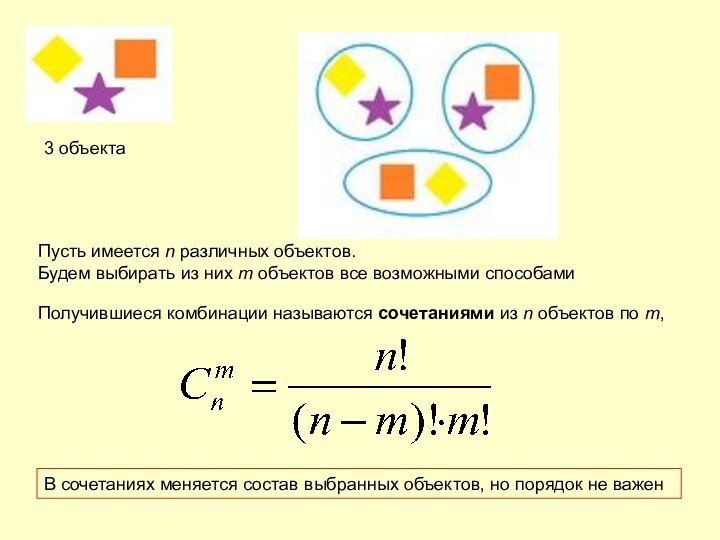
В сочетаниях меняется состав выбранных объектов, но порядок не важен
Ответ: 10 способов.
Ответ: 190