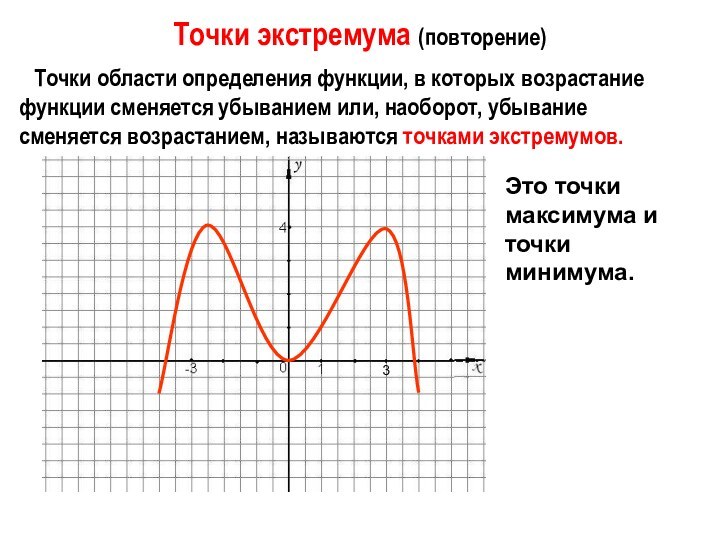
в которых возрастание функции сменяется убыванием или, наоборот, убывание
сменяется возрастанием, называются точками экстремумов.Это точки максимума и точки минимума.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

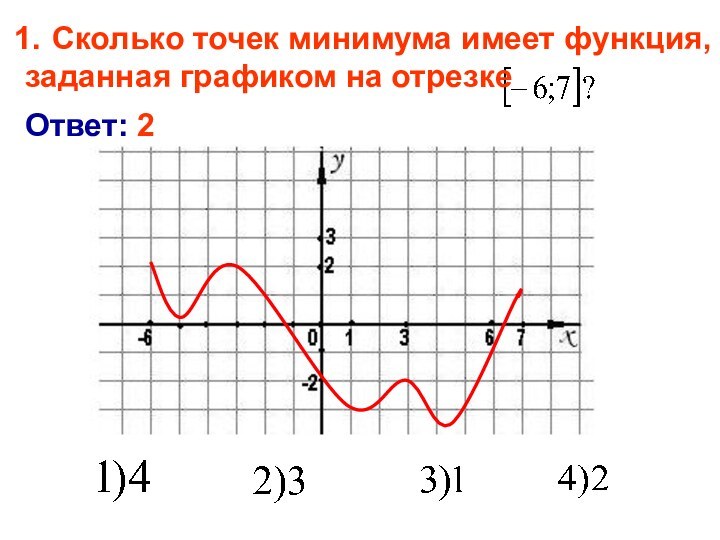

Это точки максимума и точки минимума.
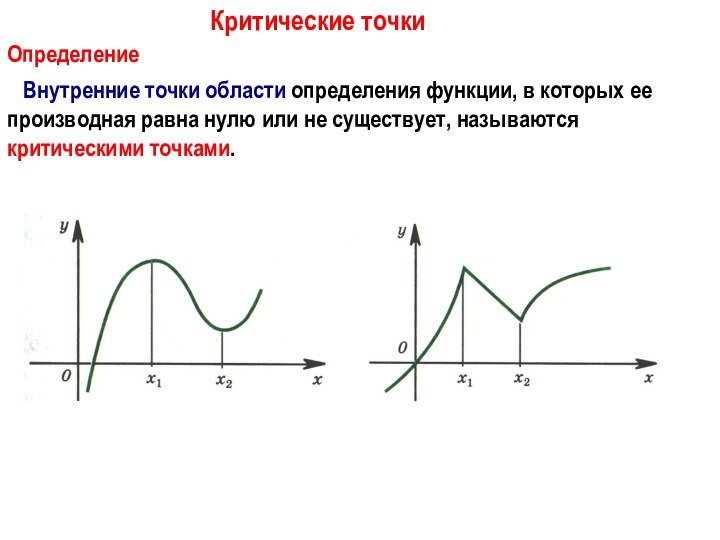
Критические точки
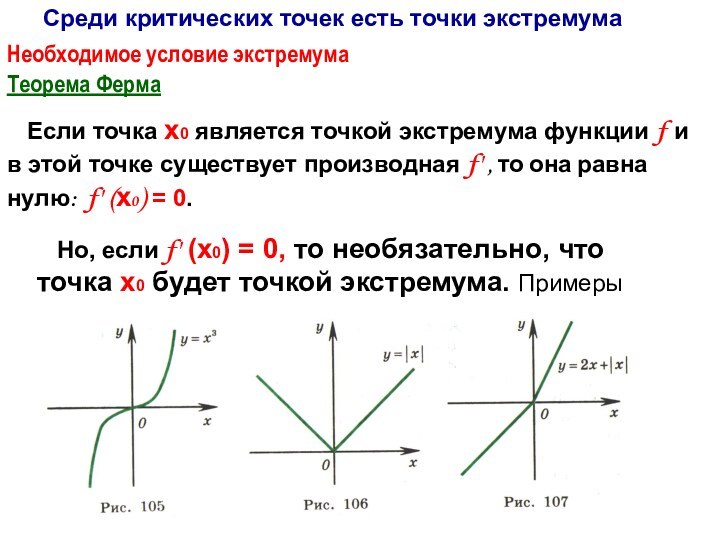
Среди критических точек есть точки экстремума
Необходимое условие экстремума
Но, если f' (х0) = 0, то необязательно, что точка х0 будет точкой экстремума. Примеры
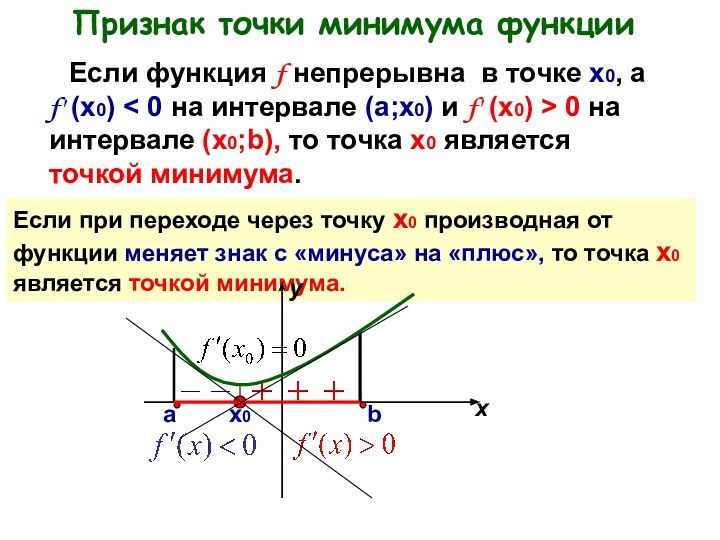
Если при переходе через точку х0 производная от функция меняет знак с «плюса» на «минус», то точка х0 является точкой максимума.
х0
х
y
а
b