Слайд 2
Цель: Знакомство с различными способами решения квадратных уравнений.
Задачи:
Познакомиться с устными способами
решения квадратных уравнений.
Рассмотреть нестандартные способы решения квадратных уравнений.
Расширить кругозор учащихся.
Повысить интерес к истории математики, к предмету.
Слайд 3
Какое уравнение называют квадратным?
Квадратным уравнением называют алгебраическое
уравнение второй степени вида
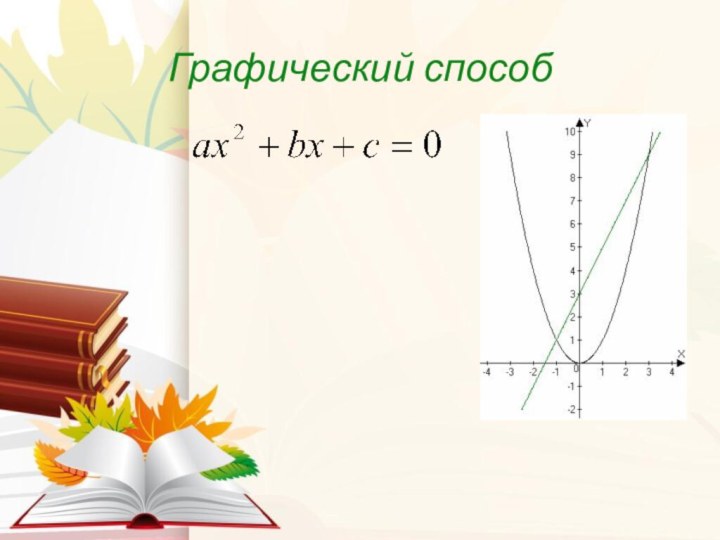
,
где x – переменная,
a, b, c - действительные числа.
Слайд 4
Виды квадратных уравнений
Неполные квадратные уравнения.
Неполным квадратным уравнением называют
квадратное уравнение, в котором коэффициент b или свободный член
c равен нулю.
Виды неполных квадратных уравнений:
Слайд 5
Виды квадратных уравнений
Приведенные квадратные уравнения.
Приведенным квадратным уравнением называется уравнение вида
Слайд 9
Решение квадратных уравнений по формулам
Корни квадратного уравнения вида
находятся по формуле
Слайд 10
Зависимость количества корней от знака дискриминанта
Слайд 11
Решение квадратных уравнений с помощью номограммы.
Номограмма- графическое
представление функции от нескольких переменных, позволяющее с помощью простых
геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений.
С помощью номограммы можно решить только приведенные уравнения, общая формула таких уравнений:
x2+px+q=0
Слайд 12
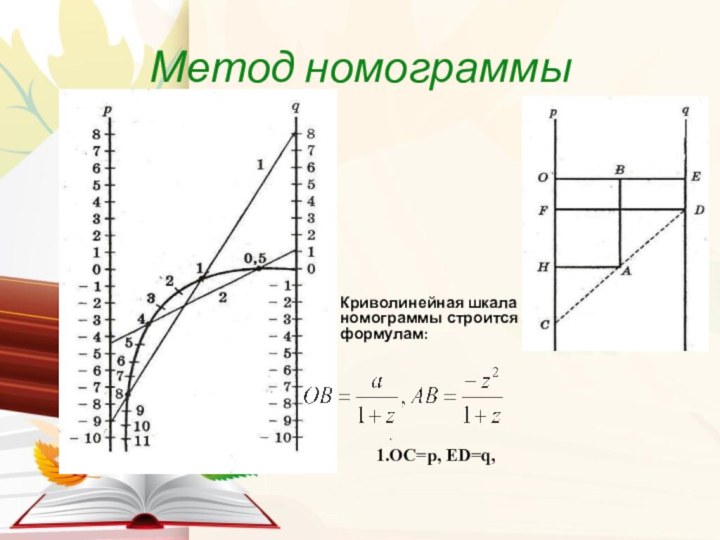
Метод номограммы
Криволинейная шкала номограммы строится по формулам:
.
OC=p, ED=q,
Слайд 13
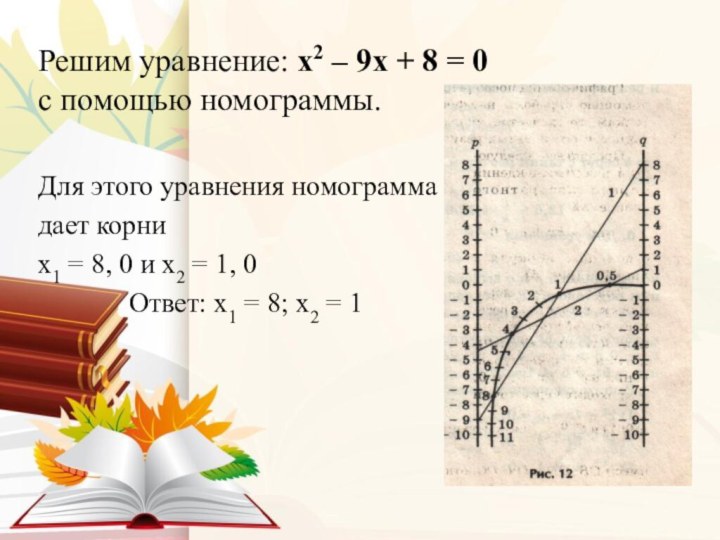
Решим уравнение: x2 – 9x + 8 =
0 с помощью номограммы.
Для этого уравнения номограмма
дает корни
x1 = 8, 0 и x2 = 1, 0
Ответ: x1 = 8; x2 = 1
Слайд 14
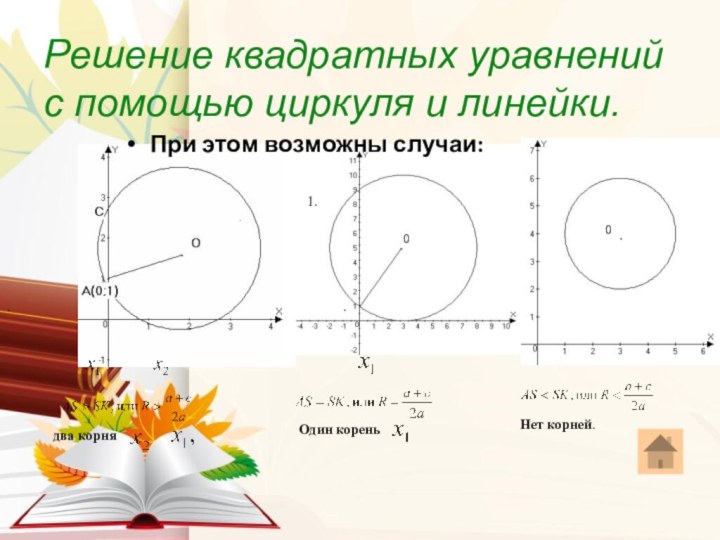
Решение квадратных уравнений с помощью циркуля и линейки:
Центр
окружности О(х;у):
Точка А (0;1)
Слайд 15
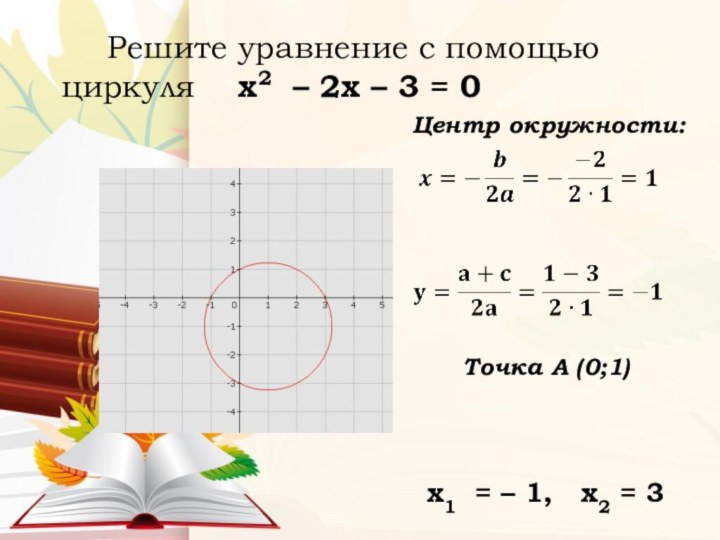
Решите уравнение с помощью циркуля х2
– 2х – 3 = 0
х1 = – 1, х2 = 3
Центр окружности:
Точка А (0;1)
Слайд 16
Решение квадратных уравнений с помощью циркуля и линейки.
0
0
1.
два корня
.
Один корень
.
Нет корней.
При
этом возможны случаи:
Слайд 17
Решения квадратных уравнений способом «переброски»
Рассмотрим квадратное уравнение
ах2
+ bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х =
тогда приходим к уравнению
у2 + by + ас = 0,
равносильного данному.
Слайд 18
Ответ:x1=3 ; x2=2,5
Решим уравнение 2х2 – 11х +
15 = 0 .
Решение. «Перебросим» коэффициент 2 к свободному
члену, в результате получим уравнение
у2 – 11y +30 = 0.
D=b2-4ac=(-11)2-4*30=121-120=1
y1=(-b+√D)/2a=(-(-11)+1)/2*1=12/2=6
y2=(-b-√D)/2a=(-(-11)-1)/2*1=10/2=5
x1=y1/2=6/2=3
x2=y2/2=5/2=2,5
Слайд 19
Теорема Виета
Сумма корней приведенного квадратного
уравнения равна второму коэффициенту, взятому с противоположным знаком, тогда
и только тогда, когда произведение корней равно свободному члену.
Слайд 20
Свойства коэффициентов квадратного уравнения
Если в уравнении
, где a 0 ; ( то есть сумма коэффициентов равна нулю), то:
Пример
Дано уравнение
Так как a + b + c=0, 45+(-23)+(-22)=0, то
Слайд 21
Свойства коэффициентов квадратного уравнения
Если
, или , то
Пример
Дано уравнение
Так как , 2005=2008-3, то
Слайд 22
Свойства коэффициентов квадратного уравнения
Если
то x=-a,x=
Пример
Дано уравнение
Так как 7=7, 50=49+1, то
a
- 1
2
1
Слайд 23
Свойства коэффициентов квадратного уравнения
Если
, то
Пример
Дано уравнение
Так как 11=11, 122=121+1, то
Квадратные уравнения играют огромную роль в развитии математики.
Научиться решать их должен каждый. Использование какого-либо способа зависит от индивидуальных особенностей человека, от его теоретической подготовки.