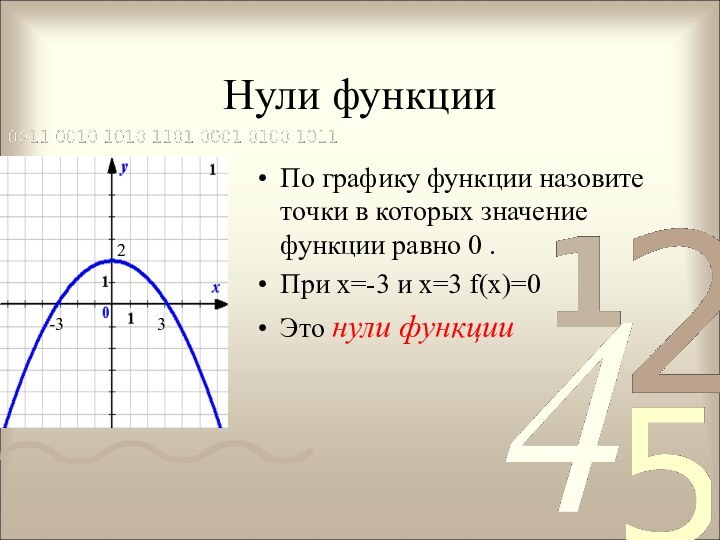
значение функции равно 0 .
При х=-3 и х=3 f(x)=0
Это
нули функции3
-3
2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

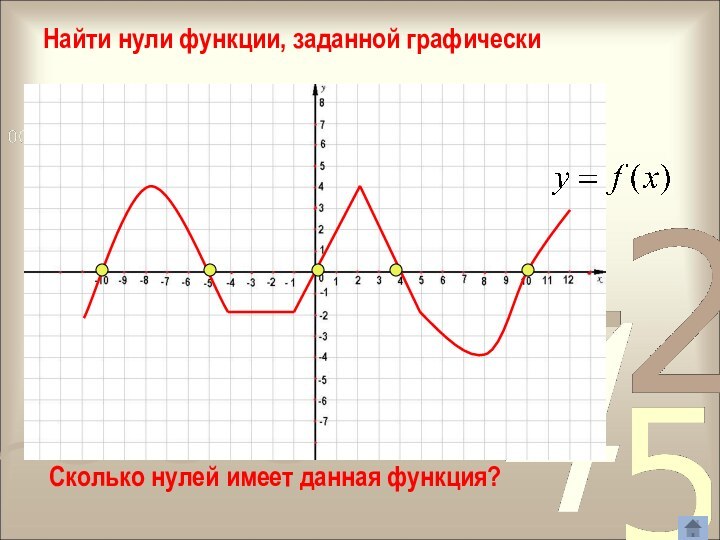
















3
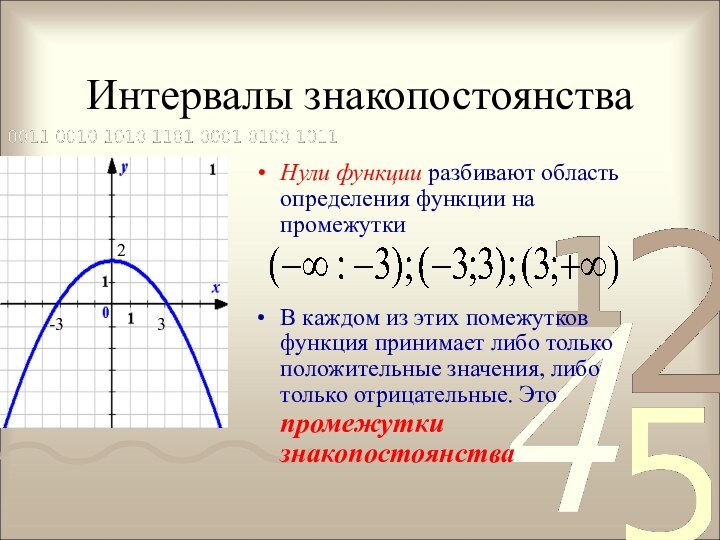
-3
2
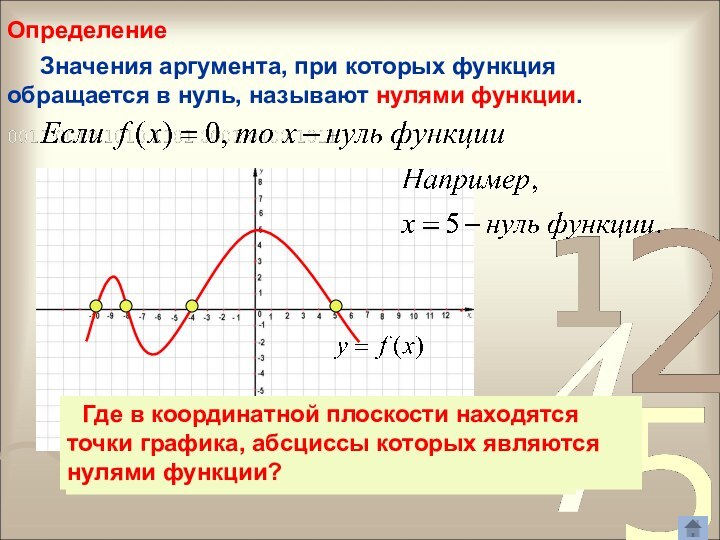
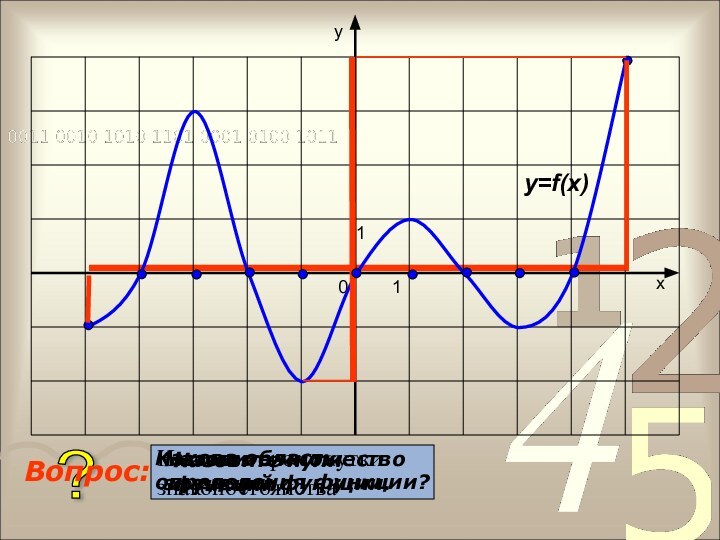
Где в координатной плоскости находятся точки графика, абсциссы которых являются нулями функции?
3
-3
2
у
х
о
y=f(x)
y
x
o
y=f(x)
Функция возрастает, если большему (меньшему) значению аргумента соответствует большее (меньшее) значение функции.
Функция убывает, если большему (меньшему) значению аргумента соответствует меньшее (большее) значение функции.
Определение 2.
Функция у = f (х) называют убывающей на промежутке Х, если из неравенства х1 < х2, где х1 и х2 – любые две точки промежутка Х, следует неравенство f (х1) > f (х2).
у
х
у
х
о
о
х1
х2
х1
х2
f (x1)
f (x2)
f (x2)
f (x1)
у
х
о
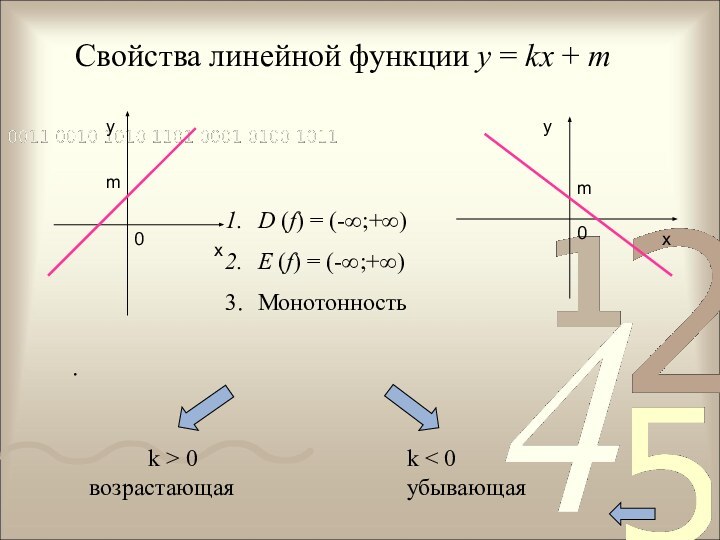
у=kx+m,k>0
у
х
о
у=kx+m,k<0
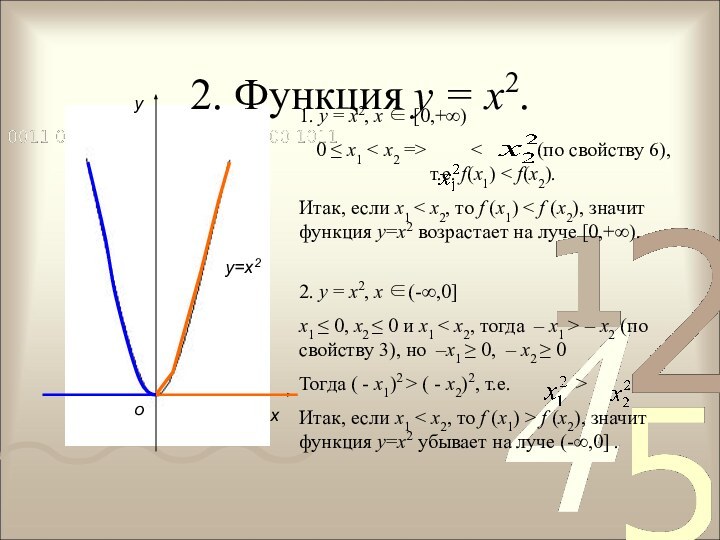
2. у = х2, х ∈(-∞,0]
х1 ≤ 0, x2 ≤ 0 и х1 < х2, тогда – х1 > – х2 (по свойству 3), но –х1 ≥ 0, – х2 ≥ 0
Тогда ( - х1)2 > ( - х2)2, т.е. > .
Итак, если х1 < х2, то f (x1) > f (x2), значит функция у=х2 убывает на луче (-∞,0] .
Итак, если х1 < х2, то f (x1) > f (x2), значит функция убывает на открытом луче (0,+∞)
2. Пусть у = f (x), где , х ∈(- ∞,0)
x1 < 0, x2 < 0 и x1 < x2, тогда – x1 > – x2 =>
< => > , т.е. f (x1) > f (x2)
Итак, если х1 < х2, то f (x1) > f (x2), значит функция убывает на открытом луче (- ∞;0)
m
m
.
Функция возрастает на промежутках (-∞;0) и (0;+∞)
х
х
у
у
0
0
x
y
0
3. Промежутки монотонности
убывает на луче (-∞;0], возрастает на луче [0;+∞)
2. Е (f) = [0;+∞)
2. Е (f) = (-∞;0]
x
y
0
убывает на луче [0;+∞), возрастает на луче (-∞;0]