- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Графическое решение квадратных уравнений
Содержание
- 2. «Математика» - знание, наука. Именно поэтому, если
- 3. «Математику нельзя изучать, наблюдая, как это делает сосед!»А. Нивен
- 4. Цели урока:1. Образовательные: познакомить учащихся с графическим
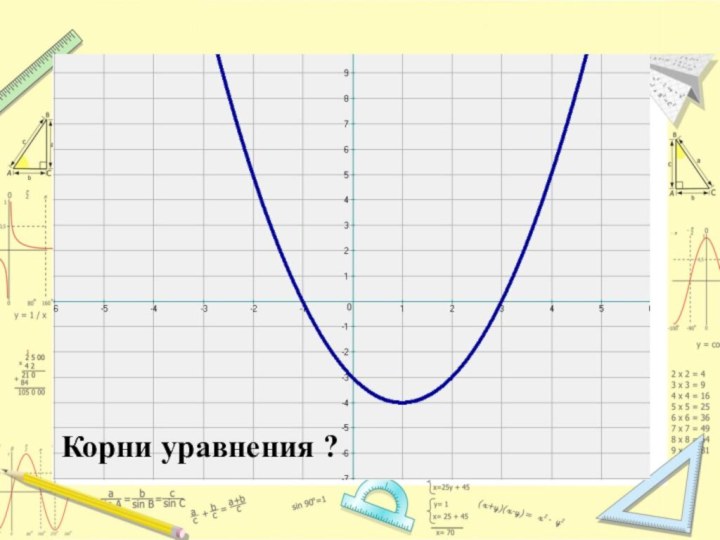
- 7. Решить уравнение х2-2х-3=0
- 8. Корни уравнения ?
- 9. Квадратное уравнение (общий вид)ax2 + bx + c=0где а, b, с-любые числа (коэффициенты), причём а≠0.
- 10. «Человеку, изучающему алгебру, часто полезнее решить одну
- 11. Способы графического решения квадратного уравнения
- 12. Алгоритм решения квадратного уравнения графическим способомПостроить график
- 13. 3-1Построим график функции х2-2х-3=01. График-парабола, а=1>0,ветви
- 14. Алгоритм решения квадратного уравнения графическим способомСпособ 2
- 15. x2 – 2x – 3 =0
- 16. Алгоритм решения квадратного уравнения графическим способомСпособ 3
- 17. x2 – 2x – 3 =0
- 18. Преобразовать уравнение к виду a(x + l)2
- 19. x2 – 2x – 3 =0
- 20. x2 – 2x = 3Прибавим к левой
- 21. Преобразовать уравнение к виду с/х = -
- 22. x2 – 2x – 3 =0
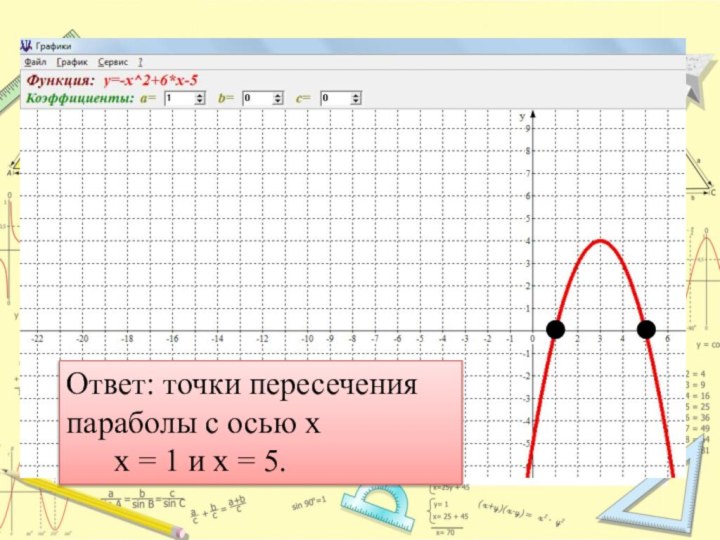
- 23. Решите графически уравнение-х2 + 6х - 5=0
- 24. Ответ: точки пересечения параболы с осью х х = 1 и х = 5.
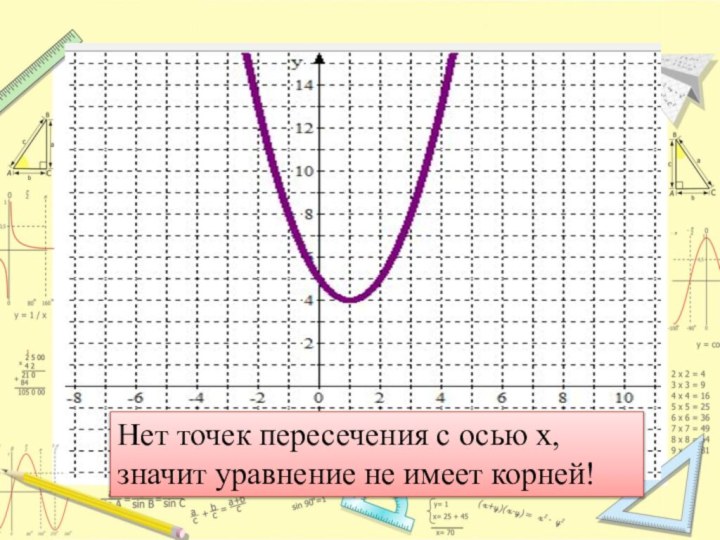
- 25. х2-2х+8=0Решите графически уравнение
- 26. Нет точек пересечения с осью х, значит уравнение не имеет корней!
- 27. I космическая скорость: 7,91 км/с
- 28. II космическая скорость 11,2 км/с
- 29. III космическая скорость 16,6 км/с
- 30. График успеваемости 8 класса
- 31. График роста, веса 8 класса
- 32. Домашнее задание§ 23 c.127-131, № 23.4-23.8 (все
- 33. зелёным – урок понравился, все понялжёлтым –
- 34. Скачать презентацию
- 35. Похожие презентации
























Слайд 4
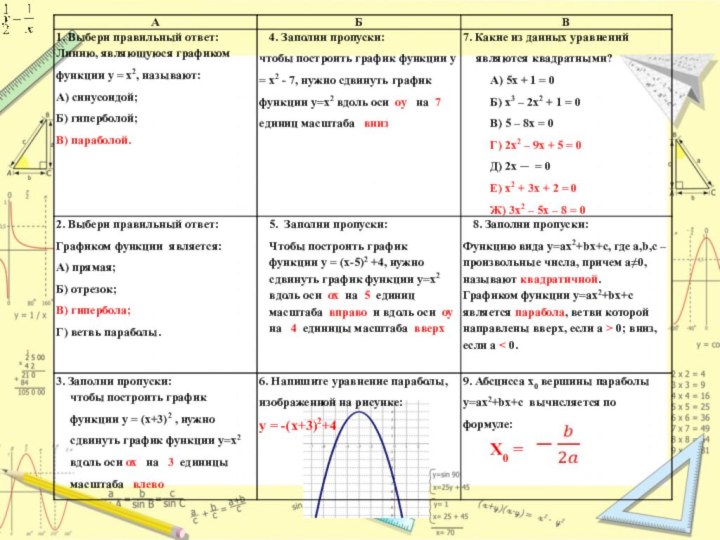
Цели урока:
1. Образовательные: познакомить учащихся с графическим способом
решения квадратных уравнений, повторить ранее изученные методы решения квадратных
уравнений, виды графиков и свойства функций у = х2, закрепить навыки построения графиков функций с помощью программ графопостроения Graphics, Plotter.2. Развивающие: развивать навыки творческой, познавательной, мыслительной деятельности, логическое мышление, вырабатывать умение анализировать и сравнивать.
3. Воспитательные: воспитывать сознательное отношение к учебному труду, развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие.
Слайд 9
Квадратное уравнение
(общий вид)
ax2 + bx + c=0
где а,
b, с-любые числа (коэффициенты),
причём а≠0.
Слайд 10 «Человеку, изучающему алгебру, часто полезнее решить одну и
ту же задачу различными способами, чем решать три-четыре различные
задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».У. У. Сойер.
Слайд 11
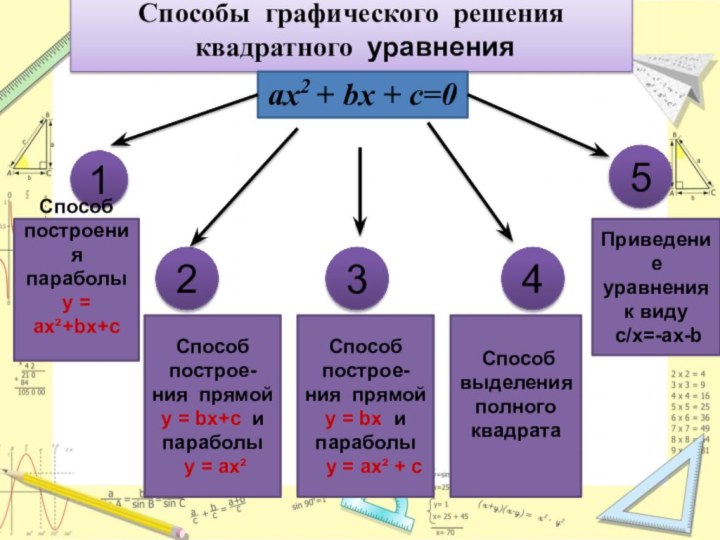
Способы графического решения
квадратного уравнения
ax2
+ bx + c=0
1
2
3
Способ построения параболы
y = ах²+bx+c
Приведение уравнения к виду
с/х=-ах-b
Способ поcтрое-
ния прямой
у = bx+c и параболы
у = ах²
Способ поcтрое-
ния прямой
у = bx и параболы
у = ах² + с
Способ выделения полного квадрата
4
5
Слайд 12
Алгоритм решения квадратного уравнения графическим способом
Построить график функции
y=ax2+bx+c (по алгоритму)
Найти точки пересечения графика с осью абсцисс
Выписать
абсциссы точек пересеченияСпособ 1
Слайд 13
3
-1
Построим график функции
х2-2х-3=0
1. График-парабола, а=1>0,ветви вверх.
2.
Вершина ( хₒ;уₒ) хₒ=-b/2a
хₒ=1
уₒ=1²-2·1-3=-4 (1;-4) – вершина3. Ось параболы хₒ=1
4. Дополнительные точки (0;-3), (2;-3)
Корнями уравнения являются абсциссы точек пересечения графика с осью х,
т.е. где у=0.
Значит, корни уравнения
-1 и 3.
Ответ: -1; 3.
Слайд 14
Алгоритм решения квадратного уравнения графическим способом
Способ 2
Преобразовать
уравнение к виду
ax2 = bx+с
Построить графики функции y
= ax2 и у = bx+ с
Найти абсциссы точек пересечения графиков.
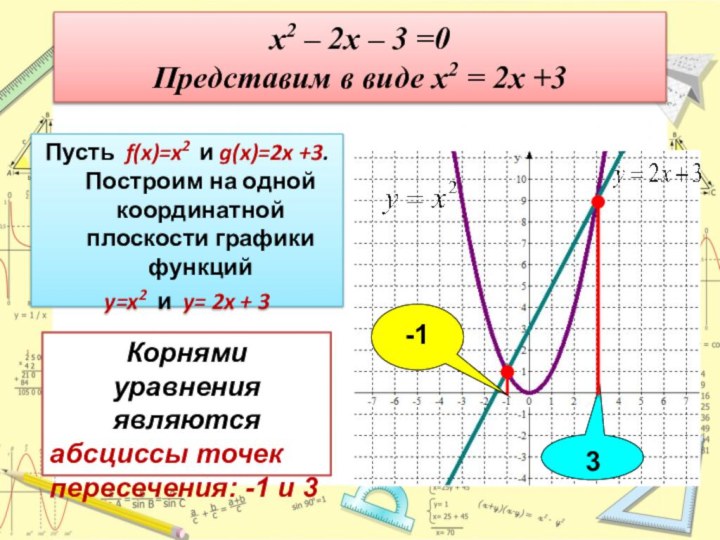
Слайд 15 x2 – 2x – 3 =0 Представим в
виде x2 = 2x +3
Пусть f(x)=x2 и g(x)=2x +3.
Построим на одной координатной плоскости графики функций y=x2 и y= 2x + 3
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
3
-1
Слайд 16
Алгоритм решения квадратного уравнения графическим способом
Способ 3
Преобразовать
уравнение к виду
ax2+с = bx
Построить:
параболу y
= ax2+с и прямую y = bxНайти абсциссы точек пересечения
графиков функции.
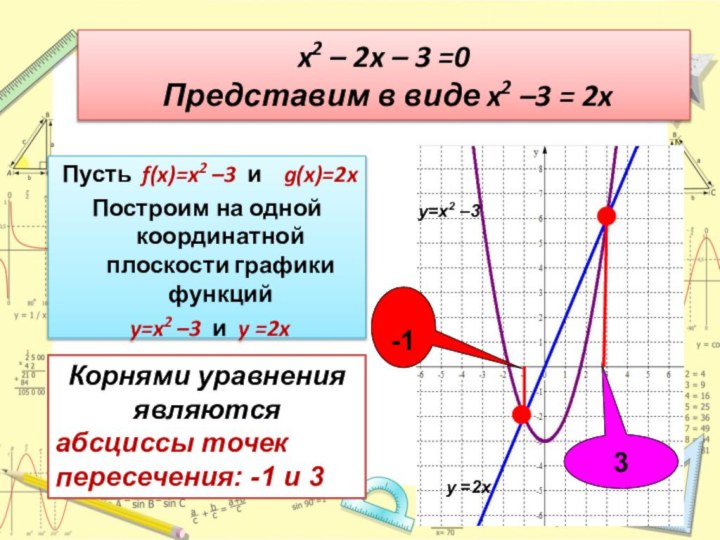
Слайд 17 x2 – 2x – 3 =0
Представим в виде x2
–3 = 2x Пусть f(x)=x2 –3 и g(x)=2x
Построим на одной координатной плоскости графики функций
y=x2 –3 и y =2x
-1
3
y=x2 –3
y =2x
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
Слайд 18
Преобразовать уравнение к виду
a(x + l)2 =
m
Построить:
параболу y = a(x + l)2 и
прямую y = mНайти абсциссы точек пересечения графиков функций.
Алгоритм решения квадратного уравнения графическим способом
Способ 4
(выделение полного квадрата)
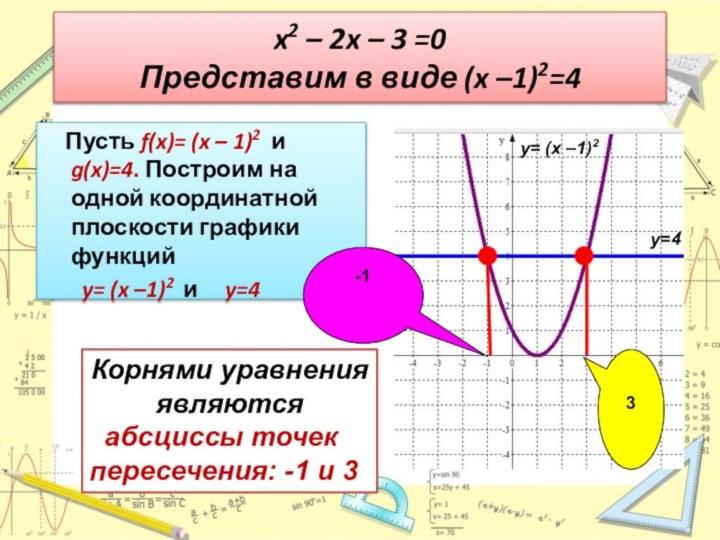
Слайд 19 x2 – 2x – 3 =0 Представим в
виде (x –1)2=4
Пусть f(x)= (x – 1)2
и g(x)=4. Построим на одной координатной плоскости графики функций y= (x –1)2 и y=4
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
3
-1
y= (x –1)2
y=4
Слайд 20
x2 – 2x = 3
Прибавим к левой части
равенства 1, чтобы получилась формула квадрата разности двух выражений:
х и 1; тогда и к правой части прибавим 1, получим:x2 – 2x + 1 = 3 + 1
Свернув формулу в левой части, получим:
( x –1)2=4
Выделение квадрата двучлена.
Слайд 21
Преобразовать уравнение к виду
с/х = - ax
- b
Построить графики функции
y =
- ax - b и у = с/хНайти абсциссы точек пересечения графиков.
Алгоритм решения квадратного уравнения графическим способом
Способ 5
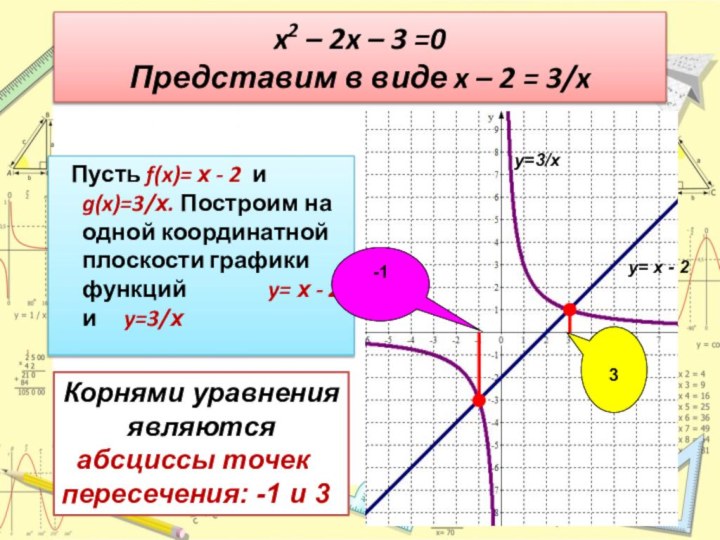
Слайд 22 x2 – 2x – 3 =0 Представим в
виде x – 2 = 3/x
Пусть f(x)=
х - 2 и g(x)=3/х. Построим на одной координатной плоскости графики функций y= х - 2 и y=3/хКорнями уравнения являются
абсциссы точек пересечения: -1 и 3
-1
3
y= х - 2
y=3/х





























