Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике Решение квадратных уравнений

Содержание

О создателях
«Решение квадратных уравнений»ВпередТема урока О создателях Определение:Квадратным уравнением называют уравнения вида аx2+bх+с=0, где а , b, с– Определение:Корнем квадратного уравнения аx2+bх+с=0 называют всякое значение переменной x, при котором квадратный Различные способы решения квадратного уравненияСпособ №1: Рассмотрим квадратный трехчлен x2-4х+3и разложим его Способ №2: Рассмотрим квадратный трехчлен x2-4х+3и разложим его на множители, используя метод Итак, мы решили уравнение двумя способами. Тем не менее знание этих способов Формулы корней квадратных уравнений Пусть дано квадратное уравнение аx2+bх+с=0. Преобразуем егоax2+bx+c=a(x2+(b/a)x)+c=a(x+b/2a)2-(b2-4ac)/4a. Теорема №1: Если D Теорема №2: Если D=0, то квадратное уравнение аx2+bх+с=0 имеет один корень, который Теорема №3: Если D>0, то квадратное уравнение аx2+bх+с=0 имеет два корня, которые Правило решения уравненияаx2+bх+с=01. Вычислить дискриминант по формуле D=b2-4ac.2. СамоконтрольДавайте проверим ваши знания по теме «Решение квадратных уравнений» Какое из следующих уравнений будет квадратным?5х+9=0-5х+2,5=58x2+4,5х+2=01/х+12=0 Разделить разность его корней на произведение коэффициентов;Найти все его корни или установить, Если дискриминант квадратного уравнения больше нуля, то…а) уравнение не имеет корней;б) Выбрать правильный ответ из предложенных вариантовУравнение x2-х-6=0 имеет 2 положительных корня.Уравнение Вы дали неправильный ответ Определение:Квадратным уравнением называют уравнения вида аx2+bх+с=0, где а , b, с– Определение:Корнем квадратного уравнения аx2+bх+с=0 называют всякое значение переменной x, при котором квадратный Правило решения уравненияаx2+bх+с=01. Вычислить дискриминант по формуле D=b2-4ac.2.
Слайды презентации

Слайд 2 О создателях

О создателях

Слайд 3 Определение:
Квадратным уравнением называют уравнения вида аx2+bх+с=0, где а

Определение:Квадратным уравнением называют уравнения вида аx2+bх+с=0, где а , b, с–

, b, с– любые действительные числа, причем а≠0.

Текст, выделенный

рамочкой, подлежит записи в тетрадь

Например:
5х2+3х-8=0
-3х2+8=0
2х2+11х=0

Слайд 4 Определение:
Корнем квадратного уравнения аx2+bх+с=0 называют всякое значение переменной

Определение:Корнем квадратного уравнения аx2+bх+с=0 называют всякое значение переменной x, при котором

x, при котором квадратный трехчлен аx2+bx+c обращается в нуль;

такое значение переменной х называют также корнем квадратного трехчлена.

Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.

Слайд 5 Различные способы решения квадратного уравнения

Способ №1: Рассмотрим квадратный

Различные способы решения квадратного уравненияСпособ №1: Рассмотрим квадратный трехчлен x2-4х+3и разложим

трехчлен x2-4х+3
и разложим его на множители, используя способ группировки.

Имеем
x2-4х+3= x2-x-3х+3=(х2-x)-(3x-3)=x(x-1)-3(x-1)=(x-1)(x-3).
Значит, заданное уравнение можно переписать в виде
(х-1)(х-3)=0, откуда ясно ,что уравнение имеет два корня;
х1=1, х2=3

Слайд 6 Способ №2: Рассмотрим квадратный трехчлен x2-4х+3
и разложим его

Способ №2: Рассмотрим квадратный трехчлен x2-4х+3и разложим его на множители, используя

на множители, используя метод выделения полного
квадрата.
Имеем


x2-4х+3= x2-4х+4-1=(х-2)2-1.
Воспользовавшись формулой разности квадратов, получим
(х-2-1)(х-2+1)=(х-1)(х-3).
Значит, заданное уравнение можно переписать в виде
(х-1)(х-3)=0, откуда ясно ,что уравнение имеет два корня;
х1=1, х2=3

Слайд 7 Итак, мы решили уравнение двумя способами. Тем не

Итак, мы решили уравнение двумя способами. Тем не менее знание этих

менее знание этих способов не есть панацея от всех

бед. Ведь наши успехи в решении квадратных уравнений зависели от одного благоприятного обстоятельства: квадратный трехчлен удавалось разложить на множители.
Математики нашли универсальный способ решения любых квадратных уравнений.

Слайд 8 Формулы корней квадратных уравнений
Пусть дано квадратное

Формулы корней квадратных уравнений Пусть дано квадратное уравнение аx2+bх+с=0. Преобразуем егоax2+bx+c=a(x2+(b/a)x)+c=a(x+b/2a)2-(b2-4ac)/4a.

уравнение аx2+bх+с=0. Преобразуем его
ax2+bx+c=a(x2+(b/a)x)+c=a(x+b/2a)2-(b2-4ac)/4a.
Обычно выражение b2-4ac обозначают буквой

D и называют дискриминантом квадратного уравнения аx2+bх+с=0.
Значит, квадратное уравнение аx2+bх+с=0 можно переписать в виде (x+(b/2a))2=D/4a2

Слайд 9 Теорема №1: Если D

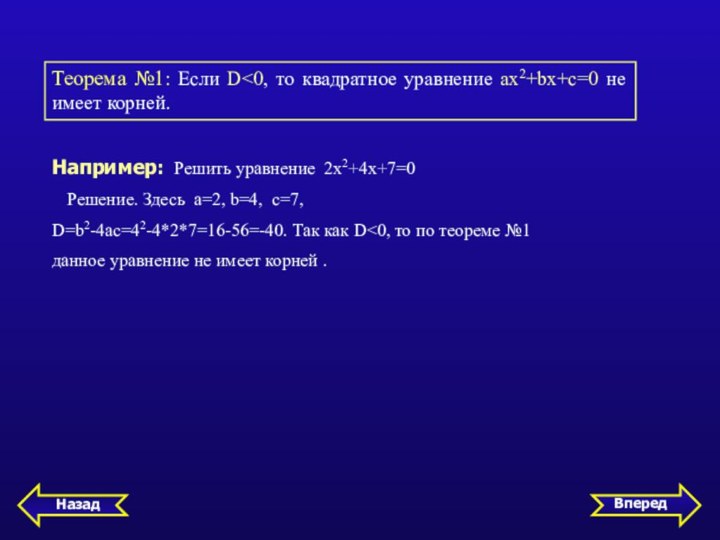
Теорема №1: Если D

не имеет корней.
Например: Решить уравнение 2х2+4х+7=0
Решение.

Здесь а=2, b=4, c=7,
D=b2-4ac=42-4*2*7=16-56=-40. Так как D<0, то по теореме №1
данное уравнение не имеет корней .

Слайд 10 Теорема №2: Если D=0, то квадратное уравнение аx2+bх+с=0

Теорема №2: Если D=0, то квадратное уравнение аx2+bх+с=0 имеет один корень,

имеет один корень, который находится по формуле х=-b/2a.
Например:

Решить уравнение х2-2х+1=0
Решение. Здесь а=1, b=-2, c=1,
D=b2-4ac=(-2)2-4*1*1=4-4=0. Так как D=0, то по теореме №2
данное уравнение имеет корень х=-b/2a=2/2=1 .

Слайд 11 Теорема №3: Если D>0, то квадратное уравнение аx2+bх+с=0

Теорема №3: Если D>0, то квадратное уравнение аx2+bх+с=0 имеет два корня,

имеет два корня, которые находится по формулам
х1=(-b+√D)/2a, х2=(-b-√D)/2a
Например:

Решить уравнение 3х2+8х-11=0
Решение. Здесь а=3, b=8, c=-11,
D=b2-4ac=(8)2-4*3*(-11)=64+132=196. Так как D>0, то по теореме №3
данное уравнение имеет 2 корня:
х1=(-b+√D)/2a=(-8+14)/6=1; х2=(-b-√D)/2a=(-8-14)/6=-11/3

Слайд 12 Правило решения уравнения
аx2+bх+с=0
1. Вычислить дискриминант по формуле

Правило решения уравненияаx2+bх+с=01. Вычислить дискриминант по формуле D=b2-4ac.2. Если D0,

D=b2-4ac.
2. Если D

не имеет корней.
3. Если D=0, то квадратное уравнение имеет один корень: x = - b/2a
Если D>0, то квадратное уравнение имеет два корня:
x1=(-b+√D)/2a; х2=(-b-√D)/2a.

Слайд 13

Слайд 14 Самоконтроль
Давайте проверим ваши знания по теме
«Решение квадратных

СамоконтрольДавайте проверим ваши знания по теме «Решение квадратных уравнений»

уравнений»

Слайд 15 Какое из следующих уравнений будет квадратным?
5х+9=0
-5х+2,5=5
8x2+4,5х+2=0
1/х+12=0

Какое из следующих уравнений будет квадратным?5х+9=0-5х+2,5=58x2+4,5х+2=01/х+12=0

Слайд 16 Разделить разность его корней на произведение коэффициентов;
Найти все

Разделить разность его корней на произведение коэффициентов;Найти все его корни или

его корни или установить, что корней нет;
Сложить все коэффициенты

уравнения;

Доказать что корней нет;

Что значит решить квадратное уравнение?

Слайд 17 Если дискриминант квадратного уравнения больше нуля, то…
а)

Если дискриминант квадратного уравнения больше нуля, то…а) уравнение не имеет

уравнение не имеет корней;
б) уравнение имеет один корень;
в) про

уравнение ничего сказать нельзя;

г) уравнение имеет 2 корня;

Слайд 18 Выбрать правильный ответ из предложенных вариантов
Уравнение x2-х-6=0

Выбрать правильный ответ из предложенных вариантовУравнение x2-х-6=0 имеет 2 положительных

имеет 2 положительных корня.
Уравнение x2+2х+3=0 не имеет корней.
Уравнение 3x2+7х-6=0

имеет один корень.

Уравнение x2-3х+2=0 имеет 2 отрицательных корня.

Слайд 19
Вы дали неправильный ответ

Вы дали неправильный ответ

Слайд 20 Определение:
Квадратным уравнением называют уравнения вида аx2+bх+с=0, где а

Определение:Квадратным уравнением называют уравнения вида аx2+bх+с=0, где а , b, с– любые действительные числа, причем а≠0Например:5х2+3х-8=0-3х2+8=02х2+11х=0

, b, с– любые действительные числа, причем а≠0
Например:
5х2+3х-8=0
-3х2+8=0
2х2+11х=0

Слайд 21 Определение:
Корнем квадратного уравнения аx2+bх+с=0 называют всякое значение переменной

Определение:Корнем квадратного уравнения аx2+bх+с=0 называют всякое значение переменной x, при котором

x, при котором квадратный трехчлен аx2+bx+c обращается в нуль;

такое значение переменной х называют также корнем квадратного трехчлена.

Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.

  • Имя файла: prezentatsiya-po-matematike-reshenie-kvadratnyh-uravneniy.pptx
  • Количество просмотров: 158
  • Количество скачиваний: 0
- Предыдущая Гиподинамия
Следующая - Презентация по физике Путешествие в страну физических приборов

Похожие презентации

Презентация по математике координатная прямая ... Презентация по математике координатная прямая ... 142
Презентация по математике на тему Первообразная  (11 класс) Презентация по математике на тему Первообразная  (11 класс) 132
Координатная плоскость с координатами Координатная плоскость с координатами 153
Линейная функция Линейная функция 176
Презентация к уроку алгебра 9классПреобразование графиков функций Презентация к уроку алгебра 9классПреобразование графиков функций 174
Урок по математике на тему История математики 8 класс Урок по математике на тему История математики 8 класс 176
Алгебраические кривые в полярной системе координат и их применение в природе и технике Алгебраические кривые в полярной системе координат и их применение в природе и технике 157
Решение кубических уравнений Решение кубических уравнений 233
Действительные числа Действительные числа 149
Степень с целым показателем Степень с целым показателем 122
Презентация к мероприятию Математическая викторина Презентация к мероприятию Математическая викторина 166
Презентация по алгебре по теме Решение тригонометрических уравнений Презентация по алгебре по теме Решение тригонометрических уравнений 207
Внеклассное мероприятие на тему: Любовь с первого взгляда к математике Внеклассное мероприятие на тему: Любовь с первого взгляда к математике 193
Анализ геометрических высказываний - 11 Анализ геометрических высказываний - 11 144
Урок по теме Рациональные выражения Урок по теме Рациональные выражения 168
КВАДРАТНЫЙ КОРЕНЬ КВАДРАТНЫЙ КОРЕНЬ 143
Метод математической индукции Метод математической индукции 159
Тренажёр Решу ВПР: простейшие логические задачи, часть 4 Тренажёр Решу ВПР: простейшие логические задачи, часть 4 191
Задачи на дроби Задачи на дроби 167
Решение задач с помощью рациональных уравнений Решение задач с помощью рациональных уравнений 154
Презентация к уроку математики в 11 классе на тему Иррациональные уравнения Презентация к уроку математики в 11 классе на тему Иррациональные уравнения 169
Конспект и презентация к уроку по теме Линейная функция Конспект и презентация к уроку по теме Линейная функция 151
Показательная функция, её свойства и график Показательная функция, её свойства и график 178
Логарифмы Логарифмы 127
Чётность и нечётность функции Чётность и нечётность функции 136
Задачи и упражнения на готовых чертежах Определение и признак параллелограмма Задачи и упражнения на готовых чертежах Определение и признак параллелограмма 215
Презентация к уроку Тригонометрические функции Презентация к уроку Тригонометрические функции 66
Графики линейного уравнения с двумя переменными Графики линейного уравнения с двумя переменными 163
Сложение и вычитание многочленов Сложение и вычитание многочленов 143
Графики функций с модулями Графики функций с модулями 161