- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Прогрессии 9 класс
Содержание
- 2. СодержаниеЧисловая последовательностьАрифметическая
- 3. Числовая последовательностьФункцию y=f(x), определённую на множестве натуральных
- 4. Числовая последовательностьСпособы задания последовательности:Аналитический (указывается формула n-го
- 5. Числовая последовательностьРешаем:№1. Известно, что(аn)-возрастающая последовательность кубов всех
- 6. Числовая последовательность№3. По заданной формуле n-го члена
- 7. Числовая последовательность№4. Выпишите первые шесть членов последовательности
- 8. Получилось? МОЛОДЕЦ!!!
- 9. Арифметическая прогрессияОпределение. Арифметическая прогрессия – это числовая
- 10. Арифметическая прогрессияЕсли d>0 — арифметическую прогрессию называют возрастающей; Если d
- 11. Основные формулы
- 12. Арифметическая прогрессияХарактеристическое свойство арифметической
- 13. РешаемВ арифметической прогрессии, первый член которой равен
- 14. Решаем(аn) – арифметическая прогрессияа10 = 8, а12
- 15. РешаемПятый член арифметической прогрессии на 15 меньше
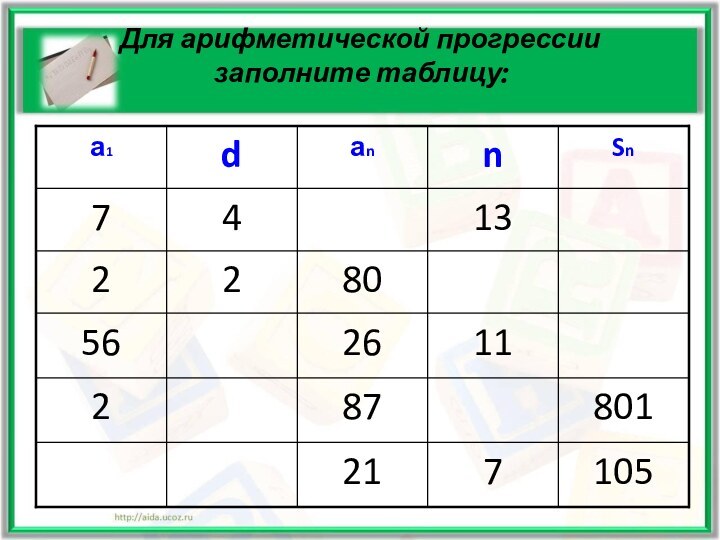
- 16. Для арифметической прогрессии заполните таблицу:
- 17. Проверим ответыаn = 55; Sn =
- 18. РешаемВычислите сумму:50² – 49² + 48² –
- 19. Решить самостоятельноНайдите семнадцатый член арифметической прогрессии (a):
- 20. Получилось? МОЛОДЕЦ!!!
- 21. Геометрическая прогрессия
- 22. Это интересноКакие явления в природе напоминают геометрическую прогрессию?
- 23. КАК БЫСТРО РАЗМНОЖАЕТСЯ ВСЕМ ИЗВЕСТНАЯ КОМНАТНАЯ МУХА?ПУСТЬ
- 24. •15 АПРЕЛЯ - САМКА ОТЛОЖИЛА 120 ЯИЦ;
- 25. •5 июля - 12960000 самок кладут по
- 26. Чтобы яснее представить себе эту огромную массу
- 27. По определению геометрической прогрессии:Формула n-го члена
- 28. Основные
- 29. Геометрическая прогрессия4)
- 30. ЗапомниХорошо освоив формулы, можно научиться с легкостью решать задачи с арифметической и геометрической прогрессиями.
- 31. Геометрическая прогрессияРешаем:Решение:
- 32. Решаем
- 33. РешаемНайдем, например,сумму первых восьмичленов геометрическойпрогрессии ( bn),
- 34. Решить самостоятельно 1 вариантДана геометрическая прогрессияb1=-4, q=2.
- 35. Проверь себя1 вариантS5 =2)2 вариантS6 =2)S6 =S5 =
- 36. Математический диктант 1. Запишите формулу, по которой
- 37. Математический диктант (продолжение)6. Найдите первый член арифметической
- 38. Ответы к математическому диктантуа25 =а24 + dв7
- 39. Получилось?МОЛОДЕЦ!!!
- 40. Интересные факты:1) Химия. При повышении температуры по
- 41. Интересные факты:4) Биология. Микроорганизмы размножаются делением пополам,
- 42. Проектная работаСоставить две задачи
- 43. Скачать презентацию
- 44. Похожие презентации
СодержаниеЧисловая последовательностьАрифметическая прогрессияГеометрическая прогрессия










































Слайд 3
Числовая последовательность
Функцию y=f(x), определённую на множестве натуральных чисел
х ЄN (или его конечном подмножестве), называют числовой последовательностью
и обозначают y=f(n),или у1, у2,… , уn, …, или (уn).
Виды числовой последовательности:
конечная
бесконечная
Слайд 4
Числовая последовательность
Способы задания последовательности:
Аналитический (указывается формула n-го члена
последовательности).
Словесный (правило составления последовательности выражается словесным описанием).
Рекурентный (указывается правило
позволяющее вычислить n-й член данной последовательности, если известны все её предыдущие члены).
Слайд 5
Числовая последовательность
Решаем:
№1. Известно, что(аn)-возрастающая последовательность кубов всех натуральных
чисел.
Назовите а1;а2;а3;а4.
№2. Известно, (с n)-возрастающая последовательность
всех натуральных степеней числа 2.Назовите с1;с2;с3;с4;с5
Слайд 6
Числовая последовательность
№3. По заданной формуле n-го члена последовательности
вычислите первые пять членов последовательности:
а) аn =
4n +1 б) сn=-7n+3в) вn=-2/3- n г) хn= n² +1
Слайд 7
Числовая последовательность
№4. Выпишите первые шесть членов последовательности (хn),
заданной рекуррентно:
а) х1=1; хn= -хn-1+5 (n =
2;3;4;…)б) х1=-5; хn= хn-1+10 (n = 2;3;4;…)
в) х1=-512; хn= 0,5хn-1 (n = 2;3;4;…)
Слайд 9
Арифметическая прогрессия
Определение. Арифметическая прогрессия – это числовая последовательность,
где каждый последующий член равен предыдущему, сложенным с одним
и тем же числом d.Число d называется разностью арифметической прогрессии.
Слайд 10
Арифметическая прогрессия
Если d>0 — арифметическую прогрессию
называют возрастающей;
Если d
все члены прогрессии равны числу a, то арифметическую прогрессию называют стационарной.Слайд 11 Основные формулы арифметической
прогрессии
1) формула n-го члена прогрессии
2) формула СУММЫ n-первых
членов прогрессии 3) свойство арифметической прогрессии
Слайд 12
Арифметическая прогрессия
Характеристическое свойство арифметической прогрессии
:
Числовая последовательность является арифметической прогрессией тогда и только тогда,
когда каждый ее член, кроме первого (и последнего, в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.
Слайд 13
Решаем
В арифметической прогрессии, первый член которой равен -3,4,
а разность равна 3, найдите пятый и одиннадцатый члены.
Решение:
Для нахождения n-ого члена арифметической прогрессии воспользуемся формулой:
an = a1 + (n-1)d.
Имеем:
a5 = a1 + (5 – 1)d = -3,4 + 4 · 3 = 8,6;
a11 = a1 + (11 – 1)d = -3,4 + 10 · 3 = 26,6.
Ответ: 8,6 и 26,6
Слайд 14
Решаем
(аn) – арифметическая прогрессия
а10 = 8, а12 =
-2. Найдите а11.
Решение:
Согласно характеристическому свойству арифметической
прогрессии:аn= (аn+1+ аn-1)/2;
Имеем а11 = (8 – 2)/2=3
Ответ: а11= 3
Слайд 15
Решаем
Пятый член арифметической прогрессии на 15 меньше второго.
Сумма третьего и седьмого её членов равна -6.
Найдите третий и четвёртый члены этой прогрессии.Решение: составим систему уравнений
а2-а5=15,
а3+а7=-6;
а1+ d - (а1+ 4d)=15,
(а1+2d) + (а1+6d) =-6;
d=-5,
а1=17;
Итак: а3 = а1+2d, т.е. а3=7,
а4 = а3+d, а4=2.
Ответ: а3=7, а4=2.
Слайд 17
Проверим ответы
аn = 55; Sn = 403
n
= 40; Sn = 1640
d = -3;
Sn = 451d = 5; n = 18
а1 = 9; d= 2
Слайд 18
Решаем
Вычислите сумму:
50² – 49² + 48² – 47²
+ 46² – 45² +…
… + 4² –
3² +2² – 1²Решение:
Воспользуйтесь формулой разности квадратов: (50-49)(50+49) + (48-47)(48+47) + (46-45)(46+45) +…+ (4-3)(4+3) + (2-1)(2+1)
2) Выполните действия в скобках:
99 + 95 + 91 + 87 +… + 7 + 3; эти числа образуют убывающую арифметическую прогрессию a1=99, an=3, n=25.
Ответ: сумма равна 1275.
Слайд 19
Решить самостоятельно
Найдите семнадцатый член арифметической прогрессии (a):
-18; -15; -12;… .
Найдите сумму
первых двадцати членов этой прогрессии (a): -18; -15; -12;… .
Найдите разность арифметической прогрессии (a), если:
a=-28, a=16.
Ответы: 1) 30 2) 210 3) -4
Слайд 21
Геометрическая прогрессия
ОПРЕДЕЛЕНИЕ:
Геометрической прогрессией называется числовая последовательность отличных от нуля чисел,
каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число (q).Число q называется знаменателем геометрической прогрессии.
Если q<1, то геометрическая прогрессия называется бесконечно убывающей
Слайд 23
КАК БЫСТРО РАЗМНОЖАЕТСЯ ВСЕМ ИЗВЕСТНАЯ КОМНАТНАЯ МУХА?
ПУСТЬ КАЖДАЯ
МУХА ОТКЛАДЫВАЕТ 120 ЯИЧЕК И ПУСТЬ В ТЕЧЕНИЕ ЛЕТА
УСПЕВАЕТ ПОЯВИТЬСЯ 7 ПОКОЛЕНИЙ МУХ, ПОЛОВИНА КОТОРЫХ - САМКИ. ЗА НАЧАЛО ПЕРВОЙ КЛАДКИ ПРИМЕМ 15 АПРЕЛЯ И БУДЕМ СЧИТАТЬ, ЧТО МУХА-САМКА В 20 ДНЕЙ ВЫРАСТАЕТ НАСТОЛЬКО, ЧТО САМА ОТКЛАДЫВАЕТ ЯЙЦА. ТОГДА РАЗМНОЖЕНИЕ БУДЕТ ПРОИСХОДИТЬ ТАК:Слайд 24 •15 АПРЕЛЯ - САМКА ОТЛОЖИЛА 120 ЯИЦ; В
НАЧАЛЕ МАЯ - ВЫШЛО 120 МУХ, ИЗ НИХ 60
САМОК. •5 МАЯ - КАЖДАЯ САМКА КЛАДЕТ 120 ЯИЦ; В СЕРЕДИНЕ МАЯ - ВЫХОДИТ 60 X 120 = 7200 МУХ, ИЗ НИХ 3600 САМОК; •25 МАЯ - КАЖДАЯ ИЗ 3600 САМОК КЛАДЕТ ПО 120 ЯИЦ; В НАЧАЛЕ ИЮНЯ - ВЫХОДИТ 3600 X 120 = 432 000 МУХ, ИЗ НИХ 216000 САМОК; •14 ИЮНЯ - КАЖДАЯ ИЗ 216000 САМОК КЛАДЕТ ПО 120 ЯИЦ; В КОНЦЕ ИЮНЯ - ВЫХОДИТ 25920000 МУХ, В ИХ ЧИСЛЕ 1296000 САМОК;Слайд 25 •5 июля - 12960000 самок кладут по 120
яиц; в июле - выходит 1555200000 мух, среди них
777600000 самок;•25 июля - выходит 93312000000 мух, среди них 46656000000 самок;
•13 августа - выходит 5598720000000 мух, среди них 2799360000000 самок;
•1 сентября - выходит 355923200000000 мух.
Слайд 26 Чтобы яснее представить себе эту огромную массу мух,
которые при беспрепятственном размножении могли бы в течение одного
лета народиться от одной пары, вообразим, что они выстроены в прямую линию, одна около другой. Так как длина мухи 5 мм, то все эти мухи вытянулись бы на 2500 млн. км - в 18 раз больше, чем расстояние от Земли до Солнца (т. е. примерно, как от Земли до далекой планеты Уран)...Слайд 28 Основные формулы
геометрической
прогрессииформула n-го члена прогрессии .
2) формула суммы n-первых членов прогрессии
3) Свойство геометрической прогрессии
Слайд 30
Запомни
Хорошо освоив формулы, можно научиться с легкостью решать
задачи с арифметической и геометрической прогрессиями.
Слайд 33
Решаем
Найдем, например,
сумму первых восьми
членов геометрической
прогрессии ( bn), в
которой
b1 = 3 ; q = -2.
Решение:
S8 = b1(q8
– 1 )/(q – 1) = 3 •((-2)8 – 1)/(-2 – 1) = =3· 255/(-3) = -255Ответ: S8 = -255
Слайд 34
Решить самостоятельно
1 вариант
Дана геометрическая прогрессия
b1=-4, q=2. Найти S5
b1=4, b2=16. Найти S6
2 вариант
Дана геометрическая прогрессия
b1=-9, q=2. Найти
S6b1=3, b2=9. Найти S5
Слайд 36
Математический диктант
1. Запишите формулу, по которой можно найти
неизвестный 25-й член арифметической прогрессии, если известен предыдущий член
и разность.2. Вычислите 7-й член геометрической прогрессии, если известно, что 6-й член равен 50, а знаменатель 0,1.
3. Запишите формулу по которой можно вычислить 37-й член геометрической прогрессии, если вам известен первый член и знаменатель.
4. Запишите формулу, по которой можно найти неизвестный 16-й член арифметической прогрессии, если известен первый член и разность.
5. Вычислите 6-й член геометрической прогрессии, если ее первый член 3, а знаменатель равен 2.
Слайд 37
Математический диктант
(продолжение)
6. Найдите первый член арифметической прогрессии, если
ее десятый член равен 5, а разность 4.
7. Запишите
формулу для нахождения первого члена геометрической прогрессии, если известен п-й член и знаменатель.8. Выразите разность арифметической прогрессии из рекуррентного правила.
9. Выразите разность из формулы п-го члена арифметической прогрессии.
10. Выразите знаменатель геометрической прогрессии из рекуррентного правила.
11. Выразите знаменатель из формулы п-го члена геометрической прогрессии.
Слайд 38
Ответы к математическому диктанту
а25 =а24 + d
в7 =
в6 · q⁶ = 50 · 0,1⁶ =
в37=
в1· q³⁶а16 =а1 + d·15
в6 =в1 · q⁵ = 3·2⁵ = 96
а10 = а1 + d·9 ;
а1= а10 - d·9 =5-4·9=-31
вn= в1 · qⁿ⁻¹ ;
в1 = вn : qⁿ⁻¹
8. d = аn+1 - аn
аn = а1 + d(n-1);
d=(аn –а1): (n-1)
10. q = вn+1 : вn
вn= в1 · qⁿ⁻¹; qⁿ⁻¹= вn: в1;
Критерии оценок:
5 - 6 правильно выполненных заданий выставляется отметка «3»;
7 – 8 заданий выставляется отметка «4»;
9 -10 заданий выставляется отметка «5».
Слайд 40
Интересные факты:
1) Химия. При повышении температуры по арифметической
прогрессии скорость химических реакций растет по геометрической прогрессии.
2) Геометрия.
Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию. Какие величины в треугольнике образуют геометрическую прогрессию?
3) Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.
Слайд 41
Интересные факты:
4) Биология. Микроорганизмы размножаются делением пополам, поэтому
при благоприятных условиях, через одинаковый промежуток времени их число
удваивается.5) Экономика. Вклады в сбербанке ежегодно увеличиваются на одинаковый процент.
Вклад составляет 1000 рублей при 4% годовых. Какую сумму получит вкладчик через 3 года?