параболы;
Определение координат вершины параболы;
Определение оси симметрии.
Определение точек пересечения с
осями координат;Нахождение дополнительных точек.
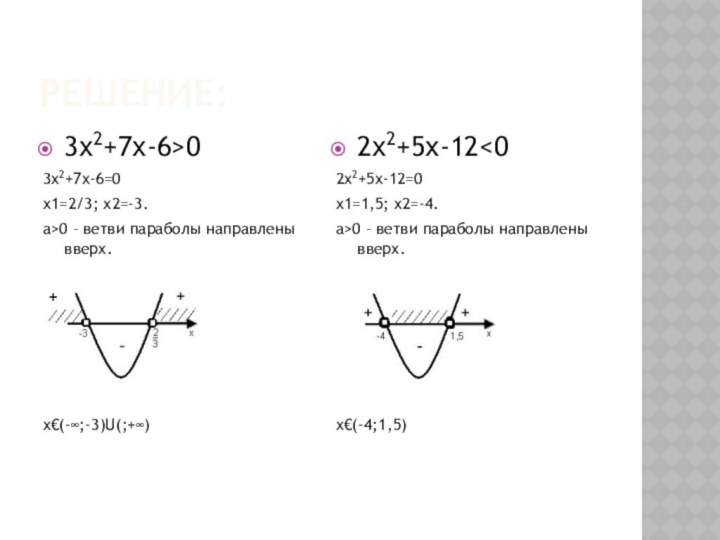
а>0 – ветви параболы направлены вверх.
х0=-в/2а, х0=3, у0=у(3)=-1.
х=3.
х2-6х+8=0, х1=2, х2=4; у(0)=8. Точки (2;0), (4;0), (0;8).
У(1)=3, у(5)=3.







![Презентация по алгебре на тему Решение квадратных неравенств (9 класс) РЕШИТЬ НЕРАВЕНСТВО: Х2+4Х-5≥0.Итог: Значения функции положительны и равны нулю (неотрицательны) при х€(-∞;-5]U[1;+∞).](/img/tmb/7/633051/0016b972d73ba389cc9e672fd57b9b62-720x.jpg)



![Презентация по алгебре на тему Решение квадратных неравенств (9 класс) Х2-6Х+8≤0Ответ: Х€[2;4].](/img/tmb/7/633051/b3a348d9583ba9b4b26a581c053d33c0-720x.jpg)


![Презентация по алгебре на тему Решение квадратных неравенств (9 класс) РЕШЕНИЕ: х2-3х-18≤0х2-3х-18=0х1+х2=3, х1∙х2=-18.х1=6, х2=-3.а>0 – ветви параболы направлены вверх.х€[-3;6]х2-2х-8≥0х2-2х-8=0х1+х2=2, х1∙х2=-8.х1=4, х2=-2.а>0 – ветви параболы направлены вверх.х€(-∞;-2]U[4;+∞)](/img/tmb/7/633051/4b0b493c98dcdf8d13c606ce8b533f83-720x.jpg)