Презентация на тему по математике на тему Решение тригонометрических неравенств

тему «Основы тригонометрии» отводится мало времени, а материал, изучаемый

в теме довольно объемный и сложный.
Тема «Тригонометрические неравенства» изучается только в ознакомительном порядке, но в варианты различного вида экзаменационных работ по математике она включается довольно часто.
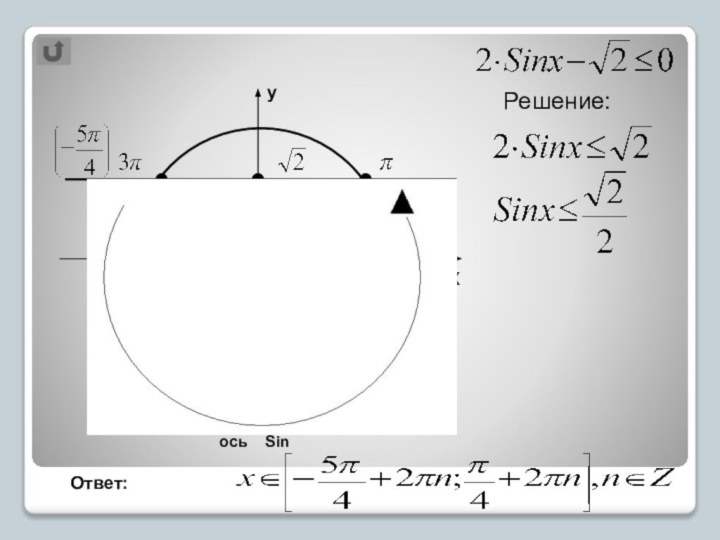
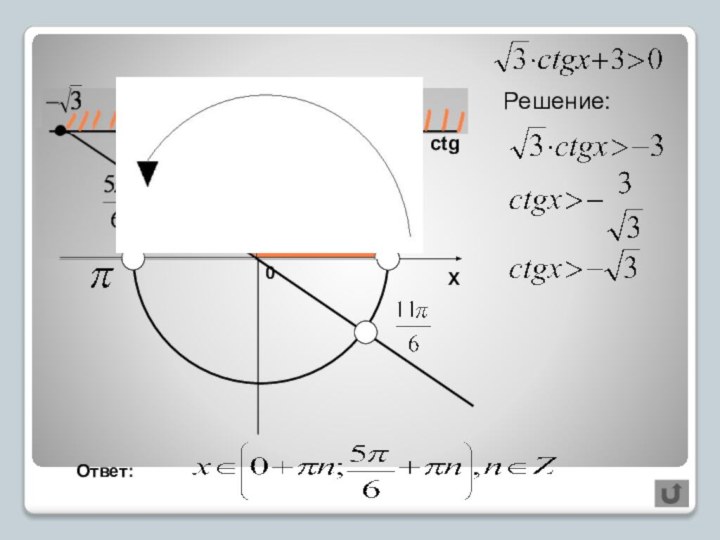
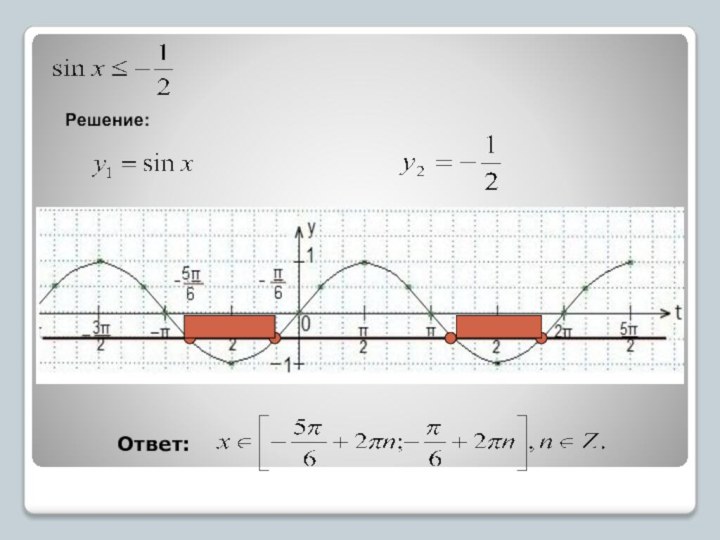
Знать алгоритмы решения и уметь решать простые тригонометрические неравенства необходимо.

различные способы решения простых тригонометрических неравенств;
составить наиболее простой алгоритм

решения тригонометрических неравенств;
научиться решать простые
тригонометрические неравенства.

какое из них больше и какое меньше, посредством одного

из знаков: < (меньше); > (больше); ≥ (больше или равно), < (меньше или равно).

Решить неравенство — это значит найти множество всех его решений.

Решением неравенства называются все значения переменной, при которых неравенство становится верным.

находится под знаком тригонометрической функции.

Простое тригонометрическое неравенство – неравенство,

в котором неизвестная переменная находится под знаком одной тригонометрической функции.

помощью числовой окружности;

Решение тригонометрических неравенств с помощью графика

функции.

Решение тригонометрических неравенств с

помощью числовой окружности

решение тригонометрических неравенств с синусом и косинусом;
решение тригонометрических неравенств с тангенсом и котангенсом.

все числа в правую часть неравенства;
Начертить единичную окружность и

отметить на ней ось sin или ось cos;
Отметить на оси число из правой части неравенства;
Через отмеченную точку провести прямую параллельную оси X или У;
Отметить точки пересечения прямой с окружностью, определить их значения;
Закрасить ту часть круга, которая является решением неравенства;
В закрашенной части указать стрелкой направление обхода окружности (против часовой стрелки);
Проверить, чтобы стрелка была направлена от меньшего угла к большему (если это не выполняется, то больший угол заменить соответствующим меньшим);
Записать ответ с учетом периода 2Пn.

 

Перенести все числа в правую часть неравенства;
2. Начертить единичную

окружность и отметить на ней ось tg или ctg;
3. Отметить на оси число из правой части неравенства;
4. Через отмеченное число и центр окружности провести прямую;
5. Отметить точки пересечения прямой с окружностью, определить их значение;
6. Отметить на окружности точки в которых tg и ctg не пределен;
7. Закрасить ту часть круга, которая является решением неравенства;
8. В закрашенной части указать направление обхода окружности (против часовой стрелки);
9. Проверить, чтобы стрелка была направлена от меньшего угла к большему (если это не выполняется, то больший угол заменить соответствующим меньшим);
10. Записать ответ с учетом периода Пn.

Перенести все числа в правую часть неравенства;
Выписать

функции входящие в неравенство;
Построить в одной системе координат графики этих функций;
Отметить на рисунке точки пересечения графиков функций;
Выделить части графиков, удовлетворяющие неравенству;
Записать ответ, учитывая период тригонометрической функции входящей в неравенство.

изучены виды, способы решения и алгоритмы решения простых тригонометрических

неравенств;
Составлены алгоритмы решения простых тригонометрических неравенств;
Рассмотрено решение тригонометрических неравенств с применением алгоритмов.