интеграл
Вычисление определенного интеграла
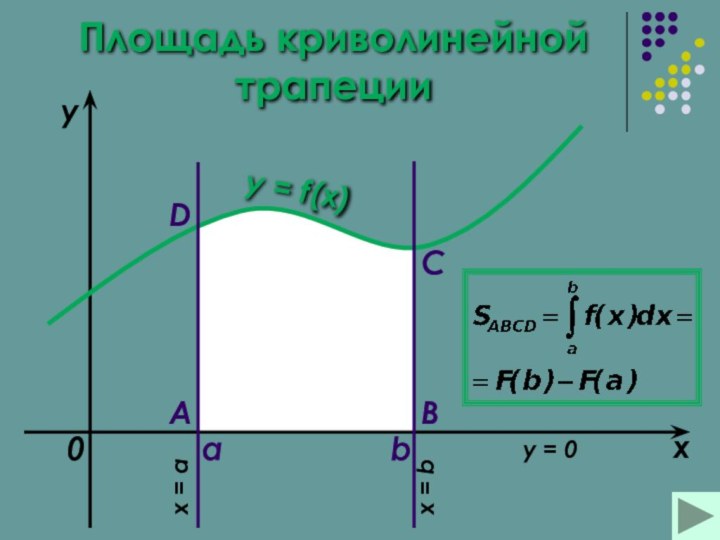
Площадь криволинейной трапеции
Площадь криволинейной
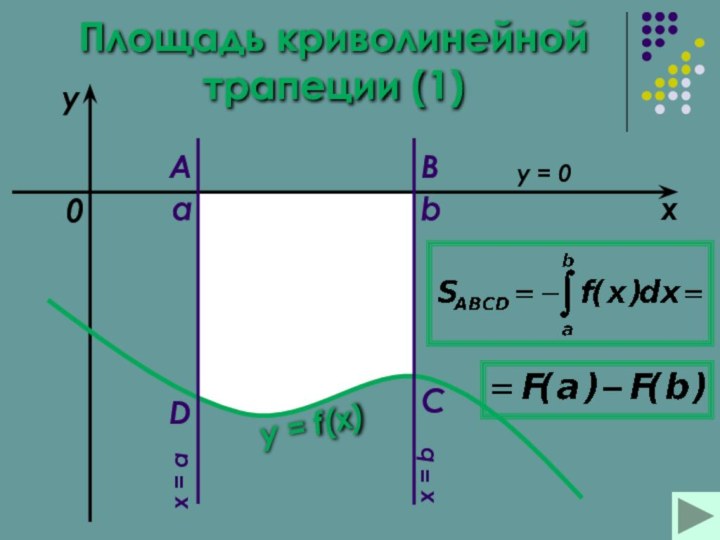
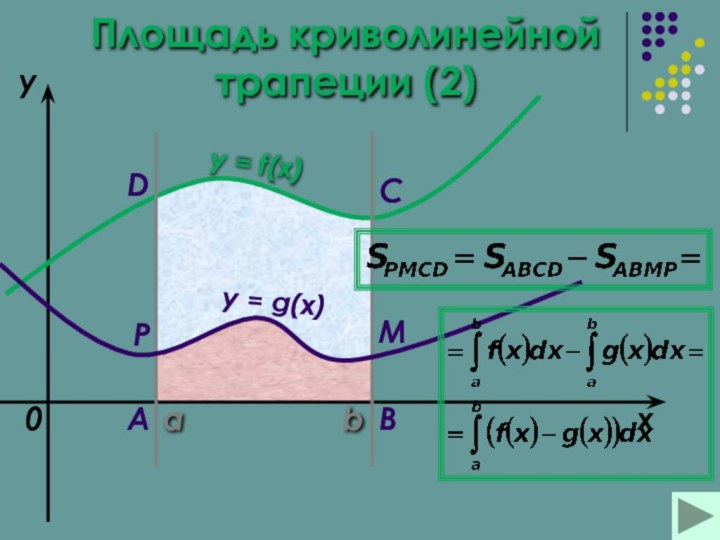
трапеции Площадь криволинейной трапеции (1)Площадь криволинейной трапеции Площадь криволинейной трапеции (2)
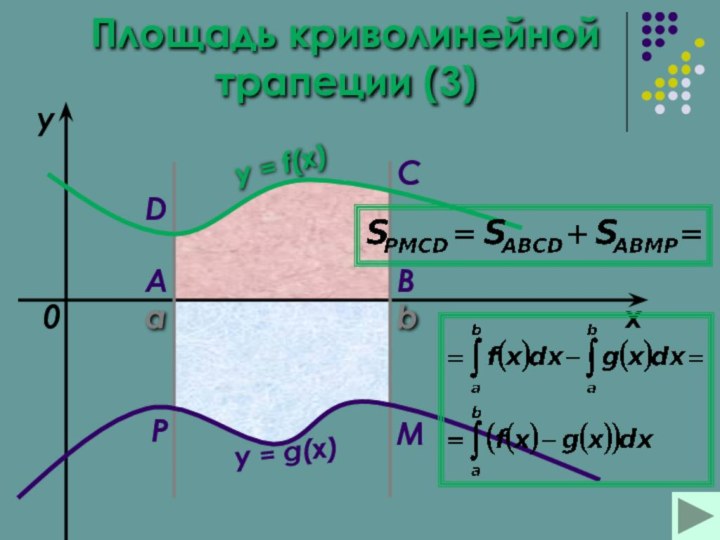
Площадь криволинейной трапеции Площадь криволинейной трапеции (3)
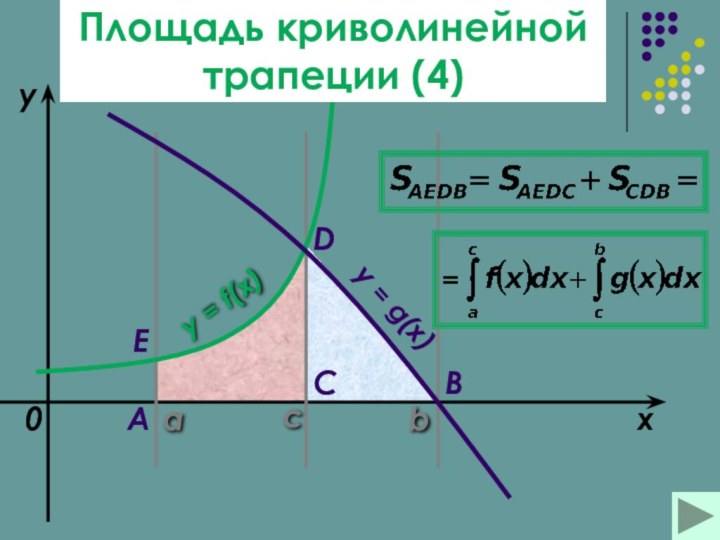
Площадь криволинейной трапецииПлощадь криволинейной трапеции (Площадь криволинейной трапеции (4Площадь криволинейной трапеции (4)
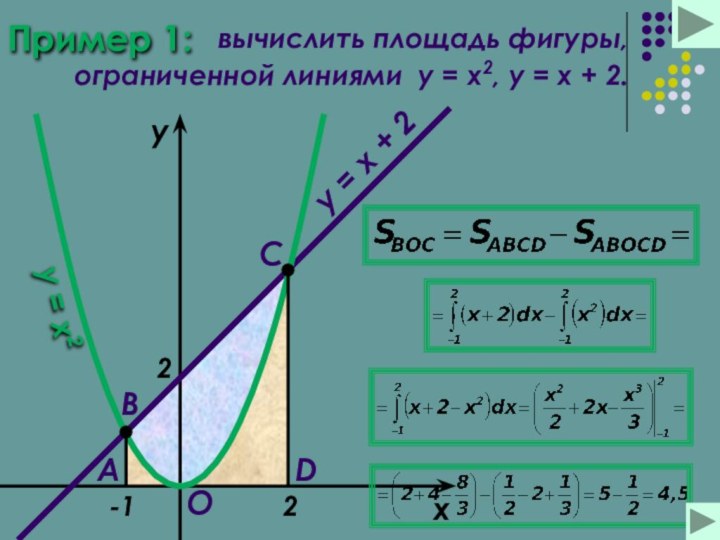
Пример (1)
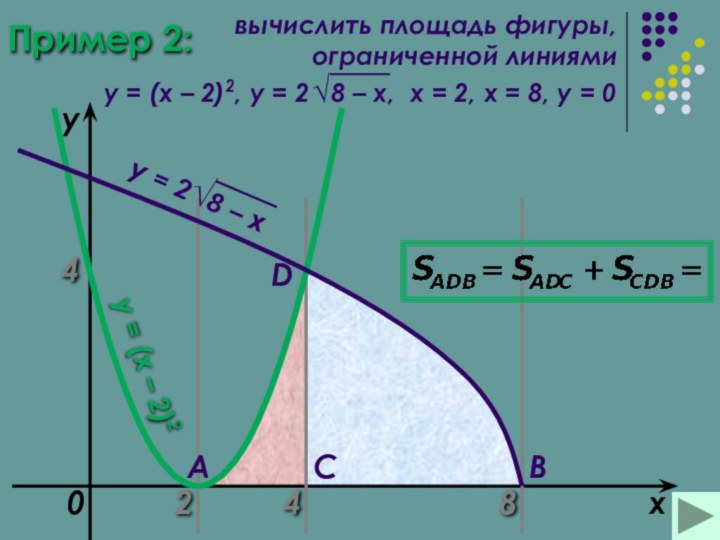
Пример (2)