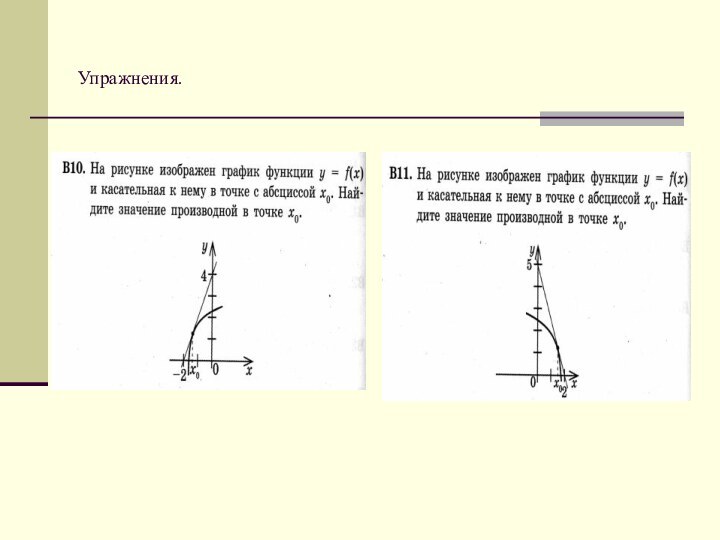
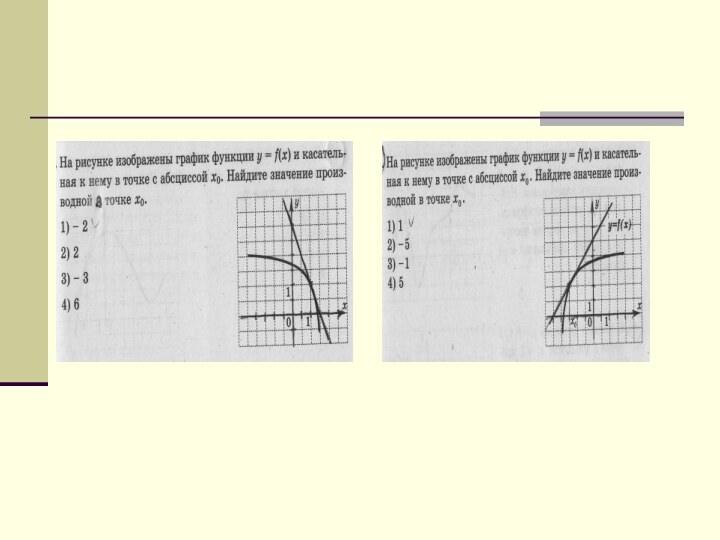
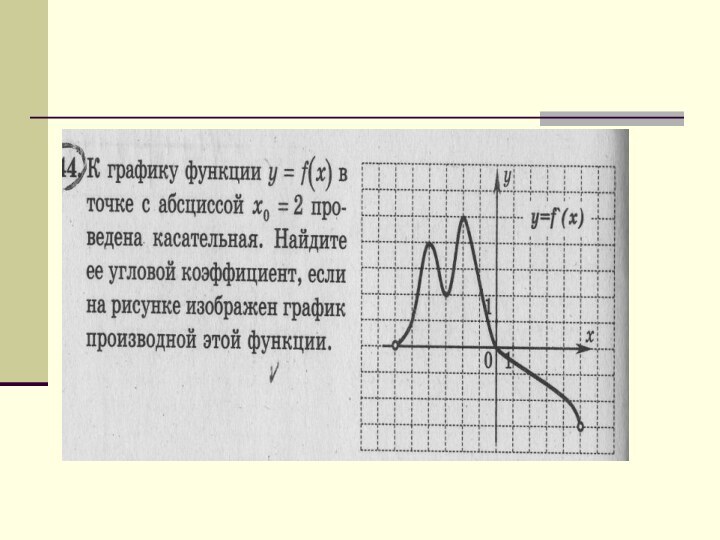
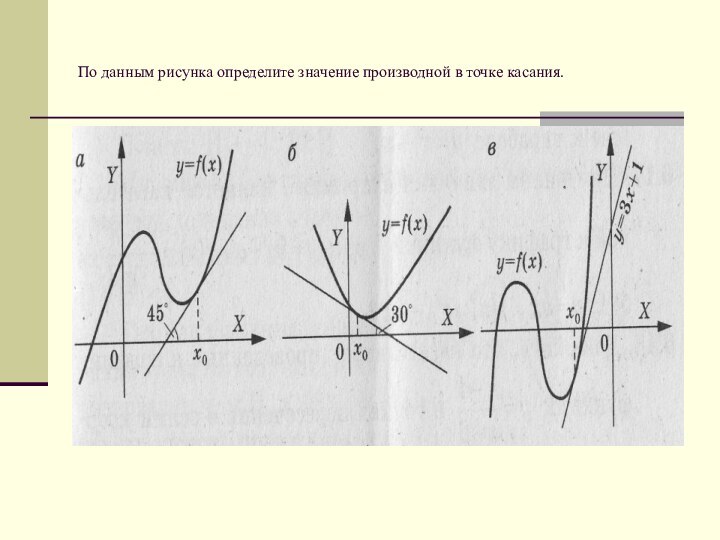
коэффициент касательной к графику функции.
б) Угол ,образованный касательной к
графику функции с положительным направлением оси абсцисс.в) Тангенс угла наклона касательной.
2 Исследовать функцию на монотонность. Находить наименьшее и наибольшее значение функции на промежутке.


![Производная степенной функции. Ее геометрический смысл Найти наименьшее и наибольшее значение функции На промежутке [1; 2]На промежутке (6;](/img/tmb/12/1134536/e2d8ad4f5c196bbc94fb70987547c966-720x.jpg)