Слайд 2
Структура программы
Пояснительная записка
Тематическое планирование
Информационное обеспечение
Приложение
Слайд 3
Пояснительная записка
Предлагаемый курс по
математике рассчитан на учащихся 9 классов. Может быть применен
в классах с любым уровнем подготовки. Продолжительность 12 часов.
Умением решать квадратные уравнения овладевают практически все выпускники средней школы.Но чаще всего учащиеся для нахождения корней уравнения применяют только один единственный способ: через применение формул для вычисления дискриминанта и корней квадратного уравнения. Но есть другие формулы и методы решения, применение которых позволяет более рациональнее и быстрее решать данные уравнения, что поможет учащимся успешнее овладевать программой профильной школы.
Данный курс позволит расширить область математических знаний учащихся по теме за счет изучения новых методов, не входящих в школьный курс математики.
Слайд 4
Цели курса:
Знакомство с новыми методами решения квадратных уравнений
Углубление знаний по теме «Квадратные уравнения»
Развитие математических, интеллектуальных способностей,
навыков исследовательской работы
Создание условий для самореализации личности
Слайд 5
Задачи курса:
Познакомить учащихся с новыми способами решения квадратных
уравнений
Закрепить умения решать уравнения известными способами
Ввести теоремы, позволяющие решать
уравнения нестандартными способами
Продолжить формирование общеучебных навыков, математической культуры
Содействовать формированию интереса к исследовательской деятельности
Создать условия для учащихся в реализации и развитии интереса к предмету математика
Подготовить учащихся к правильному выбору профильного направления
Слайд 6
Данный курс предполагает компактное и четкое
изложение теории вопроса и решение типовых задач. На уроках
будет использоваться фронтальный опрос, который охватывает большую часть учащихся класса, что позволяет развивать точную, лаконичную речь, способность работать в быстром темпе. Основные формы работы с учащимися: лекция с элементами беседы, практическая работа, самостоятельная работа, творческая поисковая работа. Программа мобильна, т.к.дает возможность уменьшить количество задач при успешном усвоении метода, а блочная подача позволит учащемуся, пропустившему урок, приступать к работе, не испытывая затруднений. Отличительной особенностью курса является знакомство с методами решения квадратных уравнений с помощью циркуля и линейки и способом «номограмм».
Слайд 7
Минимальные требования к оснащению курса: раздаточный материал
для проведения практических и самостоятельных работ. Для контроля достижений
используются наблюдение активности учащихся на уроке, тестирование.
В результате изучения курса учащиеся
должны знать:
теоремы о свойствах коэффициентов квадратного уравнения
10 различных способов решения уравнений
различные формулы для решения уравнения
должны уметь:
Уверенно применять формулы, способы, теоремы для решения квадратных уравнений
понимать лексику, связанную с предметом
строить, читать, понимать графики
при вычислении применять устные и письменные приемы
пользоваться современными техническими средствами обучения
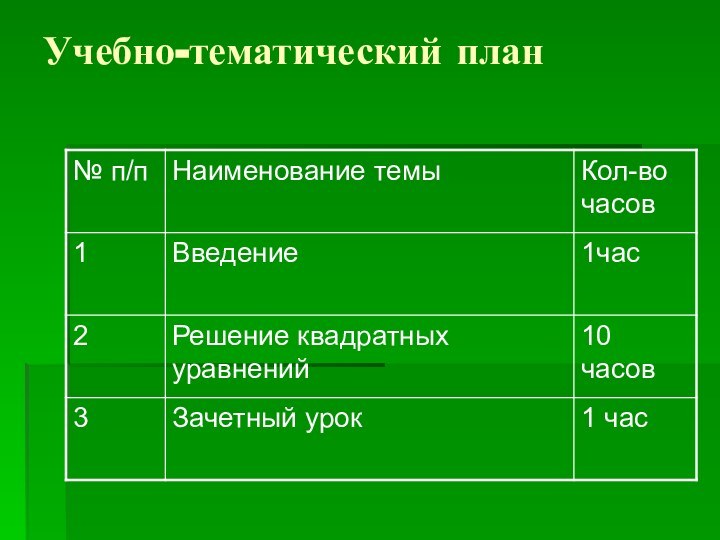
Слайд 9
Содержание программы
Тема 1. Введение. 1 час.
Определение
кв.уравнения. Полные и неполные кв. уравнения. Методы их решения. Анкетирование.
Тема 2. Решение кв. уравнений. 10 часов.
Метод разложения на множители 1 ч.
Метод выделения полного квадрата 1 ч.
Решение кв. уравнений по формулам 1 ч.
Решение кв. уравнений с помощью т.Виета 1 ч.
Решение кв. уравнений способом переброски 1ч.
Решение кв. уравнений с использованием коэффициентом 1ч.
Решение кв. уравнений графическим способом 1 ч.
Решение кв. уравнений с помощью циркуля и линейки 1ч.
Решение кв. уравнений с помощью «номограмм» 1ч.
Решение кв. уравнений геометрическим способом 1ч.
Тема 3. Зачетный урок 1ч.
учителя:
Плужников И.10 способов решения квадратных уравнений//Математика в школе.-2000.-№40
Метельникова Т.П.Устное
решение квадратных уравнений// Математика в школе.-1997.-№10
Математика в школе.-1996.-№21,1997 №10, №24;1998 №18, №21.
Пресман А.А.Решение квадратных уравнений с помощью циркуля и линейки.-М.Квант.№4/72
Для учащихся:
Алгебра 8 класс:ВиленкинН.Я. и др.Учебное пособие для классов с углубленным изучением математики
Алгебра 8 класс:Макарычев Ю.Н. и др.Учебник для общеобразовательных учреждений
Четырехзначные таблицы для средней школы: БрадисВ.М. с 83
Слайд 11
Разложение на множители левой части уравнения
Решим уравнение х2
+ 10х - 24=0.
Разложим на множители левую часть: х2 + 10х - 24= х2 + 12х -2х - 24= х(х + 12) - 2(х + 12)= (х + 12)(х - 2).
(х + 12)(х - 2)=0
х + 12=0 или х - 2=0
х= -12 х= 2
Ответ: х1= -12, х2 = 2.
Решить уравнения: х2 - х=0
х2 + 2х=0
х2 - 81=0
х2 + 4х + 3=0
х2 + 2х - 3=0
Слайд 12
Метод выделения полного квадрата
Решим уравнение х2 +
6х - 7=0
х2 + 6х - 7=х2
+ 2х3 + 32 - 32 - 7=(х-3)2 - 9- 7= (х-3)2 - 16
(х-3)2 -16=0
(х-3)2 =16
х-3=4 или х-3=-4
х=1 х=-7
Ответ: х1=1, х2 =-7.
Решить уравнения: х2 - 8х+15=0
х2 +12х +20=0
х2 + 4х + 3=0
х2 + 2х - 2=0
х2 - 6х + 8=0
Слайд 13
Решение квадратных уравнений по формуле
Основные формулы:
Если b
- нечетное, то D= b2-4ac и х 1,2=
, (если D>0)
Если b- -четное, то D1= и х1,2= , (если D>0)
Решите уравнения: 2х2 - 5х + 2=0
6х2 + 5х +1=0
4х2 - 5х + 2=0
2х2 - 6х + 4=0
х2 - 18х +17=0
=
Слайд 14
Решение уравнений способом переброски
Решим уравнение ах2
+bх+с=0. Умножим обе части уравнения на а, получим а2
х2 +аbх+ас=0. Пусть ах =у, откуда х = у/а. Тогда У2 +bу+ас=0. Его корни у1 и у2 . Окончательно х1 = у1 /а, х1 = у2 /а.
Решим уравнение 2х2 -11х + 15=0.
Перебросим коэффициент 2 к свободному члену:
У2 -11у+30=0.
Согласно теореме Виета у1 =5 и у2 =6.
х1 =5/2 и х2 =6/2
х1 =2,5 и х2 =3
Ответ: х1=2,5 , х2 =3
Решить уравнение: 2х2 -9х +9=0
10х2 -11х + 3=0
3х2 +11х +6=0
6х2 +5х - 6=0
3х2 +1х - 4=0
Слайд 15
Решение уравнений с помощью теоремы Виета
Решим уравнение х2
+10х-24=0.
Так как х1 *х2 =-24
х1 +х2 = -10, то 24= 2*12, но -10=-12+2, значит
х1 =-12 х2 =2
Ответ: х1=2, х2 =-12.
Решить уравнения: х2 - 7х - 30 =0
х2 +2х - 15=0
х2 - 7х + 6=0
3х2 - 5х + 2=0
5х2 + 4х - 9=0
Слайд 16
Свойства коэффициентов квадратного уравнения
Если a+b+c=0, то х2
= 1, х2 = с/а
Если a – b + c=0, то х2 =-1, х2 = -с/а
Решим уравнение х2 + 6х - 7= 0 Решим уравнение 2х2 + 3х +1= 0
1 + 6 – 7 =0, значит х1=1, х2 = -7/1=-7. 2 - 3+1=0, значит х1= - 1, х2 = -1/2
Ответ: х1=1, х2 =-7. Ответ: х1=-1, х2 =-1/2.
Решить уравнения: 5х2 - 7х +2 =0 Решить уравнения: 5х2 - 7х -12 =0
11х2 +25х - 36=0 11х2 +25х +14=0
345х2 -137х -208=0 3х2 +5х +2=0
3х2 +5х - 8=0 5х2 + 4х - 1=0
5х2 + 4х - 9=0 х2 + 4х +3=0
Слайд 17
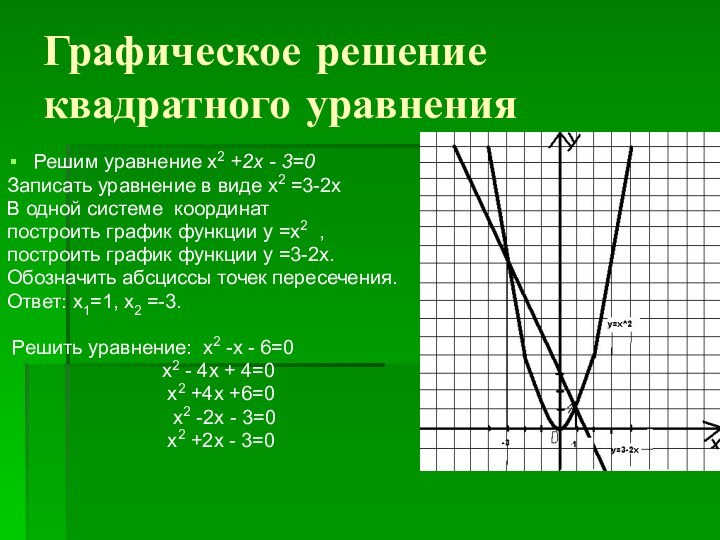
Графическое решение квадратного уравнения
Решим уравнение х2 +2х -
3=0
Записать уравнение в виде х2 =3-2х
В одной системе
координат
построить график функции у =х2 ,
построить график функции у =3-2х.
Обозначить абсциссы точек пересечения.
Ответ: х1=1, х2 =-3.
Решить уравнение: х2 -х - 6=0
х2 - 4х + 4=0
х2 +4х +6=0
х2 -2х - 3=0
х2 +2х - 3=0
Слайд 18
Решение уравнений с помощью циркуля и линейки
Решим уравнение
aх2 +bх+c=0:
Построим точки S(-b:2a,(a+c):2a)- центр окружности и точку А(0,1)
Провести
окружность радиуса SA
Абсциссы точек пересечения с осью Ох есть корни исходного уравнения
Слайд 19
Геометрический способ решения уравнения
Решим уравнение У2 - 6у
- 16=0
Представим в виде У2- 6у = 16. На
рис.
«изображено» выражение У2- 6у , т.е.
из площади квадрата со стороной у
дважды вычитается площадь квадрата
со стороной 3. Значит У2 –6у+9 есть
площадь квадрата со стороной у-3.
Выполнив замену У2- 6у = 16, получим
(у-3)2 =16+9
у-3=5 или у-3=-5
у1 =8 у2 =-2 Решить уравнение У2 +6у - 16=0
Ответ: у1 =8 , у2 =-2