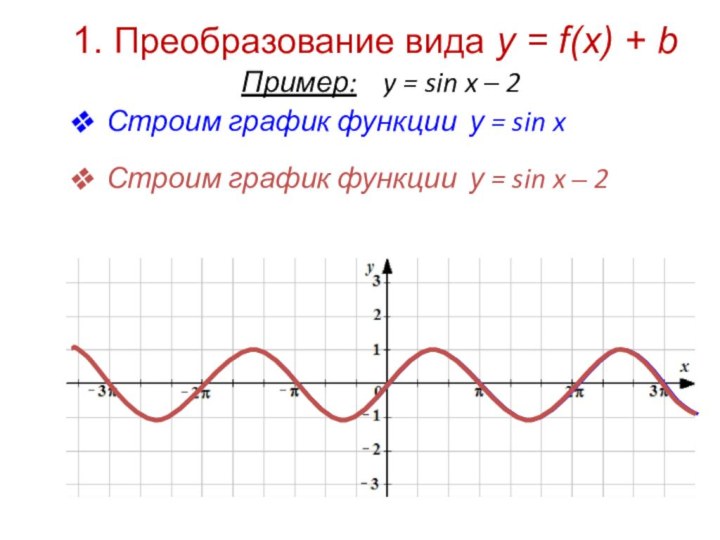
Это параллельный перенос графика функции y = f(x) на
b единиц вдоль оси ординатЕсли b > 0, то
происходит
Если b < 0, то
происходит
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

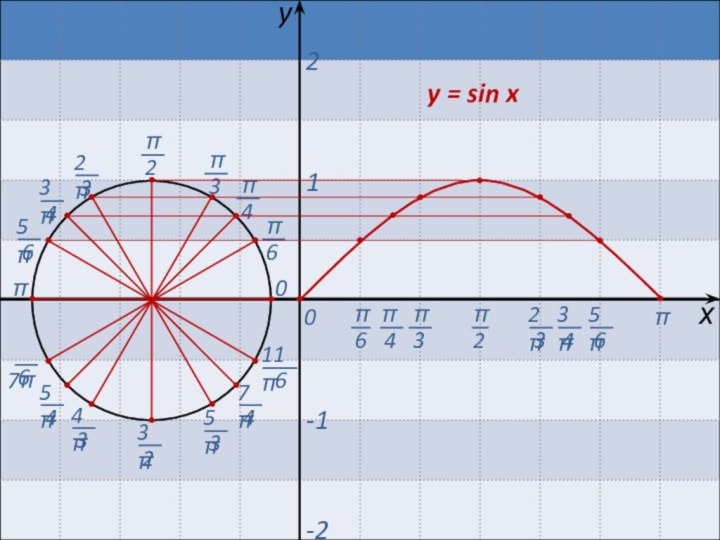
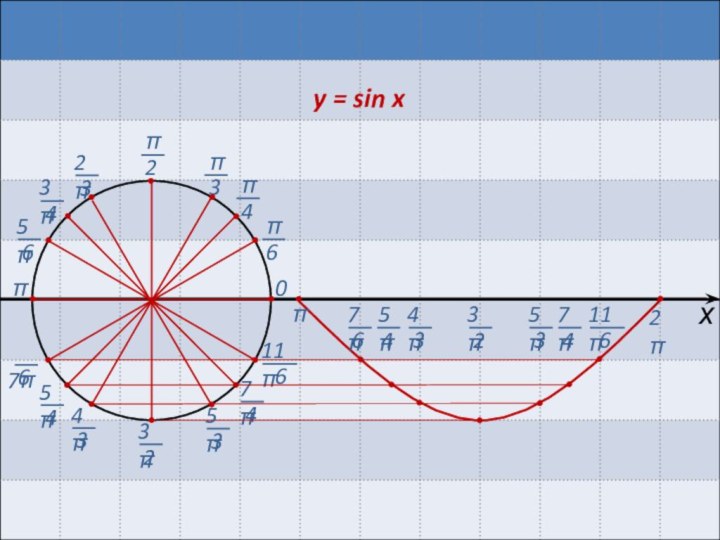
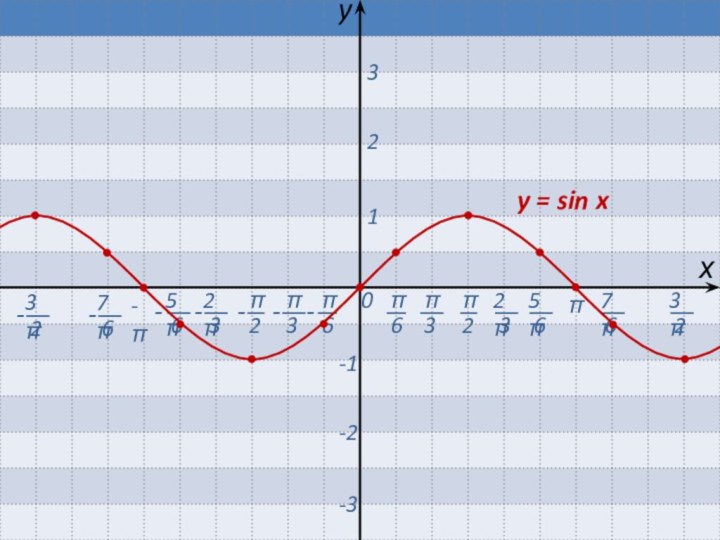
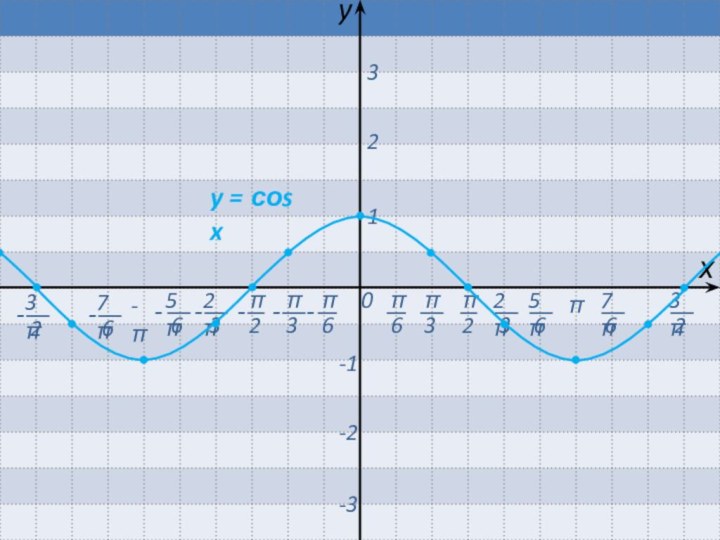
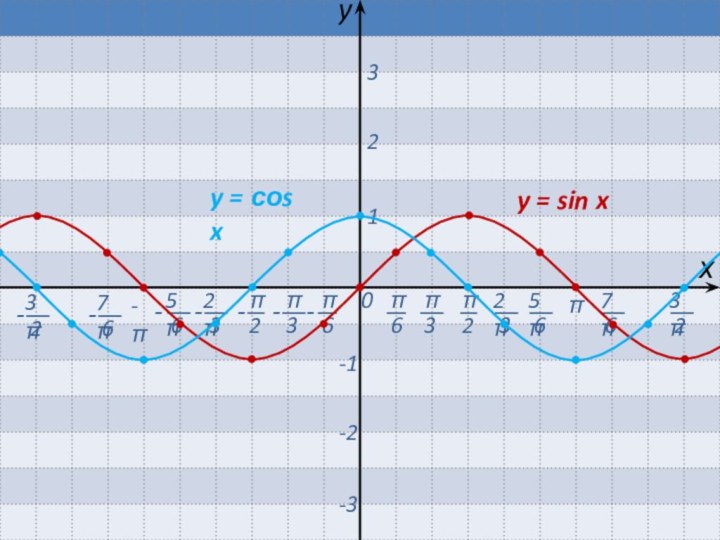
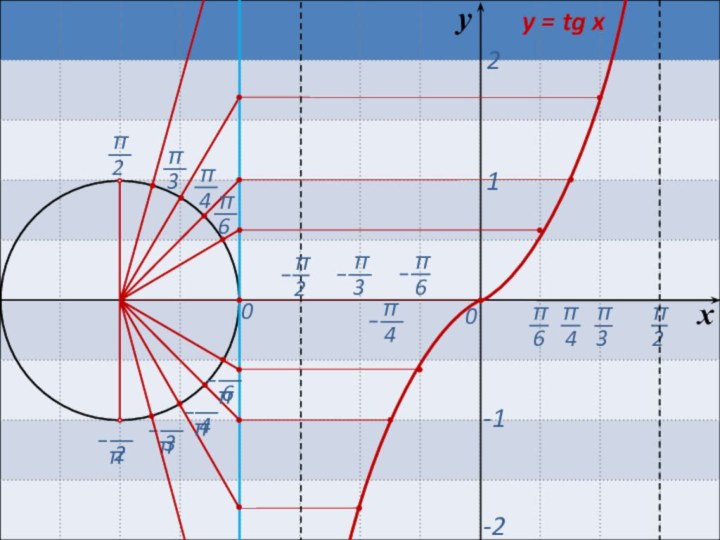
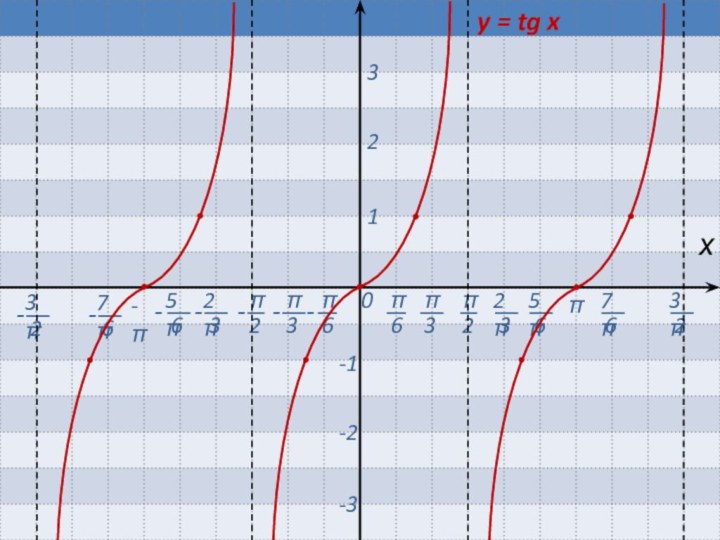
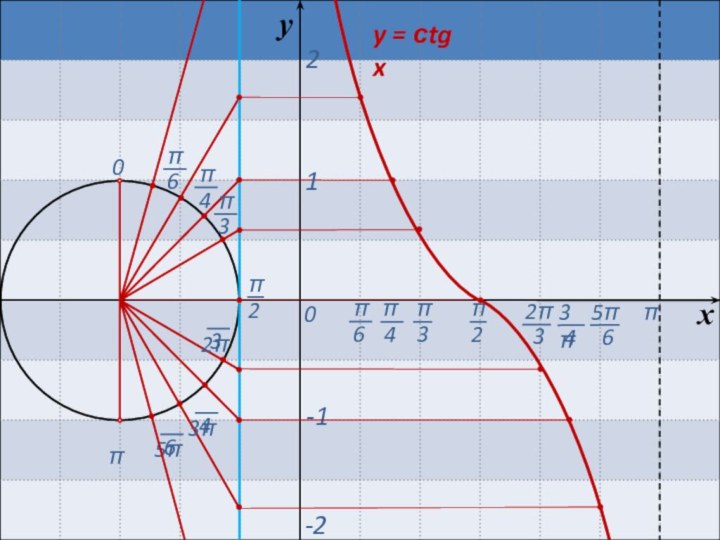
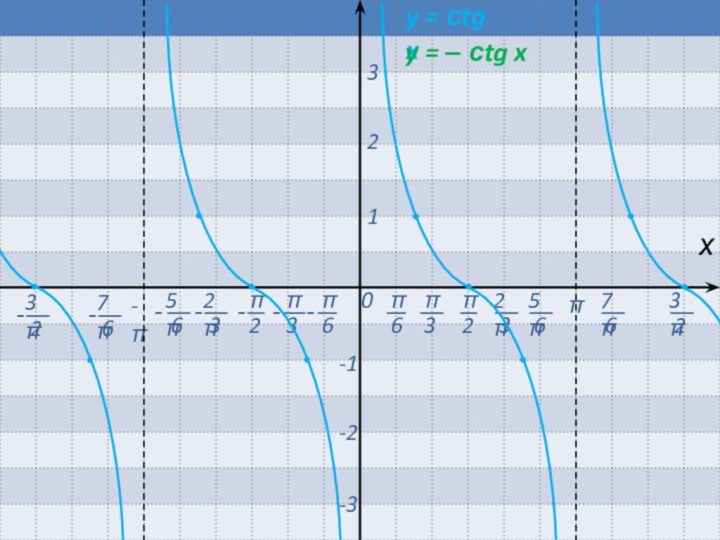




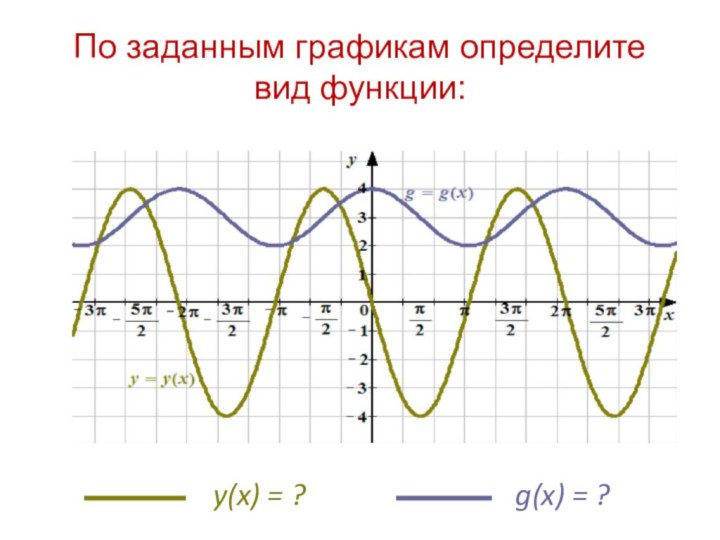
Если b > 0, то
происходит
Если b < 0, то
происходит
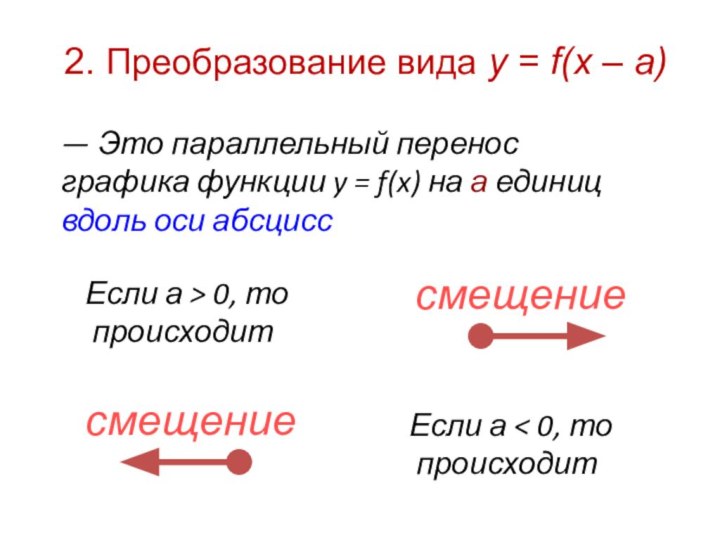
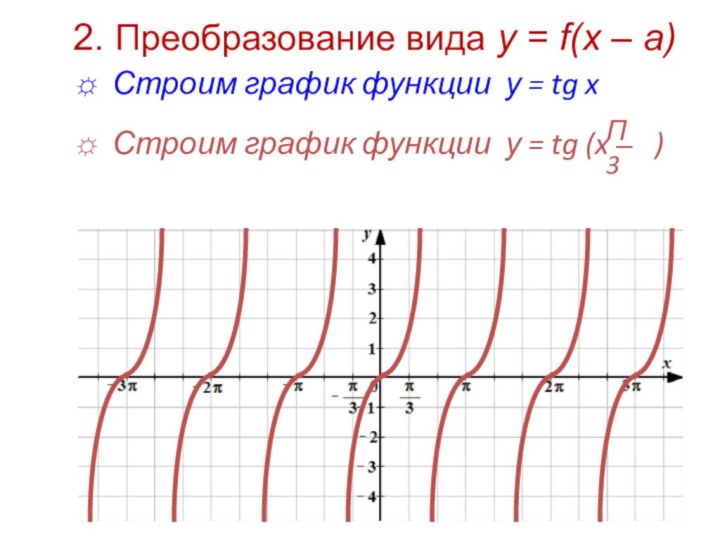
Если а > 0, то
происходит
Если а < 0, то
происходит
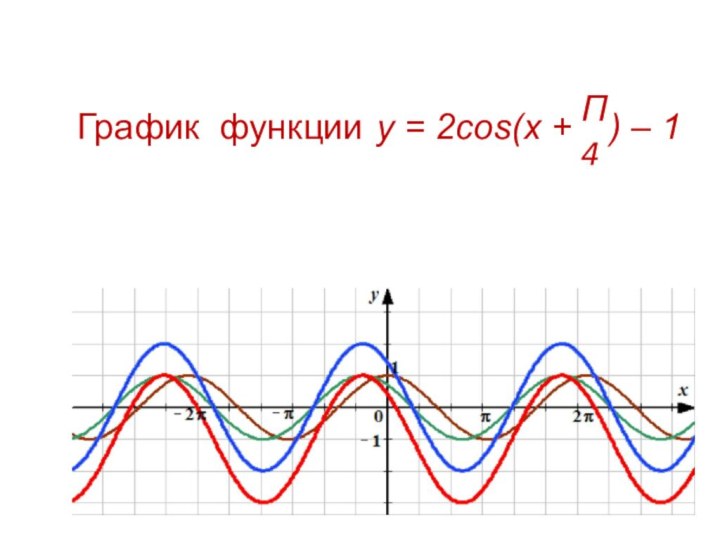
Π
3
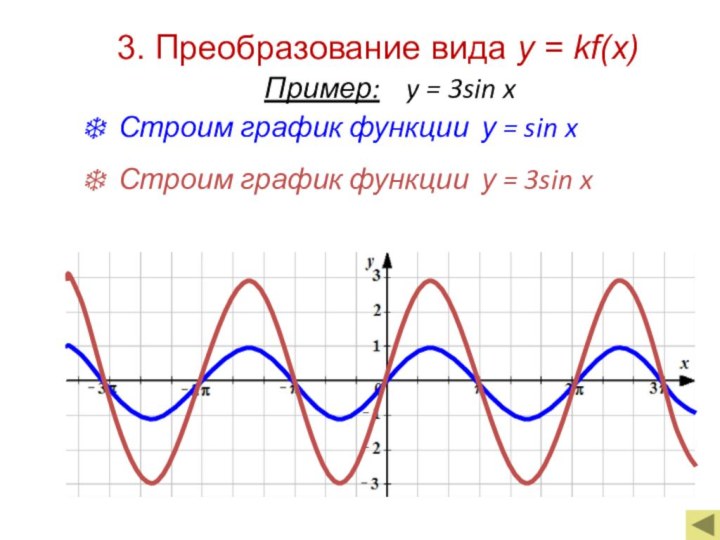
Если k > 1, то
происходит
Если 0 < k < 1, то происходит
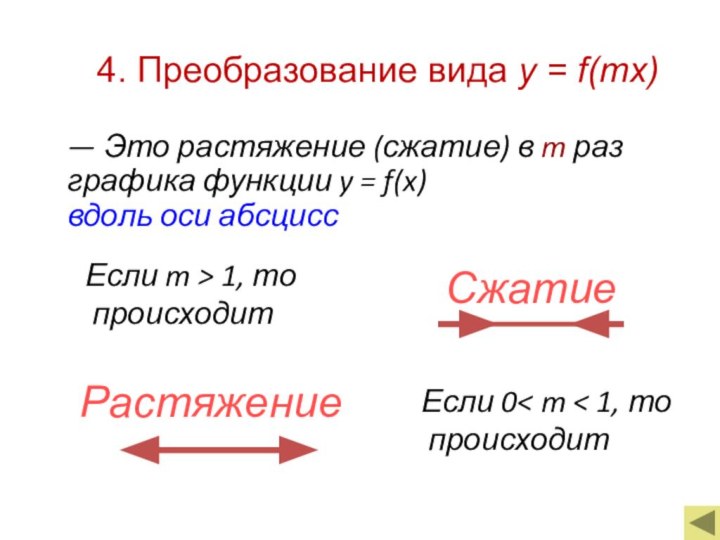
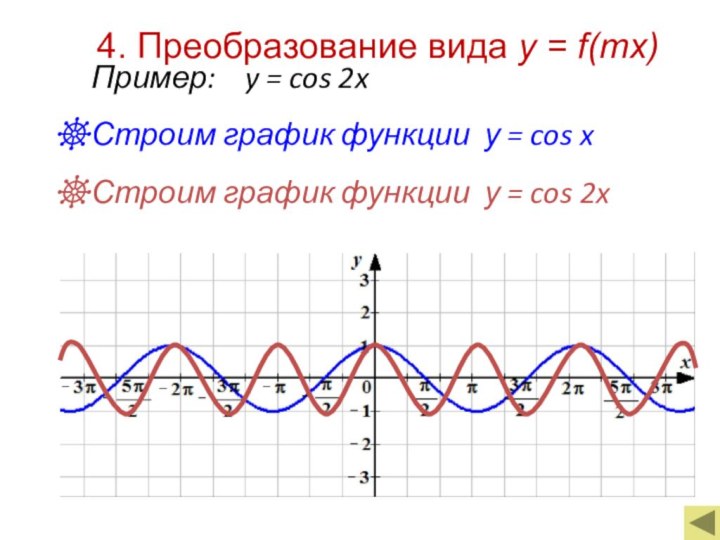
Если m > 1, то
происходит
Если 0< m < 1, то
происходит
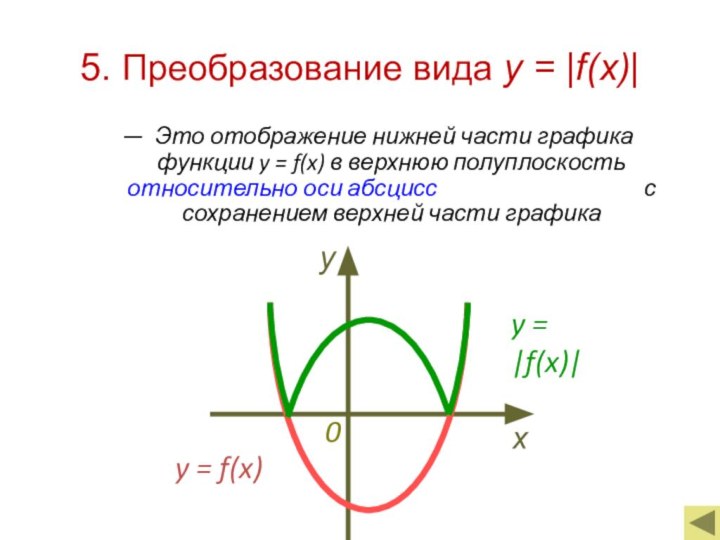
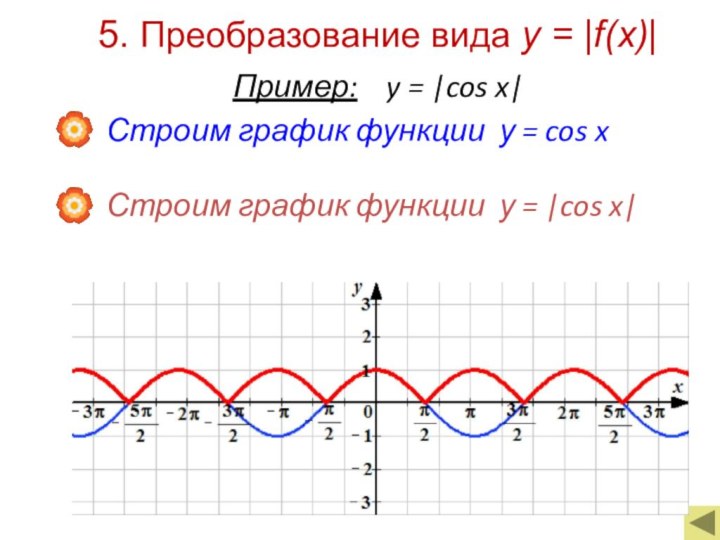
y = f(x)
y = |f(x)|
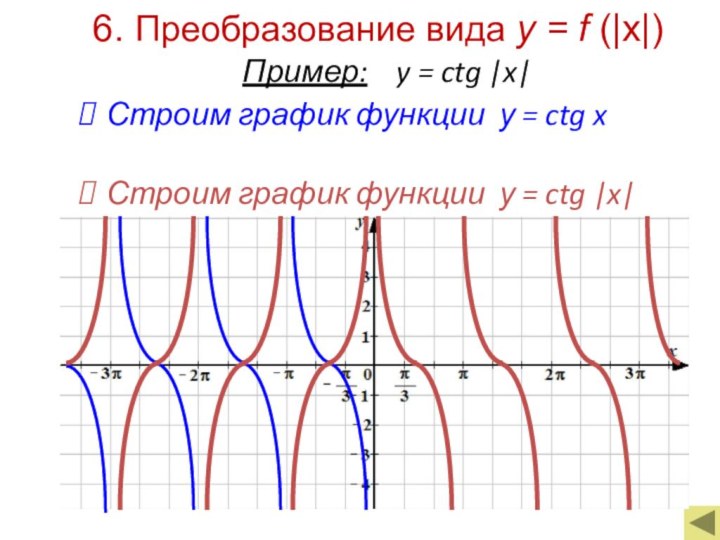
y = f(|x|)
y = f(x)
0