- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства геометрических фигур
Содержание
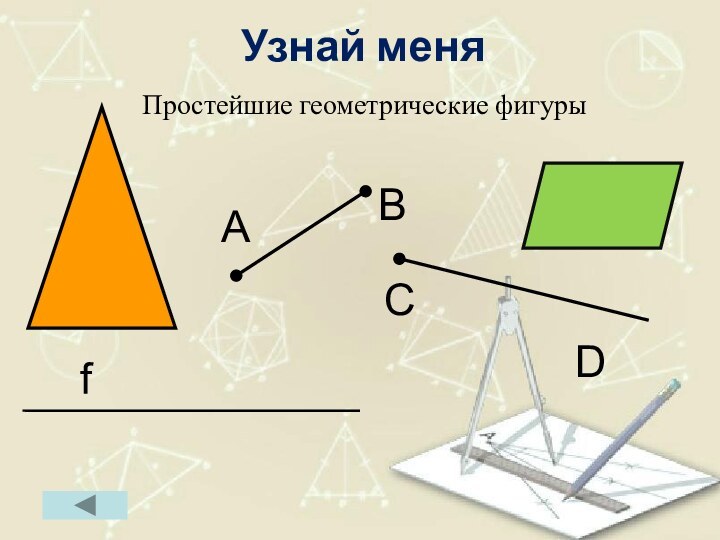
- 2. Узнай меня Простейшие геометрические фигуры АВfDС
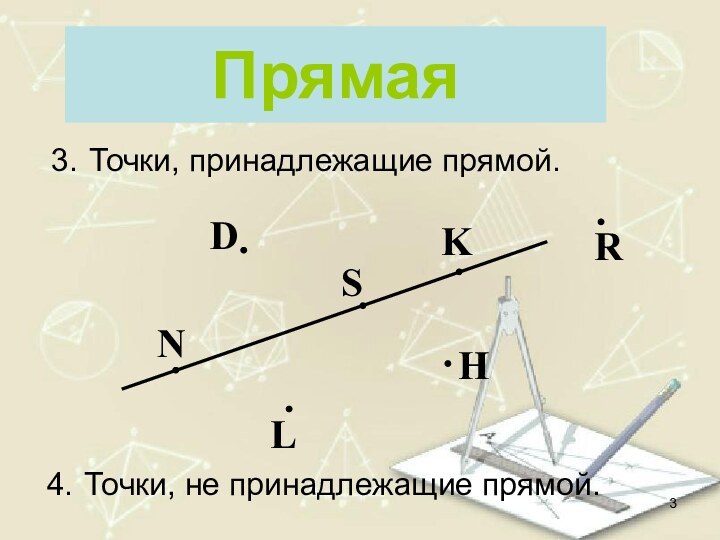
- 3. ПрямаяNKHLDSRТочки, принадлежащие прямой.Точки, не принадлежащие прямой.
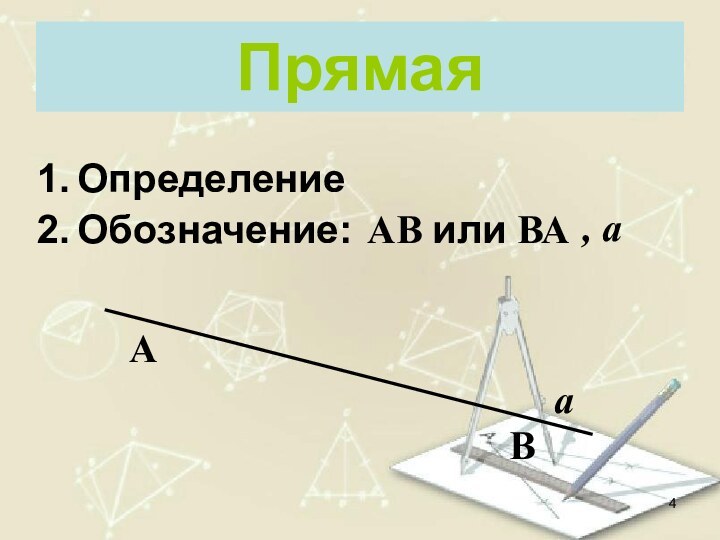
- 4. ПрямаяАВаАВ или ВА, аОпределениеОбозначение:
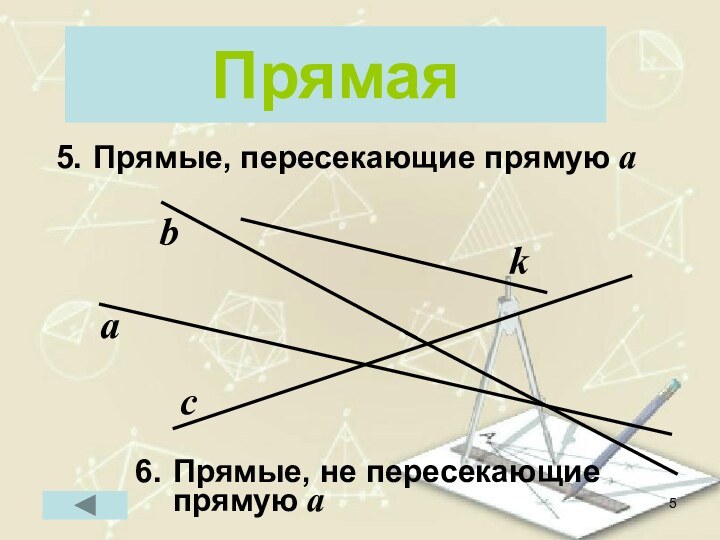
- 5. ПрямаяаcbПрямые, пересекающие прямую аПрямые, не пересекающие прямую аk
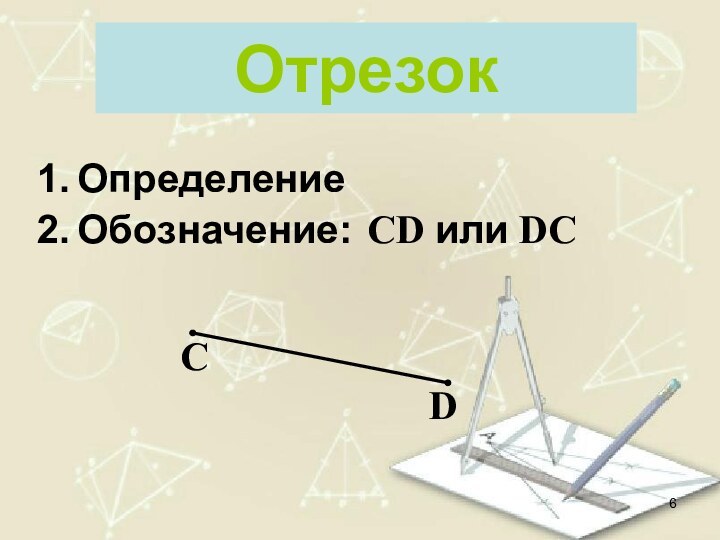
- 6. ОтрезокCDCD или DCОпределениеОбозначение:
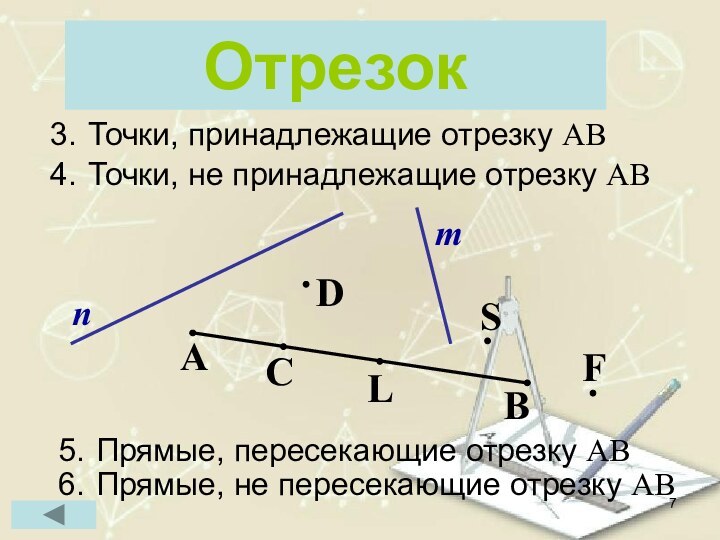
- 7. ОтрезокАВnmCDSLFТочки, принадлежащие отрезку АВТочки, не принадлежащие отрезку АВПрямые, пересекающие отрезку АВПрямые, не пересекающие отрезку АВ
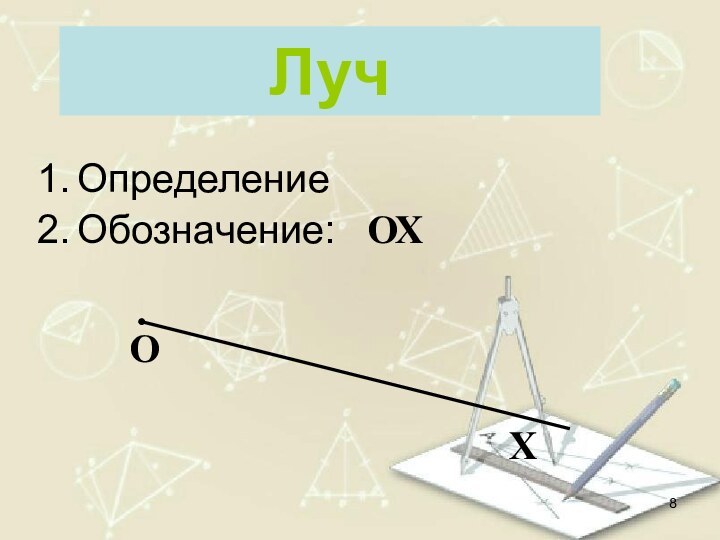
- 8. ЛучОХОХОпределениеОбозначение:
- 9. ЛучKLТочки, принадлежащие лучу KLCADOТочки, не принадлежащие лучу KLЛучи, пересекающие луч KLЛучи, не пересекающие луч KLВST
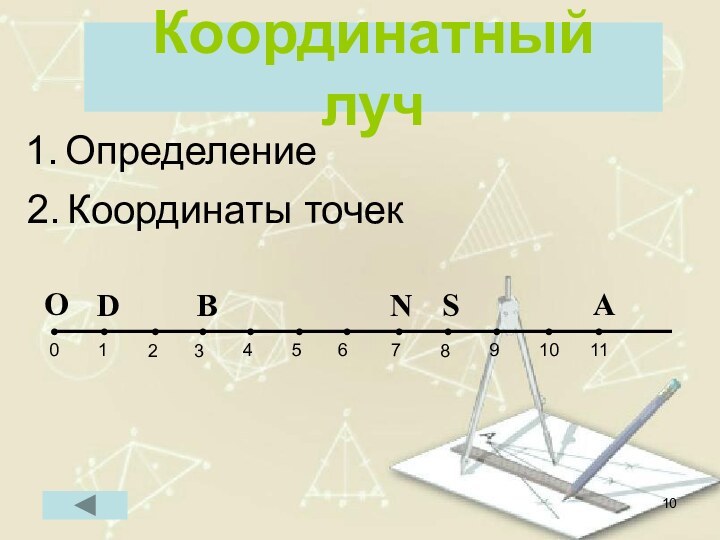
- 10. Координатный лучОпределениеКоординаты точек
- 11. Треугольник Треугольник - простейшая плоская фигура.
- 12. Первое упоминание о треугольнике и его свойствах
- 13. Виды треугольников по угламОстроугольный треугольникПрямоугольный треугольникТупоугольный треугольникНачало
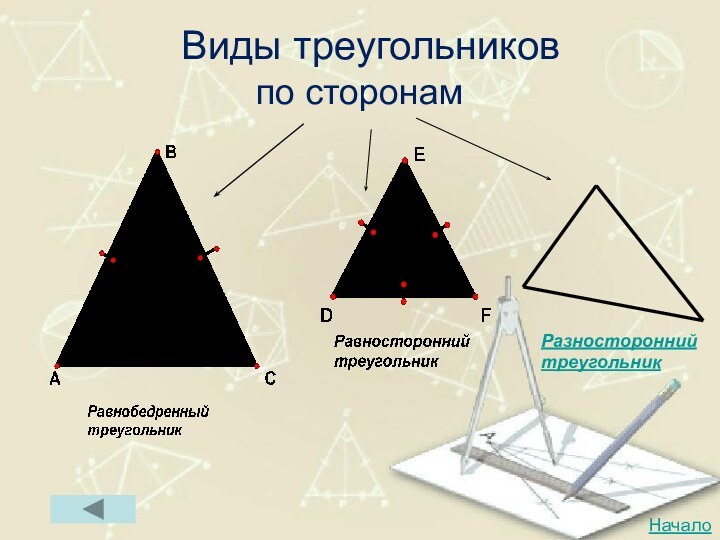
- 14. Виды треугольников по сторонамНачалоРазносторонний треугольник
- 15. Отрезки треугольникаМедиана треугольникаВысота треугольникаБиссектриса треугольникаПроверочные заданияНачало
- 16. ТреугольникиПризнаки равенства треугольниковПризнаки подобия треугольниковПризнаки равенства прямоугольных треугольниковРешение задачНачало
- 17. Прямоугольные треугольники Треугольник, у которого есть прямой
- 18. Тупоугольные треугольники Треугольник, у которого есть тупой
- 19. Остроугольные треугольники Треугольник, у которого все углы острые, называется остроугольным.Это – остроугольные треугольники.
- 20. 4. Равнобедренные треугольники Треугольник, у которого есть
- 21. Равносторонние треугольники Треугольник, у которого все стороны
- 22. Разносторонние треугольники Треугольник, у которого все стороны
- 23. Медиана треугольникаОтрезок соединяющий вершину треугольника с серединой
- 24. Высота треугольникаПерпендикуляр проведенный из вершины треугольника к
- 25. Биссектриса треугольникаОтрезок биссектрисы угла треугольника, соединяющий вершину
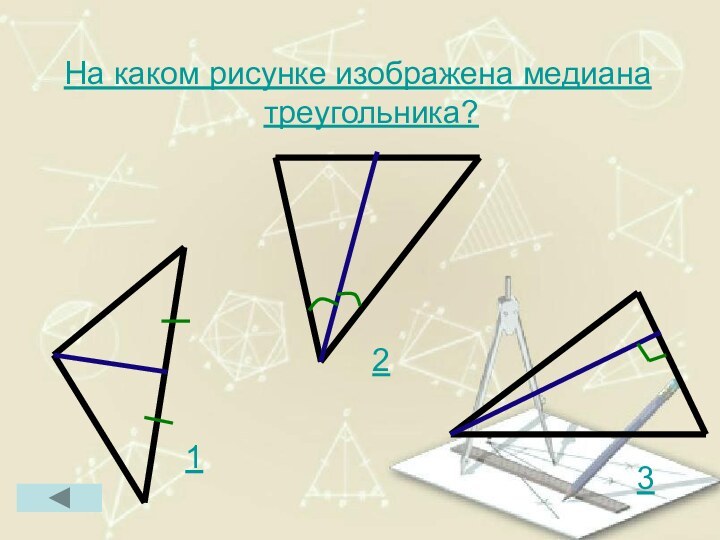
- 26. На каком рисунке изображена медиана треугольника?123
- 27. Подумай ещё!
- 28. Подумай ещё!
- 29. Молодец!
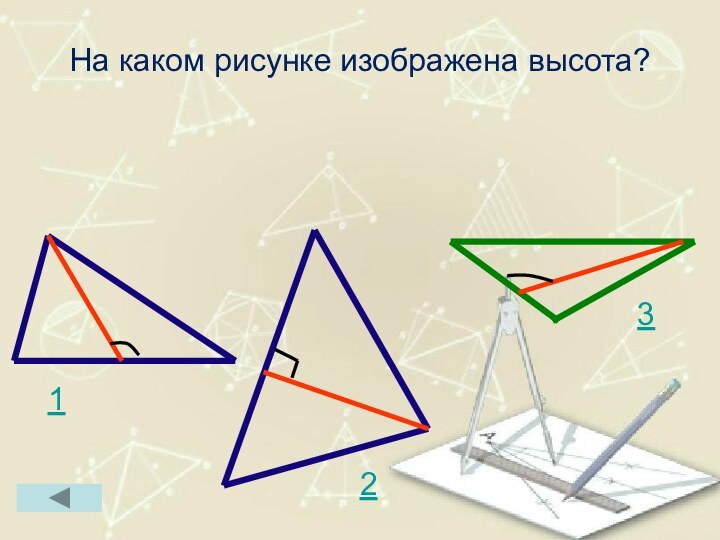
- 30. На каком рисунке изображена высота?123
- 31. Подумай ещё!
- 32. Подумай ещё!
- 33. Молодец!
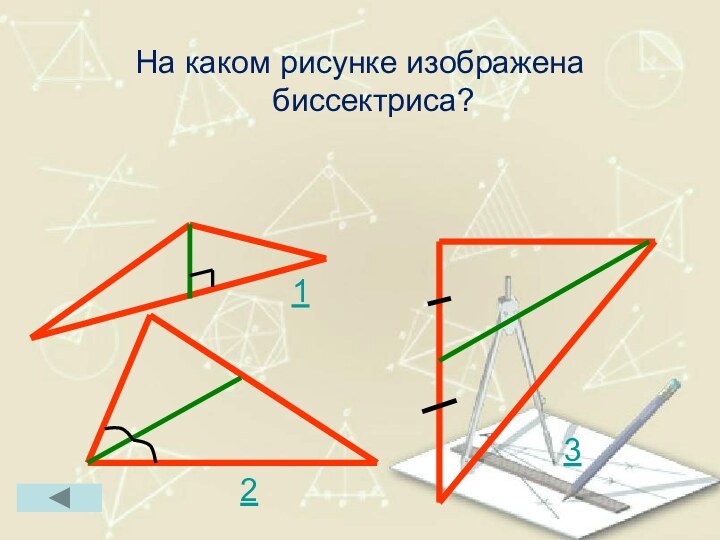
- 34. На каком рисунке изображена биссектриса?123
- 35. Подумай ещё!
- 36. Подумай ещё!
- 37. Молодец!
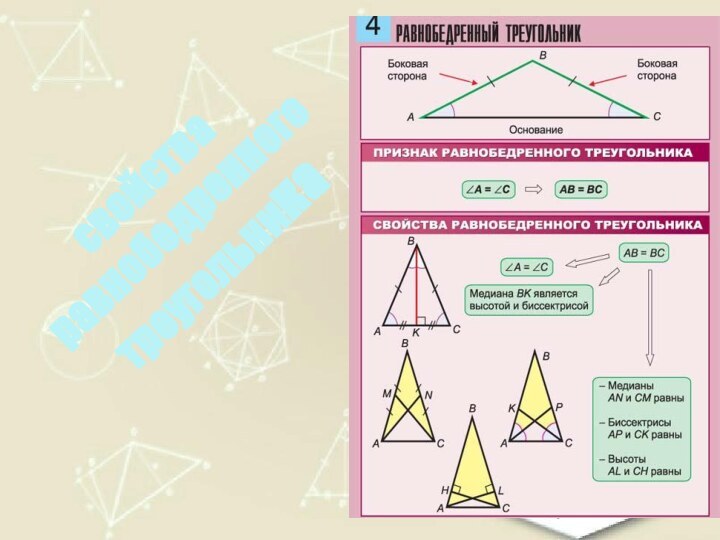
- 38. свойстваравнобедренноготреугольника
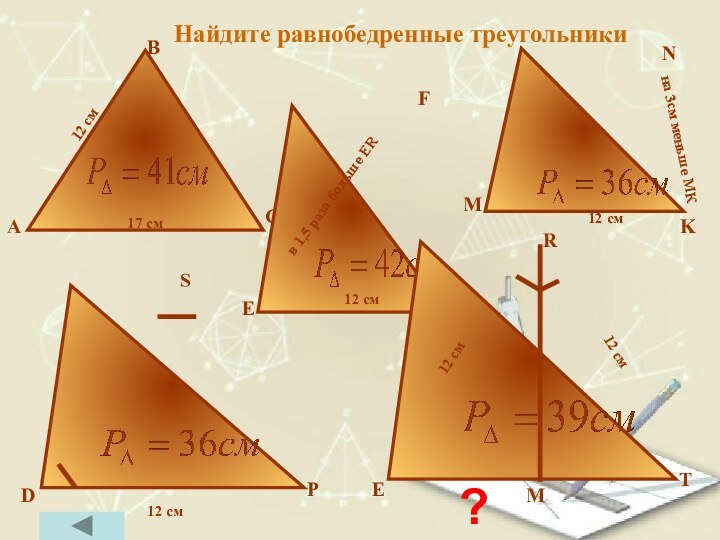
- 39. Найдите равнобедренные треугольники
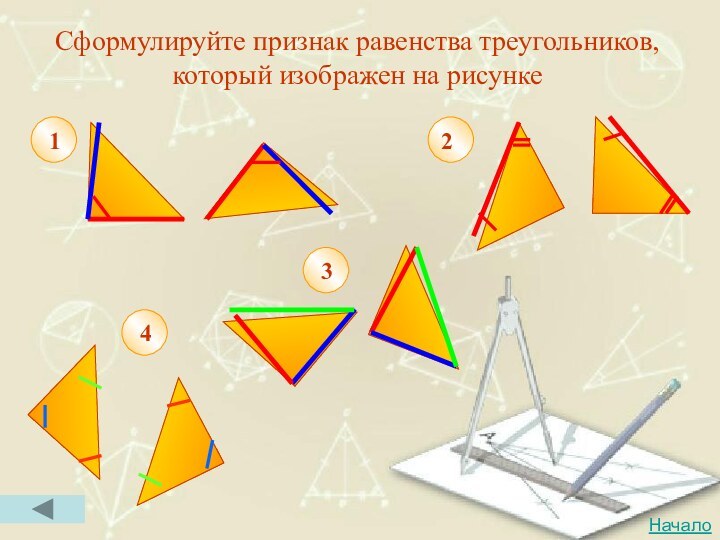
- 40. Сформулируйте признак равенства треугольников, который изображен на рисунке2431Начало
- 41. Первый признак равенства треугольникови углу между ними)(по
- 42. Второй признак равенства треугольникови двум прилежащим к
- 43. Третий признак равенства треугольников(по трем сторонам)назадЕсли три
- 44. Такого признака равенства треугольников не существуетназадЭто подобие
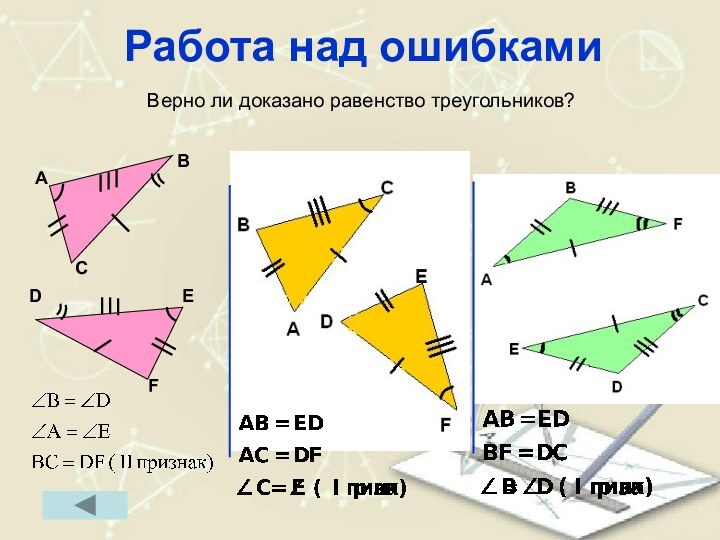
- 45. Работа над ошибкамиВерно ли доказано равенство треугольников?
- 46. Задачи с практическим содержаниемЗадача Лежащий на полу
- 47. Указания к решению задач с практическим содержаниемЗадача Докажите равенство ∆ AFE и ∆ CDE.43
- 48. Указания к решению задач с практическим содержаниемЗадача Докажите равенство ∆ AFE и ∆ CDE.433455
- 49. Самостоятельная работаНайдите на рисунках равные треугольники и докажите их равенствоРис.1Рис.2Рис.3
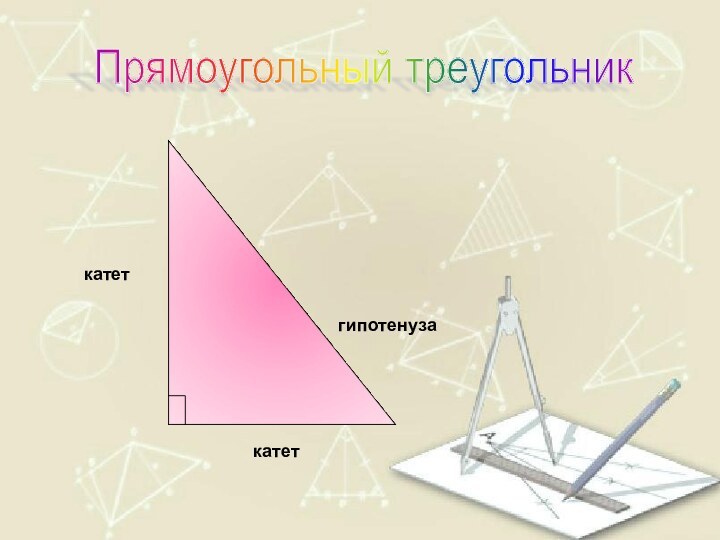
- 50. катет
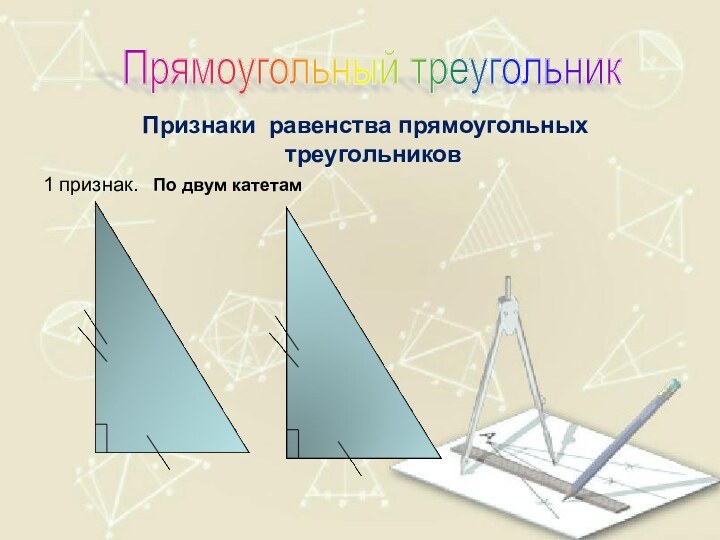
- 51. Признаки равенства прямоугольных треугольников1 признак. По двум катетамПрямоугольный треугольник
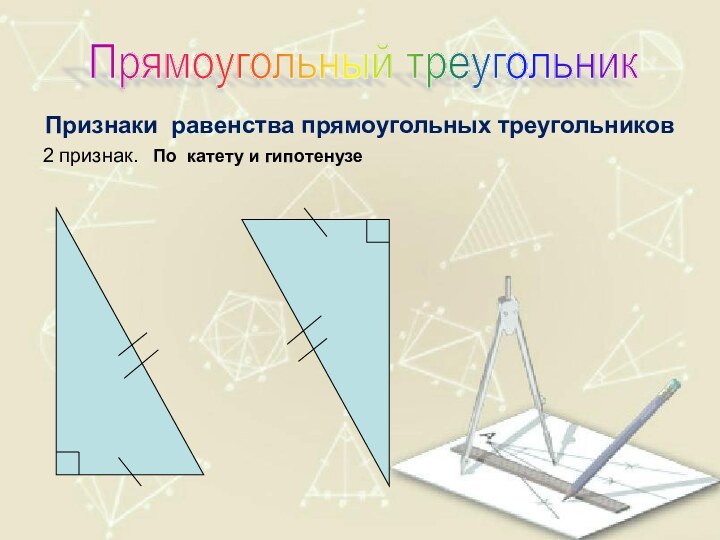
- 52. Признаки равенства прямоугольных треугольников2 признак. По катету и гипотенузеПрямоугольный треугольник
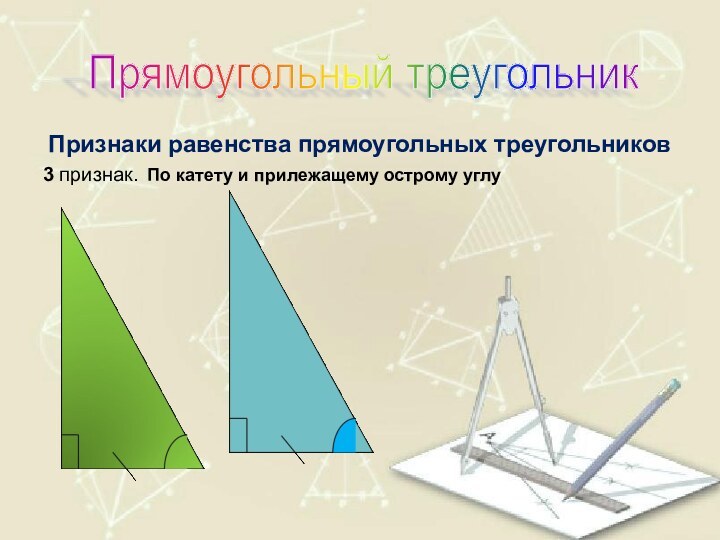
- 53. Признаки равенства прямоугольных треугольников3 признак. По катету и прилежащему острому углуПрямоугольный треугольник
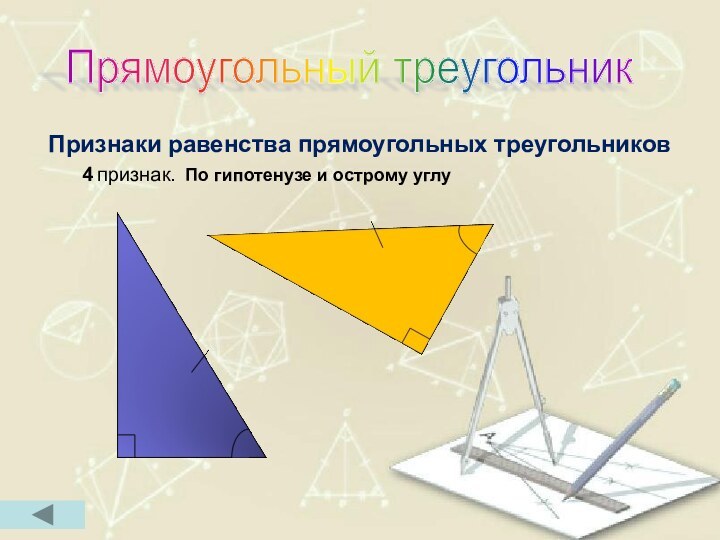
- 54. Признаки равенства прямоугольных треугольников 4 признак. По гипотенузе и острому углуПрямоугольный треугольник
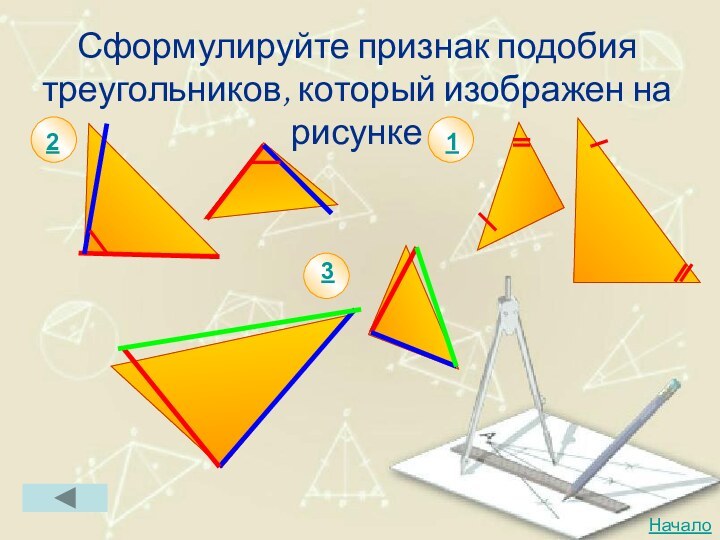
- 55. Сформулируйте признак подобия треугольников, который изображен на рисунке231Начало
- 56. Первый признак подобия треугольников(по двум углам)назадЕсли два
- 57. Второй признак подобия треугольников(по двум сторонам и
- 58. Третий признак подобия треугольников(по трем сторонам)назадЕсли три
- 59. Четырехугольник Четырехугольник – фигура,
- 60. Выпуклость Четырехугольники бывают выпуклыми и невыпуклыми.
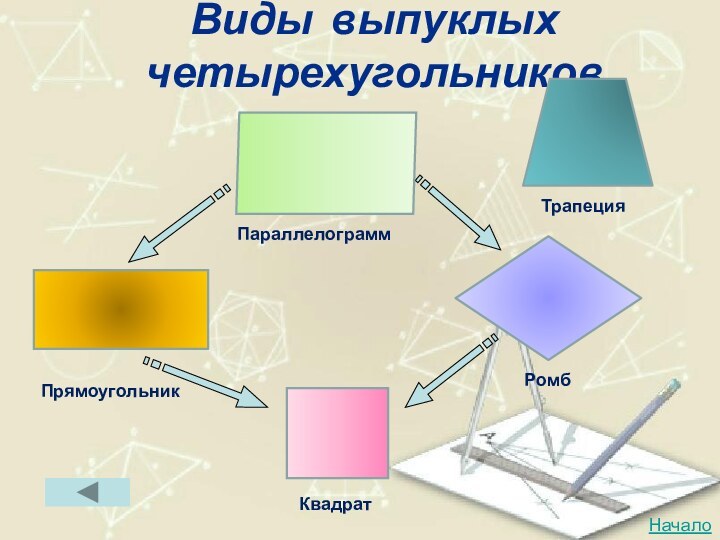
- 61. Виды выпуклых четырехугольниковПараллелограммПрямоугольникКвадратРомбТрапецияНачало
- 62. Площади плоских фигур:Определение площадиСвойства площадейФормулы площадей четырёхугольниковЗакрепление материалаНачало
- 63. Параллелограмм Определение: Параллелограмм – четырехугольник, у которого противолежащие стороны параллельны.Свойства параллелограмма
- 64. Свойства параллелограмма1)Диагонали параллелограмма пересекаются и точкой пересечения
- 65. Прямоугольник Определение: Прямоугольник – это параллелограмм, у которого все углы прямые. Свойствапрямоугольника
- 66. Свойства прямоугольника:Свойства параллелограмма.Диагонали прямоугольника равны. Признак прямоугольника:
- 67. Ромб Определение:Ромб – это параллелограмм, у которого все стороны равны.Свойства ромба
- 68. Свойства ромба:Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.
- 69. Квадрат Определение:1)Квадрат – это прямоугольник, у которого
- 70. Свойства квадратаУ квадрата все углы прямые.2) Диагонали
- 71. ТрапецияОпределение: Трапеция - это
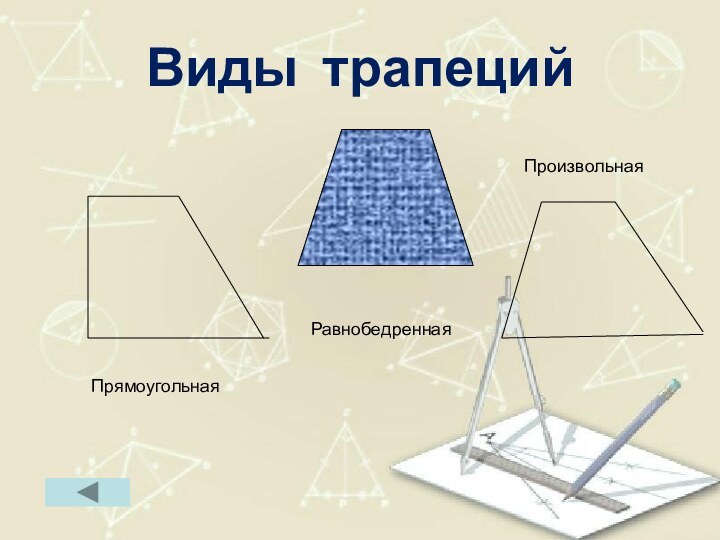
- 72. Виды трапецийПрямоугольнаяРавнобедреннаяПроизвольная
- 73. Понятие площади Что принимают за единицу измерения
- 74. Свойства площадейРавные многоугольники имеют равные площадиЕсли многоугольник
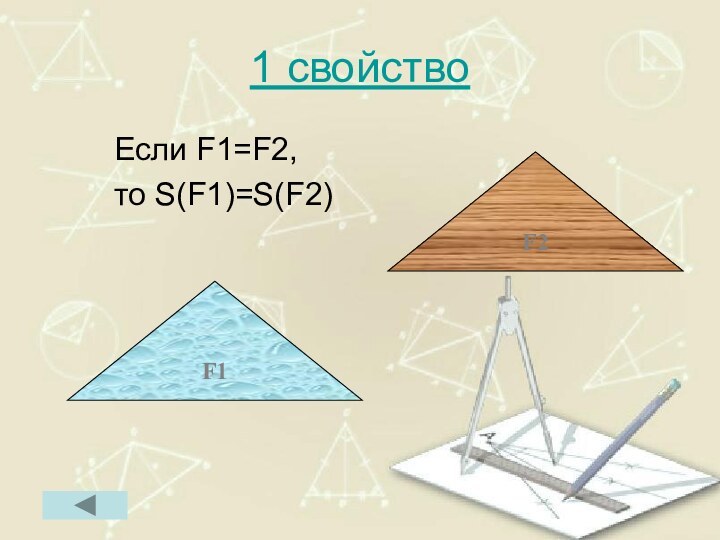
- 75. 1 свойство Если F1=F2, то S(F1)=S(F2)F1F2
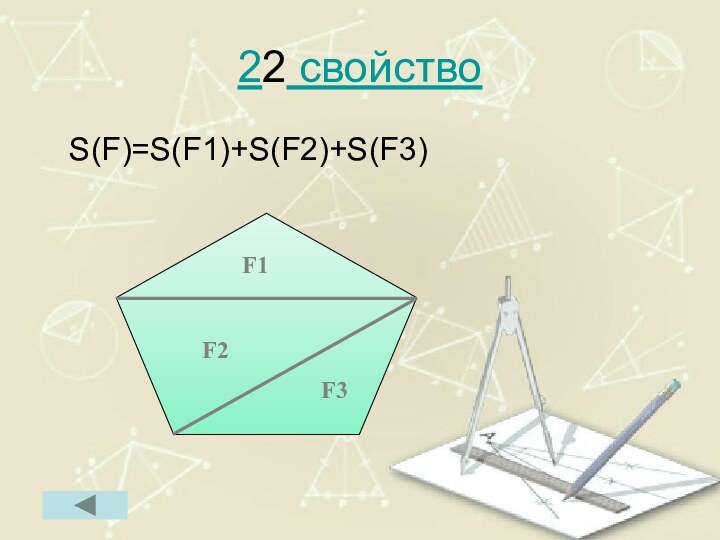
- 76. 22 свойство S(F)=S(F1)+S(F2)+S(F3)F3F2F1
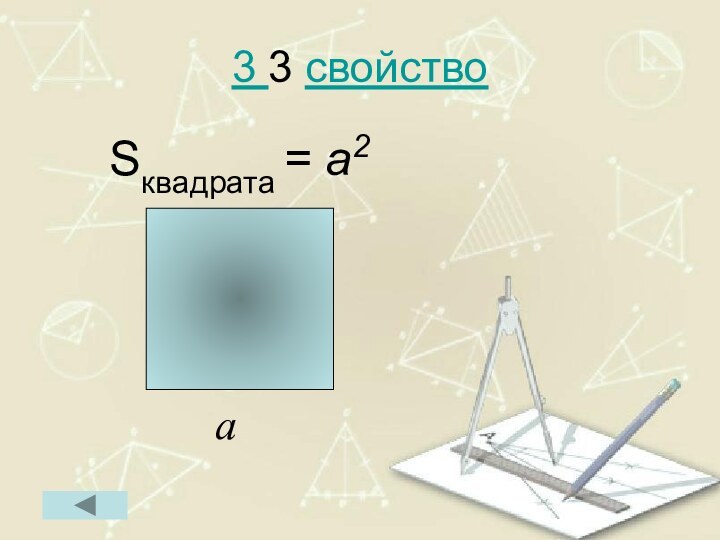
- 77. 3 3 свойство Sквадрата = a2а
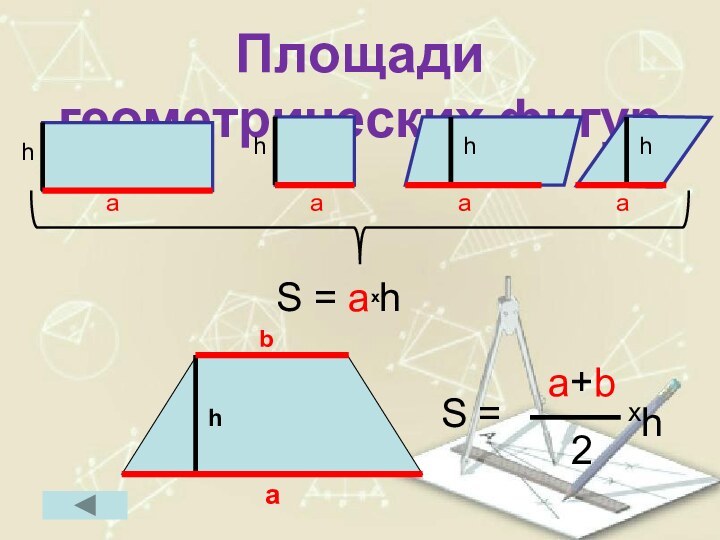
- 78. Площади геометрических фигур
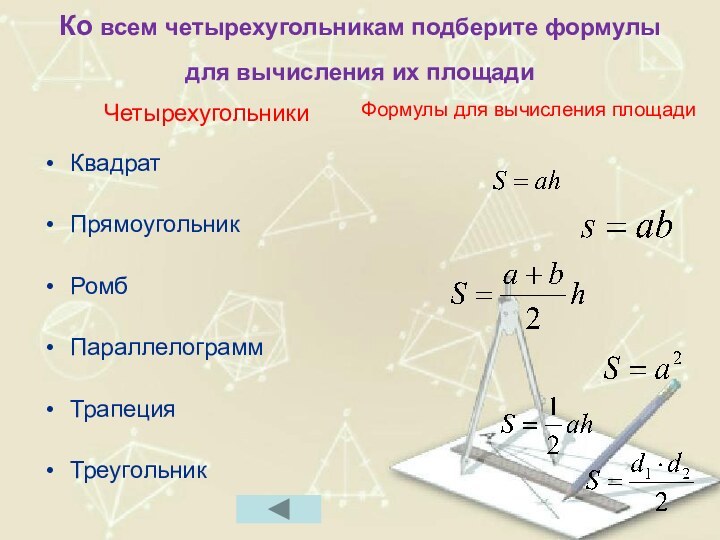
- 79. Ко всем четырехугольникам подберите формулы для вычисления
- 80. Скачать презентацию
- 81. Похожие презентации
Узнай меня Простейшие геометрические фигуры АВfDС






















Слайд 7
Отрезок
А
В
n
m
C
D
S
L
F
Точки, принадлежащие отрезку АВ
Точки, не принадлежащие отрезку АВ
Прямые,
пересекающие отрезку АВ
Слайд 9
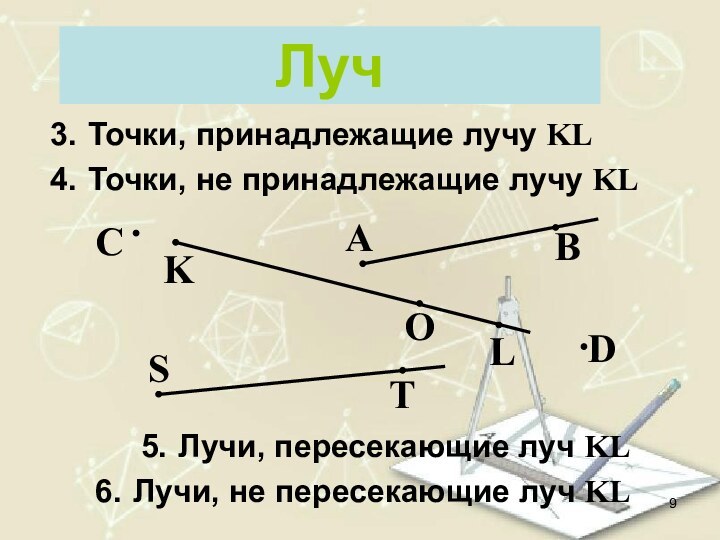
Луч
K
L
Точки, принадлежащие лучу KL
C
A
D
O
Точки, не принадлежащие лучу KL
Лучи,
пересекающие луч KL
Лучи, не пересекающие луч KL
В
S
T
Слайд 11
Треугольник
Треугольник - простейшая плоская фигура. Три
вершины и три стороны. Изучение треугольника породило науку –
тригонометрию. Эта наука возникла из практических потребностей при измерении земельных участков, составлении карт на местности, конструировании машин и механизмов.Слайд 12 Первое упоминание о треугольнике и его свойствах мы
находим в египетских папирусах,
которым более 4000лет,а через
2000 лет - в древней Греции.
Слайд 13
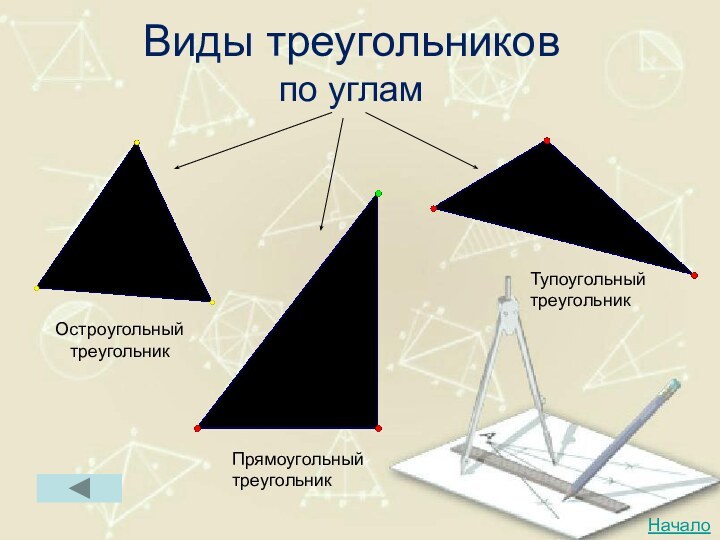
Виды треугольников
по углам
Остроугольный
треугольник
Прямоугольный
треугольник
Тупоугольный
треугольник
Начало
Слайд 15
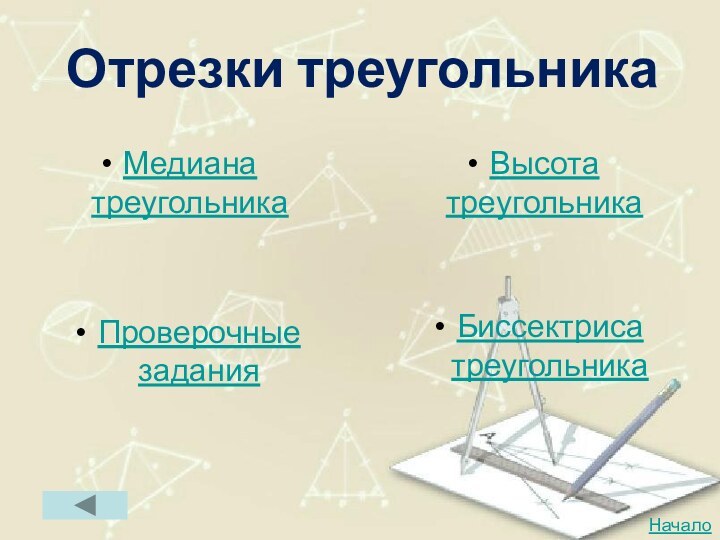
Отрезки треугольника
Медиана треугольника
Высота треугольника
Биссектриса треугольника
Проверочные задания
Начало
Слайд 16
Треугольники
Признаки равенства треугольников
Признаки подобия треугольников
Признаки равенства прямоугольных треугольников
Решение
задач
Начало
Слайд 17
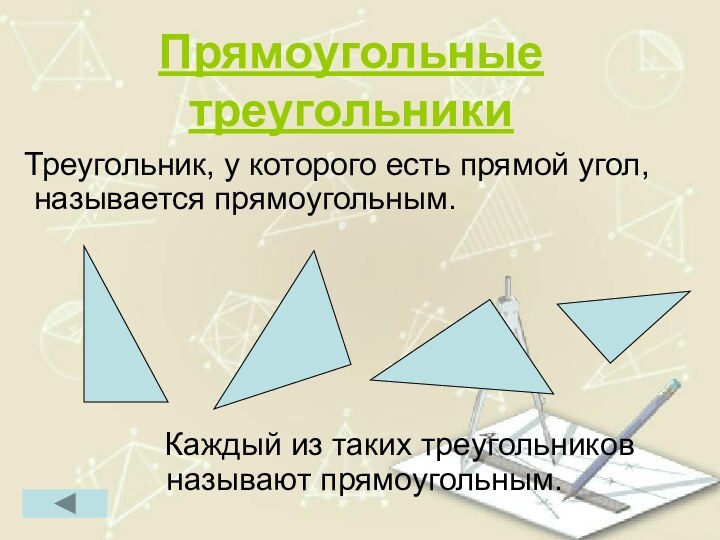
Прямоугольные треугольники
Треугольник, у которого есть прямой угол,
называется прямоугольным.
Каждый из
таких треугольников называют прямоугольным.
Слайд 18
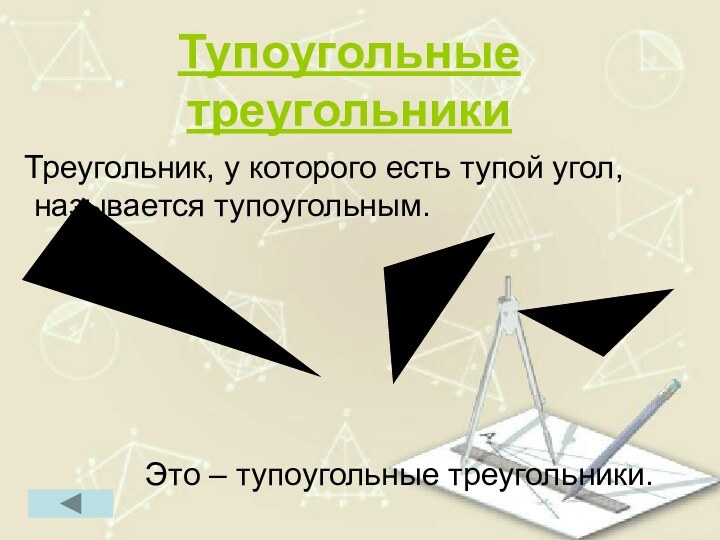
Тупоугольные треугольники
Треугольник, у которого есть тупой угол,
называется тупоугольным.
Это –
тупоугольные треугольники.
Слайд 19
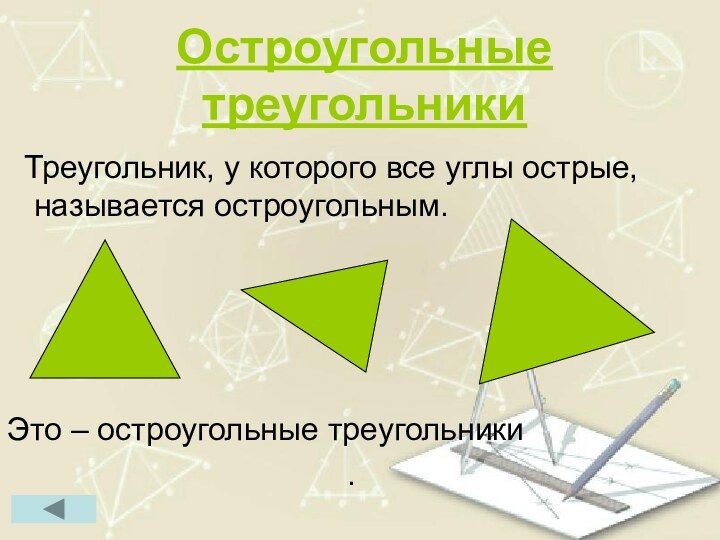
Остроугольные треугольники
Треугольник, у которого все углы острые,
называется остроугольным.
Это – остроугольные треугольники
.
Слайд 20
4. Равнобедренные треугольники
Треугольник, у которого есть равные
стороны, называется равнобедренным.
Каждый
из таких треугольников - равнобедренный.
Слайд 21
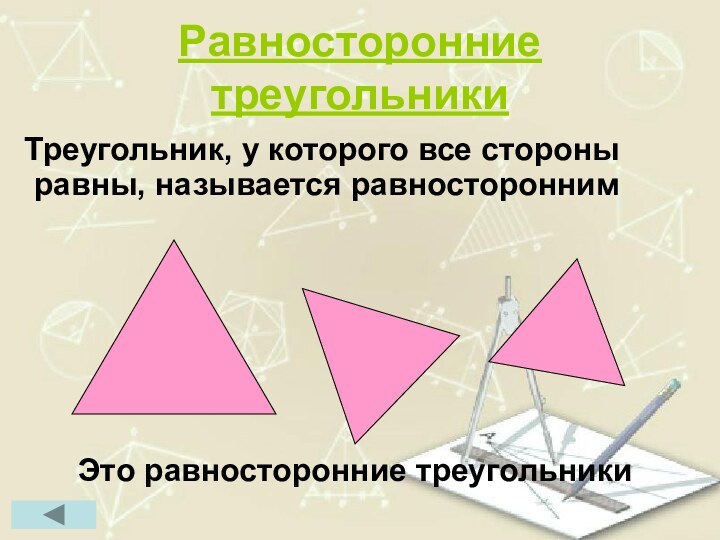
Равносторонние треугольники
Треугольник, у которого все стороны равны,
называется равносторонним
Это равносторонние
треугольники
Слайд 22
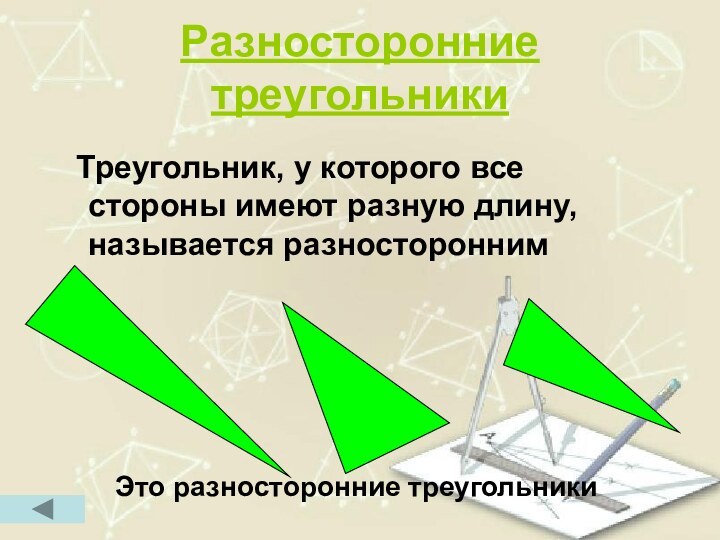
Разносторонние треугольники
Треугольник, у которого все стороны имеют
разную длину, называется разносторонним
Это разносторонние
треугольники
Слайд 23
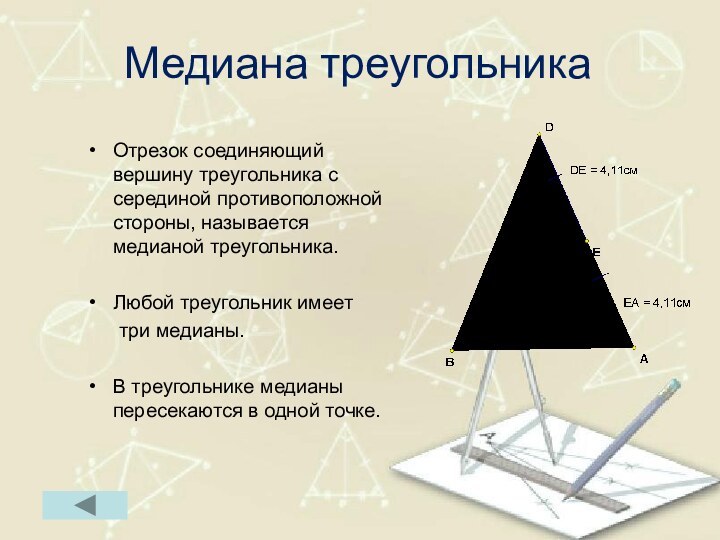
Медиана треугольника
Отрезок соединяющий вершину треугольника с серединой противоположной
стороны, называется медианой треугольника.
Любой треугольник имеет
три медианы.В треугольнике медианы пересекаются в одной точке.
Слайд 24
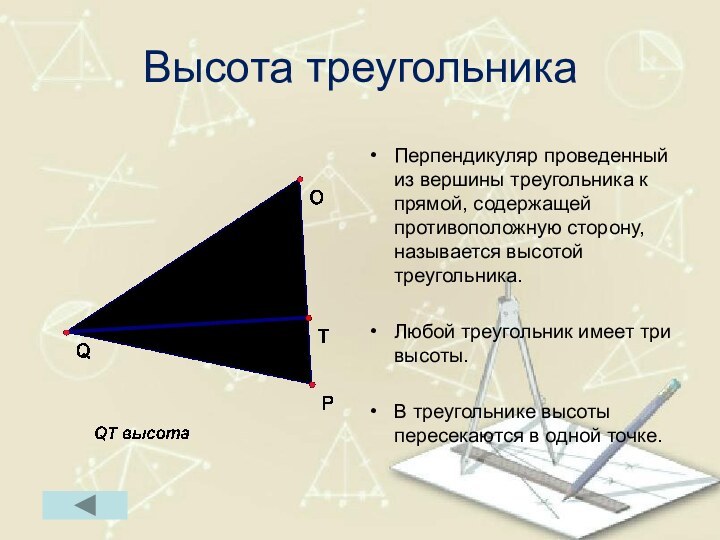
Высота треугольника
Перпендикуляр проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой треугольника.
Любой треугольник имеет три
высоты.В треугольнике высоты пересекаются в одной точке.
Слайд 25
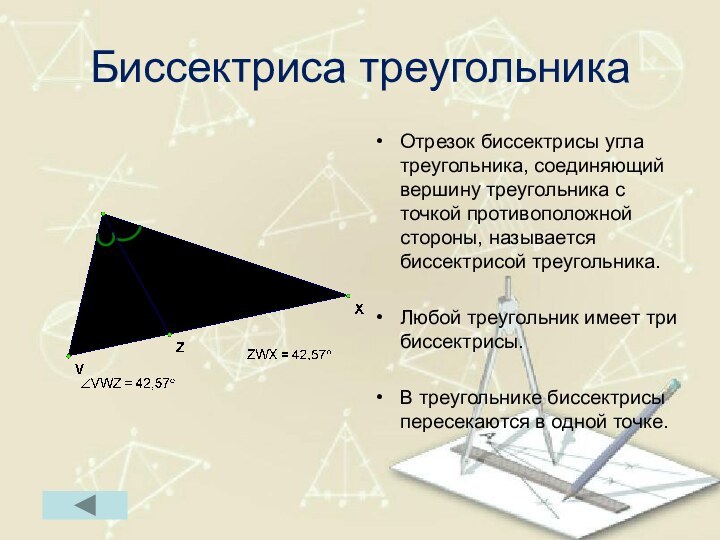
Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
с точкой противоположной стороны, называется биссектрисой треугольника.
Любой треугольник имеет
три биссектрисы.В треугольнике биссектрисы пересекаются в одной точке.
Слайд 41
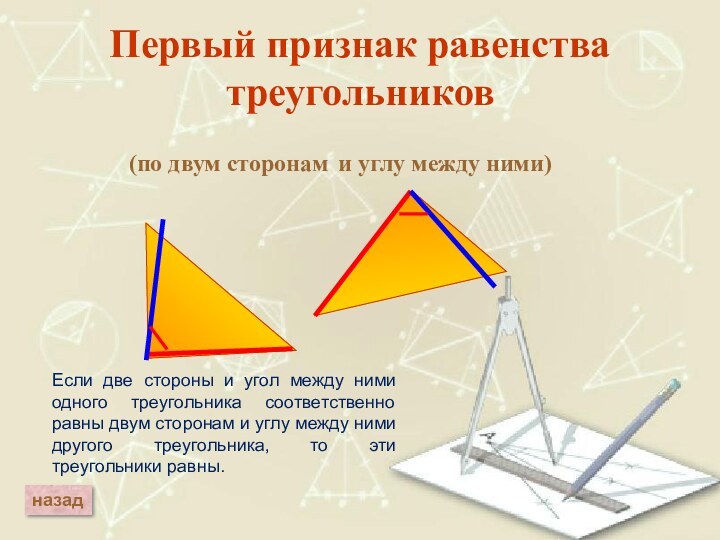
Первый признак равенства треугольников
и углу между ними)
(по двум
сторонам
назад
Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Слайд 42
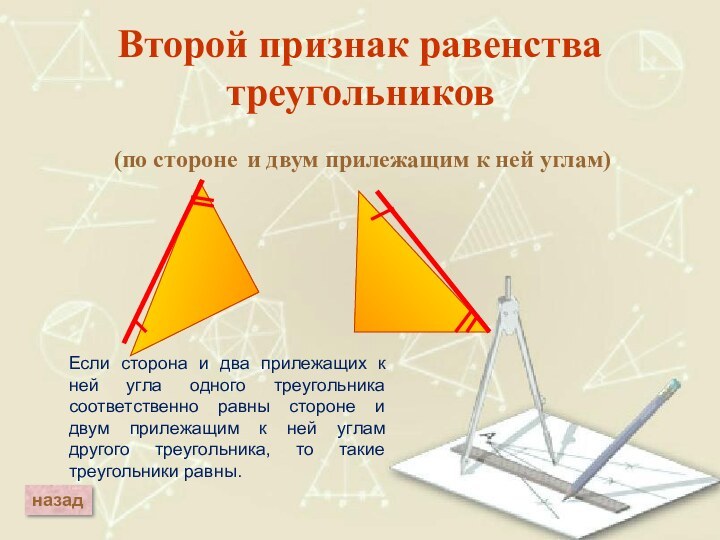
Второй признак равенства треугольников
и двум прилежащим к ней
углам)
назад
(по стороне
Если сторона и два прилежащих к ней угла
одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Слайд 43
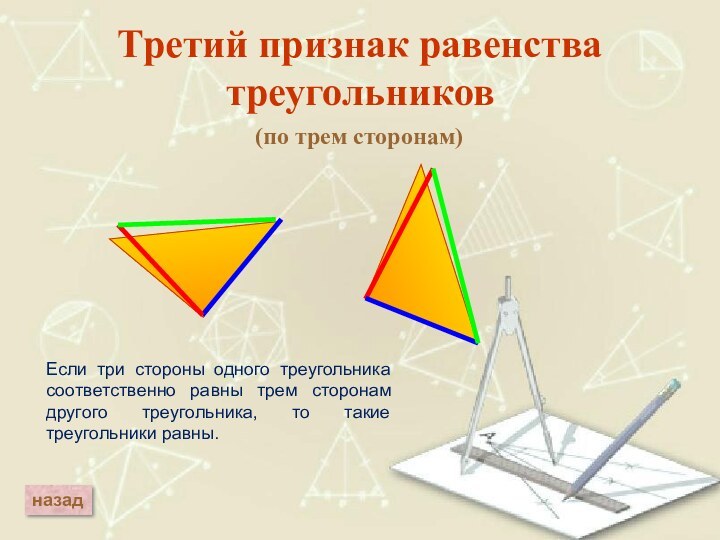
Третий признак равенства треугольников
(по трем сторонам)
назад
Если три стороны
одного треугольника соответственно равны трем сторонам другого треугольника, то
такие треугольники равны.
Слайд 46
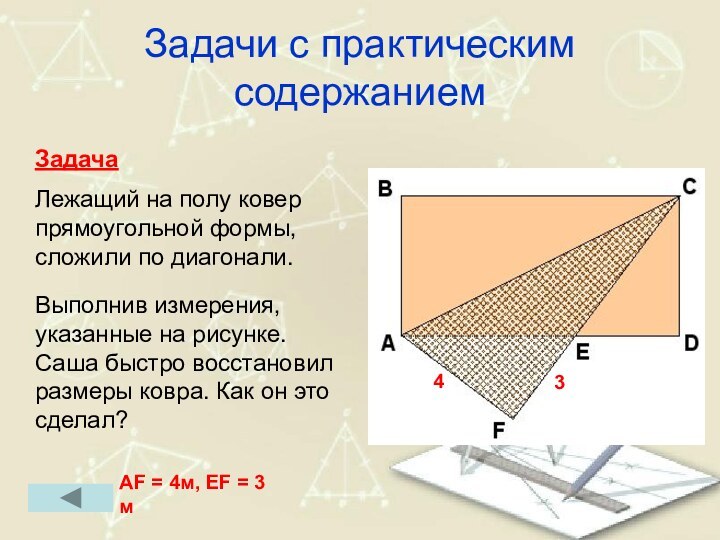
Задачи с практическим содержанием
Задача
Лежащий на полу ковер
прямоугольной формы, сложили по диагонали.
Выполнив измерения,
указанные на
рисунке. Саша быстро восстановил
размеры ковра. Как он это сделал?
4
3
AF = 4м, EF = 3 м
Слайд 47
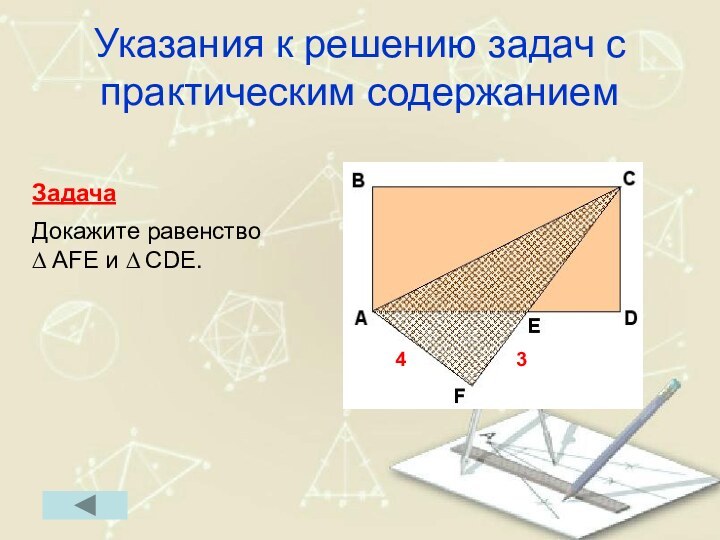
Указания к решению задач с практическим содержанием
Задача
Докажите
равенство
∆ AFE и ∆ CDE.
4
3
Слайд 48
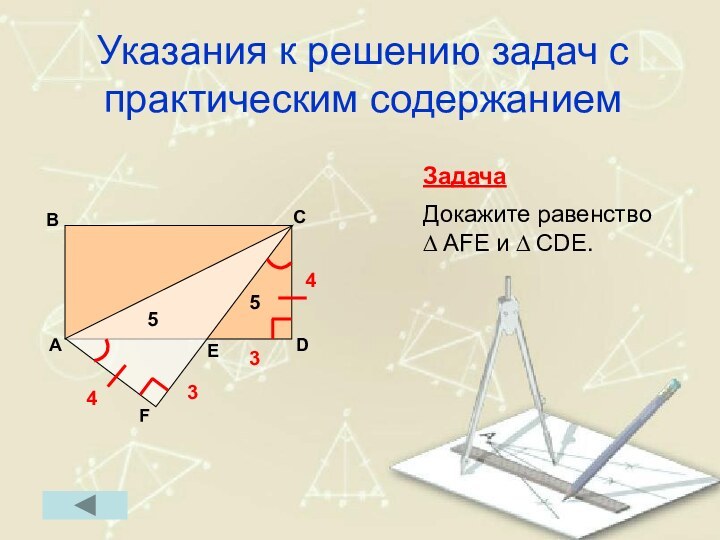
Указания к решению задач с практическим содержанием
Задача
Докажите
равенство
∆ AFE и ∆ CDE.
4
3
3
4
5
5
Слайд 49
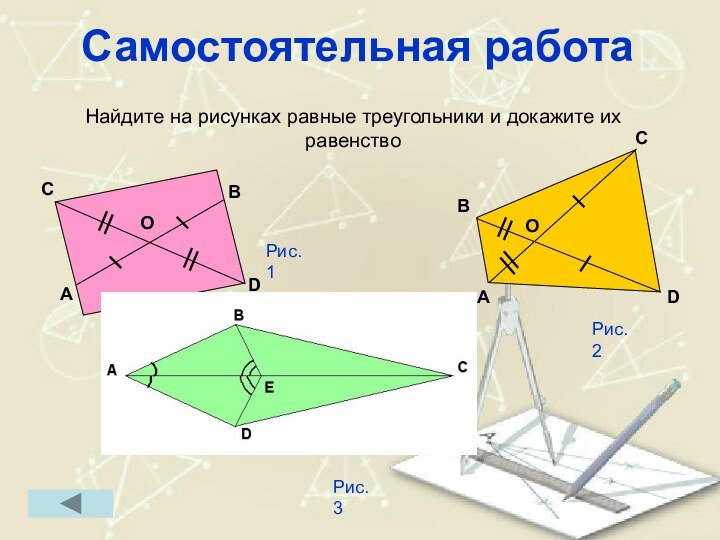
Самостоятельная работа
Найдите на рисунках равные треугольники и докажите
их равенство
Рис.1
Рис.2
Рис.3
Слайд 51
Признаки равенства прямоугольных треугольников
1
признак. По двум катетам
Прямоугольный треугольник
Слайд 52
Признаки равенства прямоугольных треугольников
2 признак. По катету
и гипотенузе
Прямоугольный треугольник
Слайд 53
Признаки равенства прямоугольных треугольников
3 признак. По катету и
прилежащему острому углу
Прямоугольный треугольник
Слайд 54
Признаки равенства прямоугольных треугольников
4
признак. По гипотенузе и острому углу
Прямоугольный треугольник
Слайд 56
Первый признак подобия треугольников
(по двум углам)
назад
Если два угла
одного треугольника соответственно равны двум углам другого, то такие
треугольники подобны.
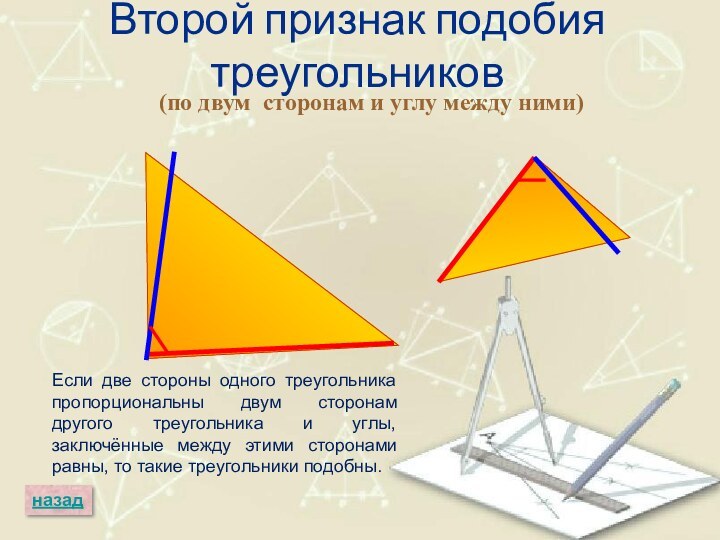
Слайд 57
Второй признак подобия треугольников
(по двум сторонам и углу
между ними)
назад
Если две стороны одного треугольника пропорциональны двум сторонам
другого треугольника и углы, заключённые между этими сторонами равны, то такие треугольники подобны.
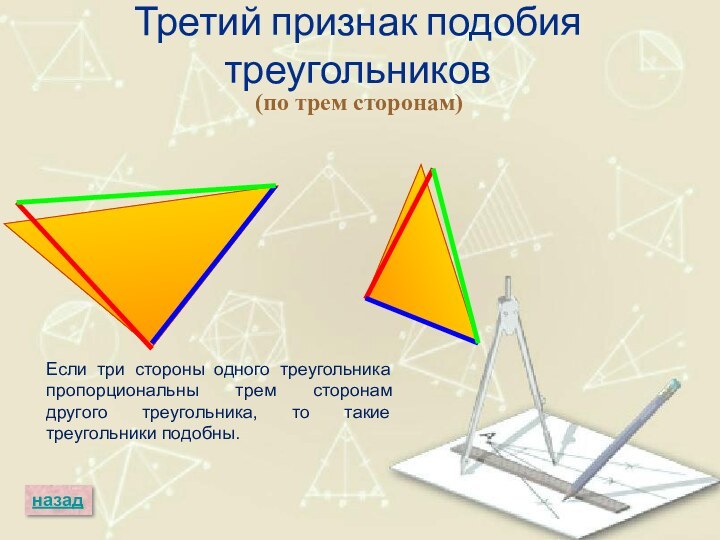
Слайд 58
Третий признак подобия треугольников
(по трем сторонам)
назад
Если три стороны
одного треугольника пропорциональны трем сторонам другого треугольника, то такие
треугольники подобны.
Слайд 59
Четырехугольник
Четырехугольник – фигура, состоящая
из четырех точек и четырех последовательно соединяющих их отрезков.
При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки – пересекаться.
Слайд 60
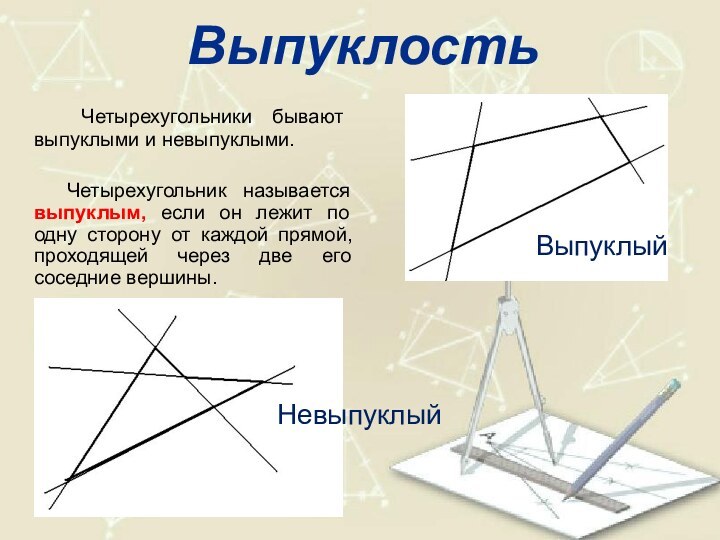
Выпуклость
Четырехугольники бывают выпуклыми и невыпуклыми.
Четырехугольник называется выпуклым, если он лежит по одну
сторону от каждой прямой, проходящей через две его соседние вершины.Выпуклый
Невыпуклый
Слайд 62
Площади плоских фигур:
Определение площади
Свойства площадей
Формулы площадей четырёхугольников
Закрепление материала
Начало
Слайд 63
Параллелограмм
Определение:
Параллелограмм – четырехугольник, у
которого противолежащие стороны параллельны.
Свойства параллелограмма
Слайд 64
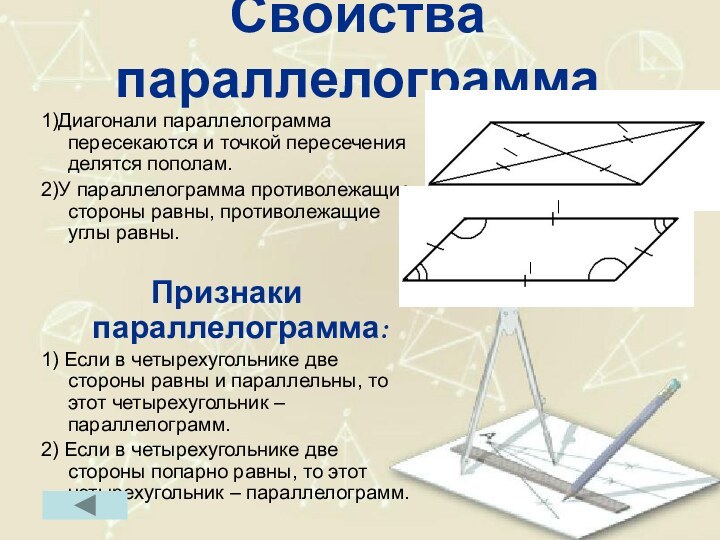
Свойства параллелограмма
1)Диагонали параллелограмма пересекаются и точкой пересечения делятся
пополам.
2)У параллелограмма противолежащие стороны равны, противолежащие углы равны.
Признаки параллелограмма:
1)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм. 2) Если в четырехугольнике две стороны попарно равны, то этот четырехугольник – параллелограмм.
Слайд 65
Прямоугольник
Определение:
Прямоугольник – это параллелограмм,
у которого все углы прямые.
Свойства
прямоугольника
Слайд 66
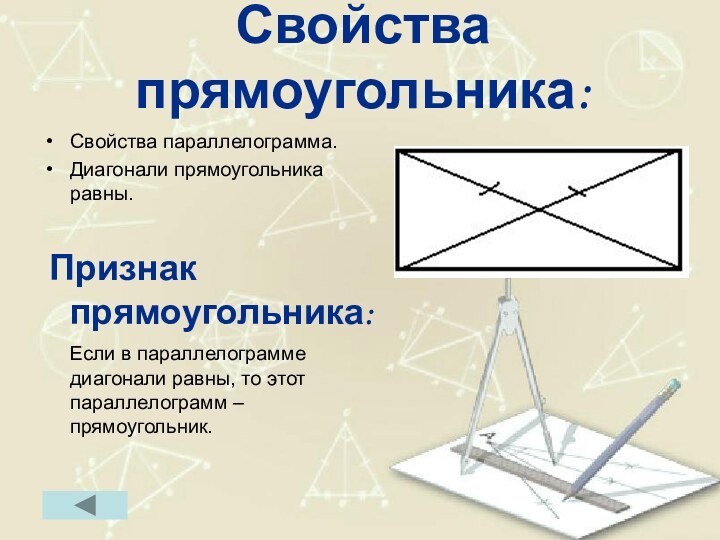
Свойства прямоугольника:
Свойства параллелограмма.
Диагонали прямоугольника равны.
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм –
прямоугольник.
Слайд 68
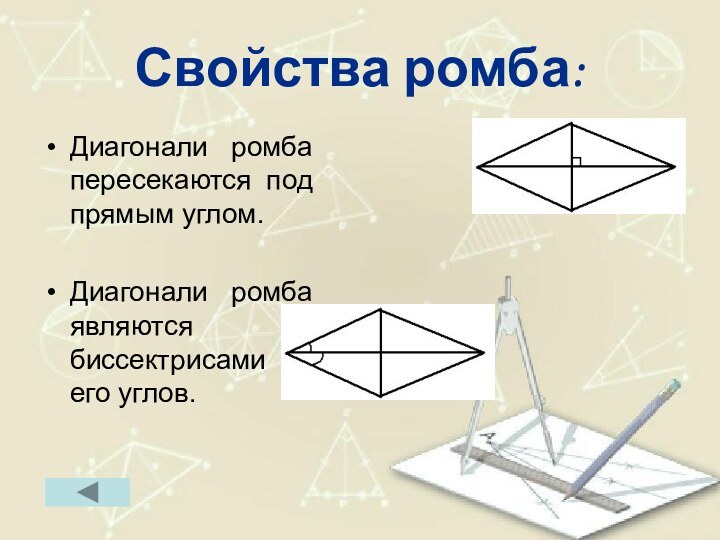
Свойства ромба:
Диагонали ромба пересекаются под прямым углом.
Диагонали
ромба являются биссектрисами его углов.
Слайд 69
Квадрат
Определение:
1)Квадрат – это прямоугольник, у которого все
стороны равны.
2)Квадрат – это ромб, у которого все углы
прямые.Свойства квадрата
Слайд 70
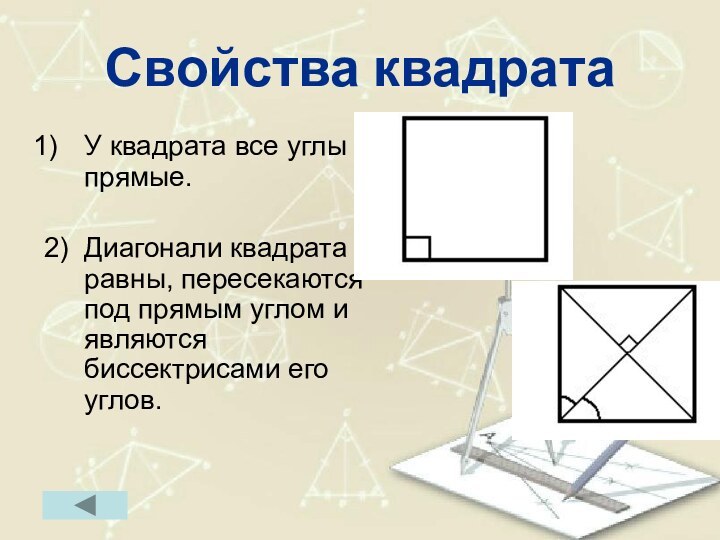
Свойства квадрата
У квадрата все углы прямые.
2) Диагонали квадрата
равны, пересекаются под прямым углом и являются биссектрисами его
углов.
Слайд 71
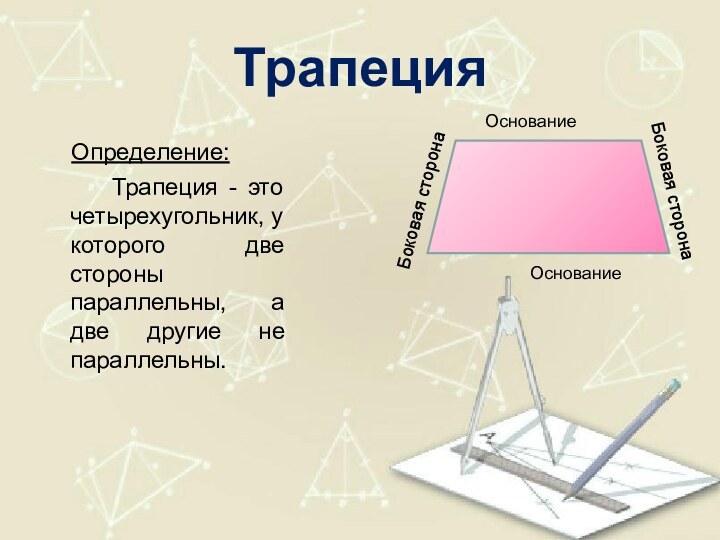
Трапеция
Определение:
Трапеция - это четырехугольник,
у которого две стороны параллельны, а две другие не
параллельны.Основание
Основание
Боковая сторона
Боковая сторона
Слайд 73
Понятие площади
Что принимают за единицу измерения площади?
В
каких единицах измеряется площадь?
Чем выражается площадь многоугольника, что показывает
это число?
Слайд 74
Свойства площадей
Равные многоугольники имеют равные площади
Если многоугольник составлен
из нескольких многоугольников, то его площадь равна сумме площадей
этих многоугольниковПлощадь квадрата равна квадрату его стороны
Начало





























