степени (n), в которую надо возвести a, чтобы получить
b (an =b)logab
(произносится: логарифм числа b по основанию a)
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре 10 Логарифмы
Содержание
- 3. ЛогарифмЛогарифмом числа b по основанию a называется
- 4. Свойства логарифмов
- 5. Свойства логарифмов
- 6. Свойства логарифмов
- 7. Виды логарифмических уравнений
- 8. 1.Решение логарифмических уравнений на основании определения логарифма ОДЗ: 2x+1>0x>-1/2 Ответ: 4
- 9. 2.Метод потенцирования Проверка:-- не существует-- не
- 10. 3. Приведение логарифмическогоуравнения к квадратномуОДЗ:x>0 Ответ: 0,001; 10
- 11. 4.Уравнения, решаемые приведением логарифмов к одному и тому же основанию ОДЗ:x>0 Ответ: 3
- 12. 5. Уравнения, решаемые логарифмированием его обеих частейЛогарифмируя обе части уравнения получим:Пусть тогдаОДЗ:x>0 Ответ: 0,001; 10
- 13. Заполни пропускиLog? b + Logx ? =
- 14. ВычислиLg 2 + lg 5Log3 3 – 0,5 log3 9Log 2Log4 16 + log3 27
- 15. Логарифмическая функция и её график:y 1
- 16. Найти график функции y = log2 x yyyyxxxx 0 0 0 0
- 17. Найти график функции y = lgx
- 18. График какой функции изображен на рисунке?
- 19. График какой функции изображен на рисунке?
- 20. Логарифмические неравенства
- 21. Логарифмическим неравенством называют неравенства вида logaf(x)>logag(x), где
- 22. log3 (2х-4)>log3(14-x)Ответ: 6log (2х-4)>log (14-x)Ответ: 2
- 23. Решить неравенство:log2(x-3) + log2(x-2) ≤ 1Решение:О.Д.З. X>3.
- 24. Скачать презентацию
- 25. Похожие презентации
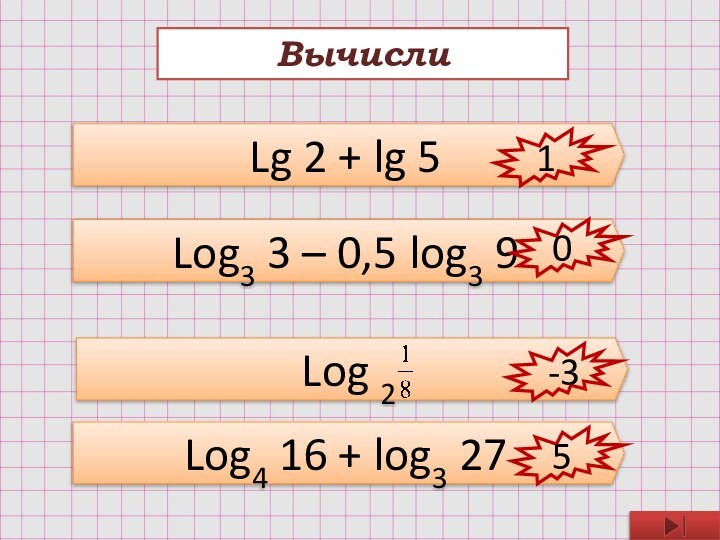
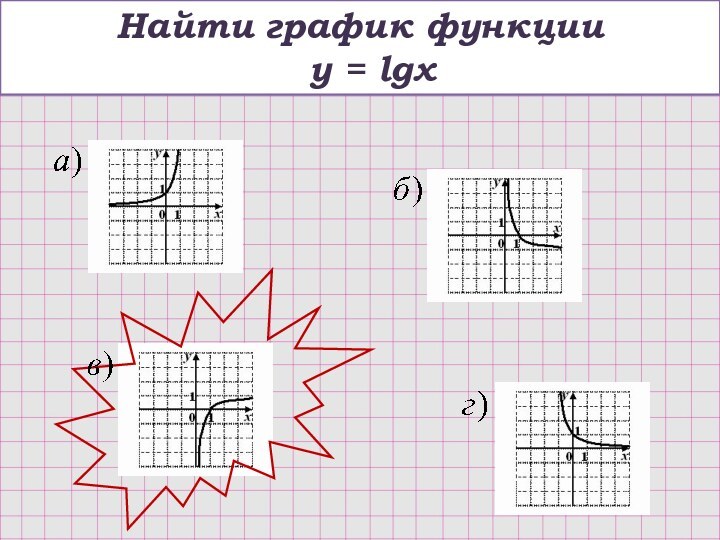
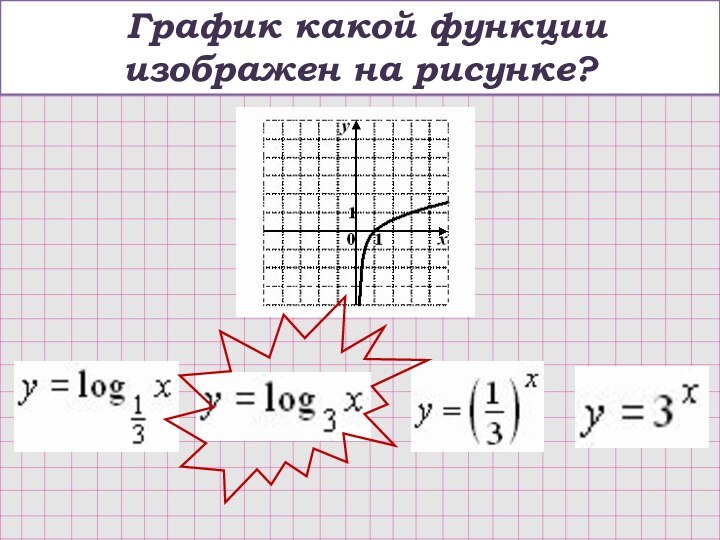
ЛогарифмЛогарифмом числа b по основанию a называется показатель степени (n), в которую надо возвести a, чтобы получить b (an =b)logab(произносится: логарифм числа b по основанию a)
Слайд 3
Логарифм
Логарифмом числа b по основанию a называется показатель
Слайд 8
1.Решение логарифмических уравнений на основании определения логарифма
ОДЗ:
2x+1>0
x>-1/2
Ответ: 4
Слайд 9
2.Метод потенцирования
Проверка:
-- не существует
-- не имеет смысла
-- не
существует
-- не имеет смысла
Ответ: корней нет
Слайд 12
5. Уравнения, решаемые логарифмированием его обеих частей
Логарифмируя обе
части уравнения получим:
Пусть
тогда
ОДЗ:
x>0
Ответ:
0,001; 10
Слайд 13
Заполни пропуски
Log? b + Logx ? = Log?
(?a)
Logx ? - Log? b = Log? (a/?)
Logx b?
= pLog? (?)х
а
х
b
а
х
х
b
p
х
b
Слайд 15
Логарифмическая функция
и её график:
y
1
a
1
-
1/a
1
x
y=logax, a>1
1
a
1/a
1
-
1
x
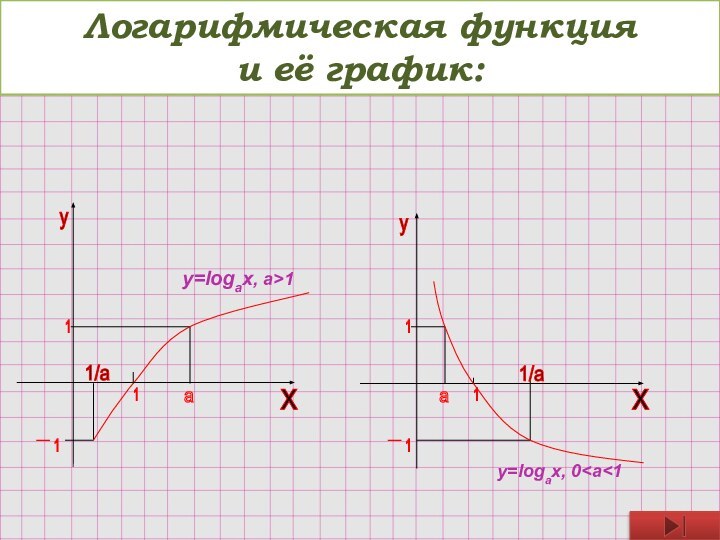
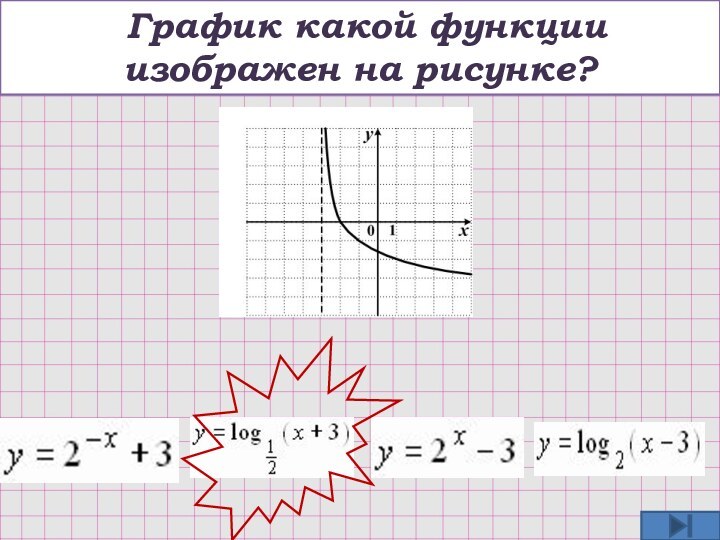
y=logax, 0 y
Слайд 21
Логарифмическим неравенством называют неравенства вида
logaf(x)>logag(x),
где
а - положительное число, отличное от 1.
При а>1 logaf(x)>logag(x)
<=> f(x)>0, g(x) >0, f(x)>g(x)
При 0 < а < 1 logaf(x)>logag(x)
<=> f(x)>0, g(x) >0, f(x) < g(x)
Слайд 23
Решить неравенство:
log2(x-3) + log2(x-2) ≤ 1
Решение:
О.Д.З. X>3.
Используя
свойства логарифма, получаем:
log2(x-3)(x-2) ≤ log22.
Логарифмическая функция с основанием
2 является возрастающей (т.к. 2>1), поэтому при x>3 неравенство log2(x-3) (x-2) ≤ log22 выполняется при (x-3)(x-2)≤2. Это неравенство можно записать в виде системы уравнений:(x-3)(x-2) ≤2
X>3
/////////////// ///////
0 1 3 4
Ответ: 3
XXXX
x
