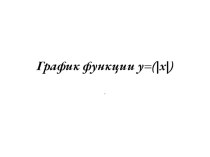- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вычисление площадей плоских фигур
Содержание
- 2. Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a0bxy=f(x)y
- 3. y=f(x) непрерывная f(x)≤0 на [a; b] a0by=f(x)yxНайти площадь фигуры
- 4. 0yxy=g (x)y=f (x)bay = f (x), y
- 5. y=f (x)ay=g (x)b0yxНайти площадь фигурыy = f
- 6. cxy=f (x)ay=g (x)b0yНайти площадь фигуры y =
- 7. cxy=f (x)ay=g (x)b0yНайти площадь фигуры
- 8. cxy=f (x)ay=g (x)b0yНайти площадь фигуры
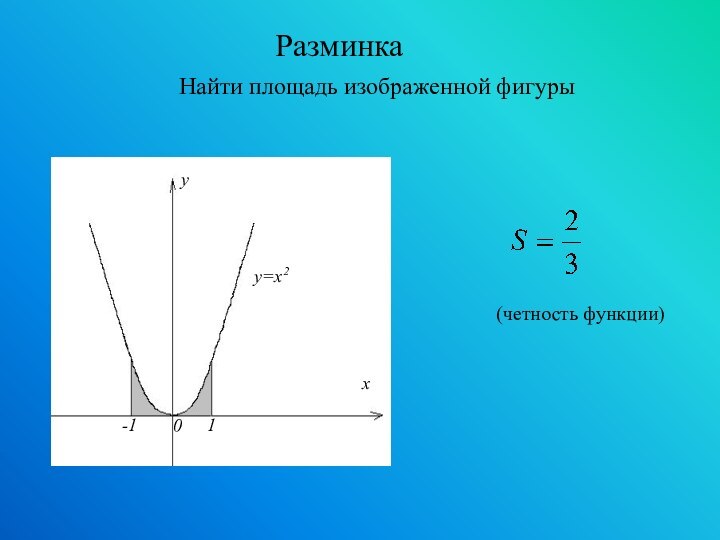
- 9. (четность функции)Разминка Найти площадь изображенной фигуры
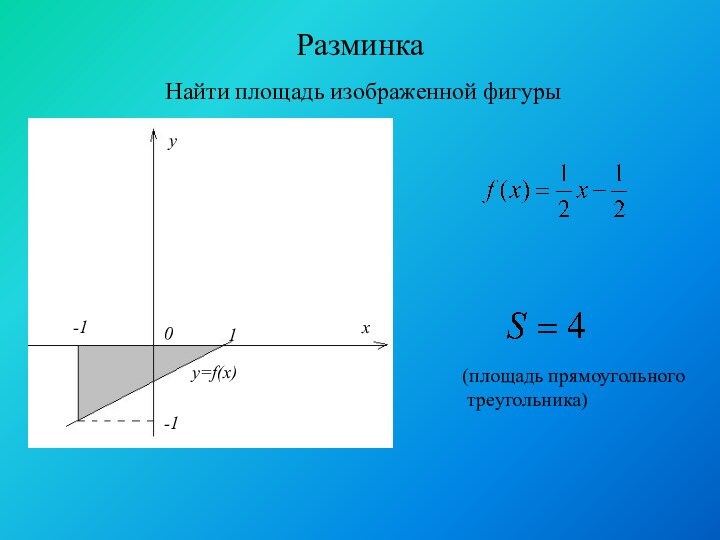
- 10. Разминка Найти площадь изображенной фигуры(площадь прямоугольного треугольника)
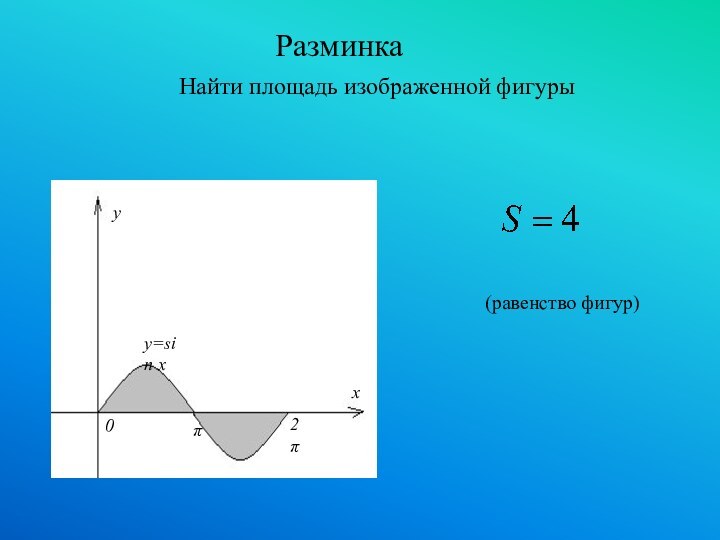
- 11. Разминка Найти площадь изображенной фигуры(равенство фигур)
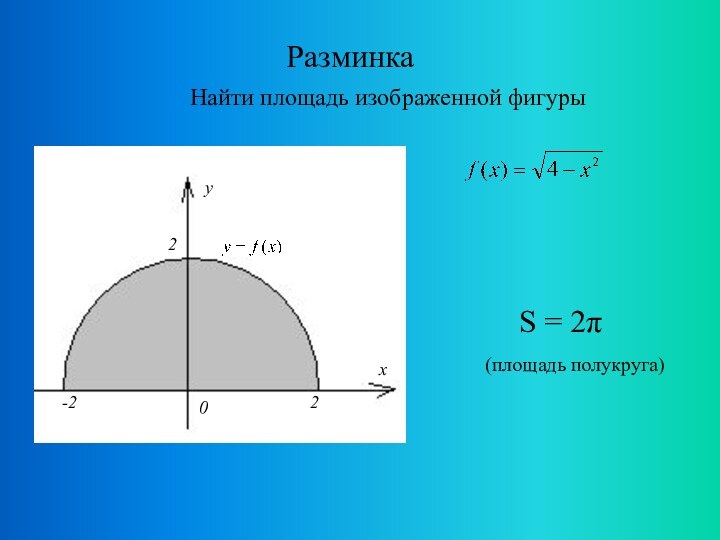
- 12. Разминка Найти площадь изображенной фигурыS = 2π(площадь полукруга)
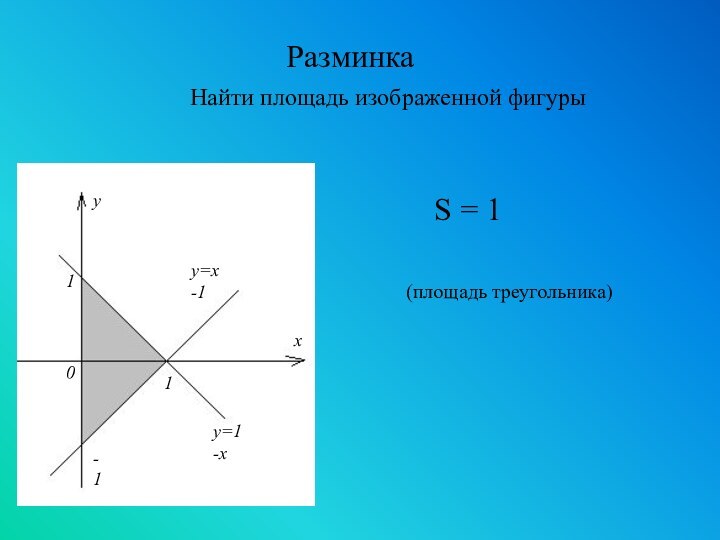
- 13. Разминка Найти площадь изображенной фигурыS = 1(площадь треугольника)
- 14. Задачи1) Найти площадь фигуры, ограниченной линиями
- 15. 1 способ S
- 16. 2) Фигура, ограниченная линиями y=x+6,
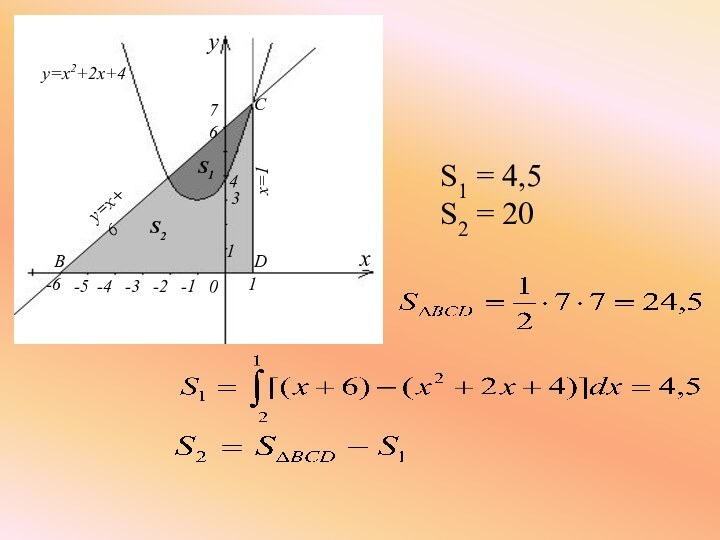
- 17. S1 = 4,5 S2 = 201
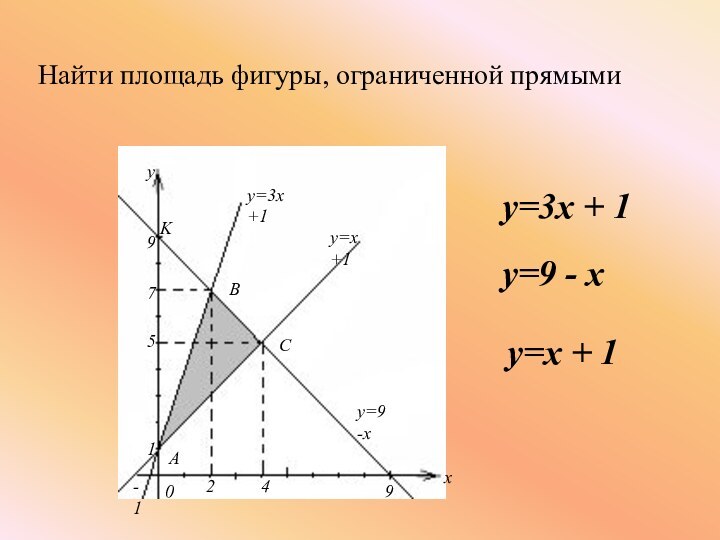
- 18. Найти площадь фигуры, ограниченной прямыми
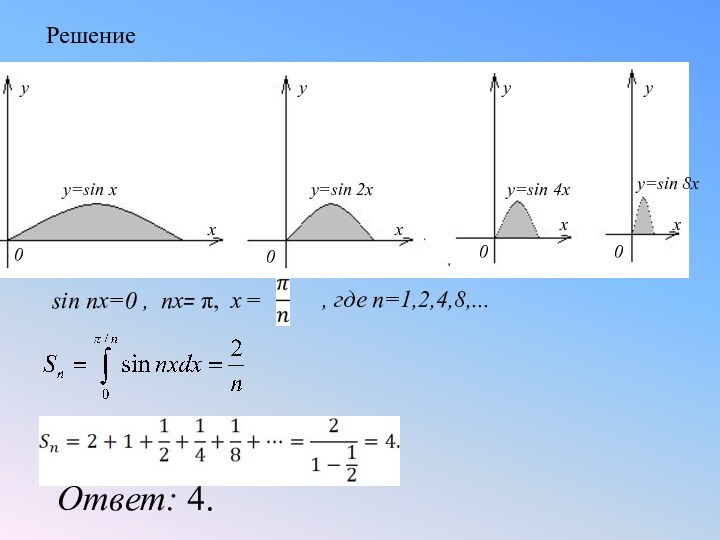
- 19. Интересные задачи1. Найти сумму площадей бесконечного количества
- 20. Ответ: 4., где n=1,2,4,8,...sin nx=0 , nx= π, x = Решение
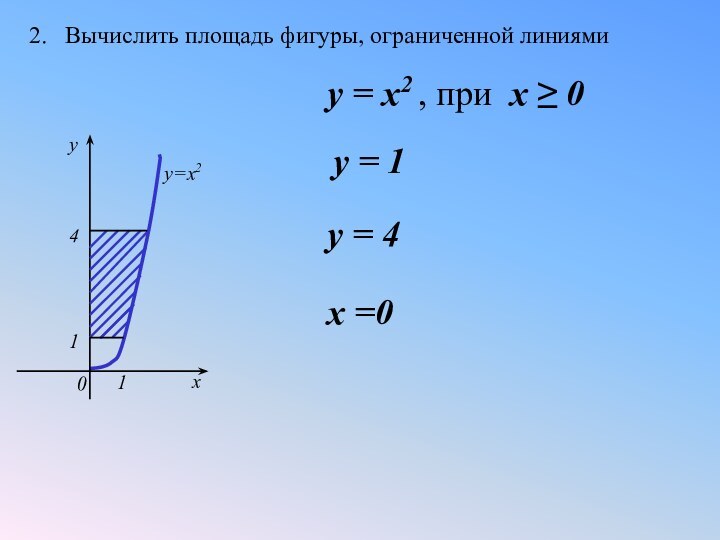
- 21. 2. Вычислить площадь фигуры, ограниченной линиями
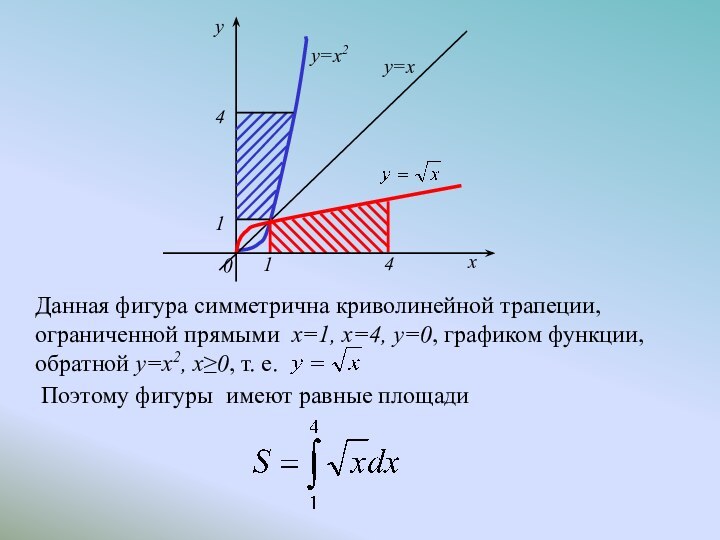
- 22. Данная фигура симметрична криволинейной трапеции,ограниченной прямыми x=1,
- 23. Если фигура ограничена линиями x=ϕ1(y), x=ϕ2(y), y=c; y=d, где c
- 24. Скачать презентацию
- 25. Похожие презентации

![Вычисление площадей плоских фигур Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a0bxy=f(x)y](/img/tmb/12/1196152/50b66b0c9320ebcd6c4d036b2fa63333-720x.jpg)
![Вычисление площадей плоских фигур y=f(x) непрерывная f(x)≤0 на [a; b] a0by=f(x)yxНайти площадь фигуры](/img/tmb/12/1196152/2b004a4281ab005f2204fe5ec91d2a3e-720x.jpg)
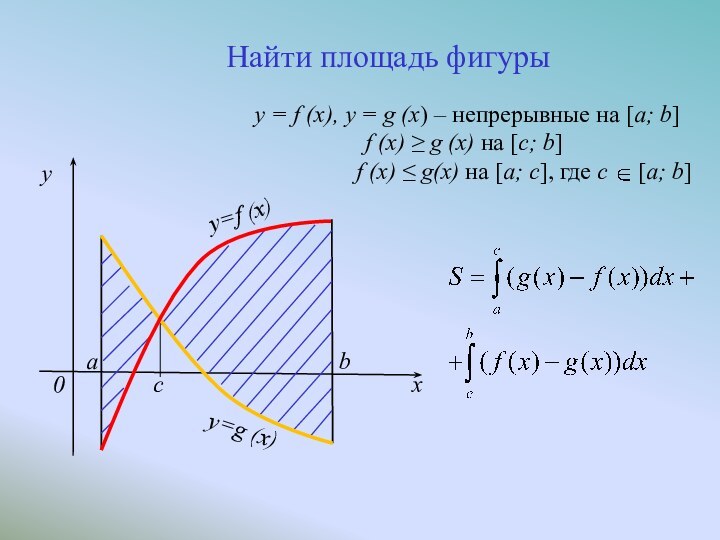




Слайд 4
0
y
x
y=g (x)
y=f (x)
b
a
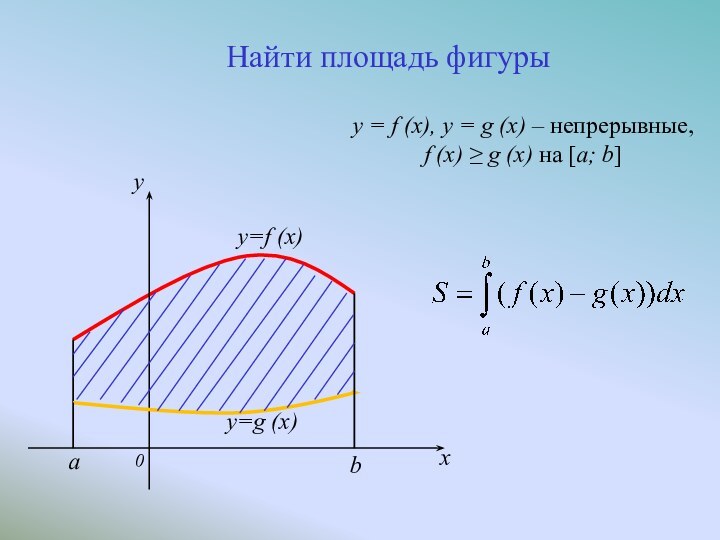
y = f (x), y =
g (x) – непрерывные,
f (x) ≥ g (x) на
[a; b]Найти площадь фигуры
Слайд 5
y=f (x)
a
y=g (x)
b
0
y
x
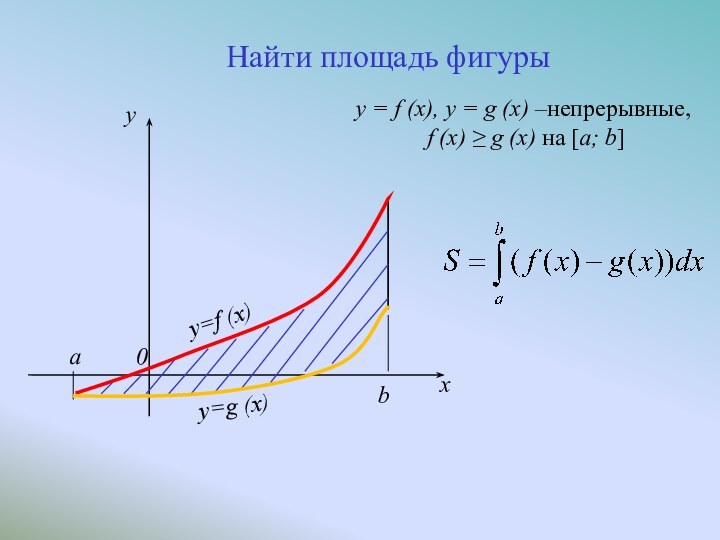
Найти площадь фигуры
y = f (x),
y = g (x) –непрерывные,
f (x) ≥
g (x) на [a; b]
Слайд 6
c
x
y=f (x)
a
y=g (x)
b
0
y
Найти площадь фигуры
y = f
(x), y = g (x) – непрерывные на [a;
b]f (x) ≥ g (x) на [c; b]
f (x) ≤ g(x) на [a; c], где с [a; b]
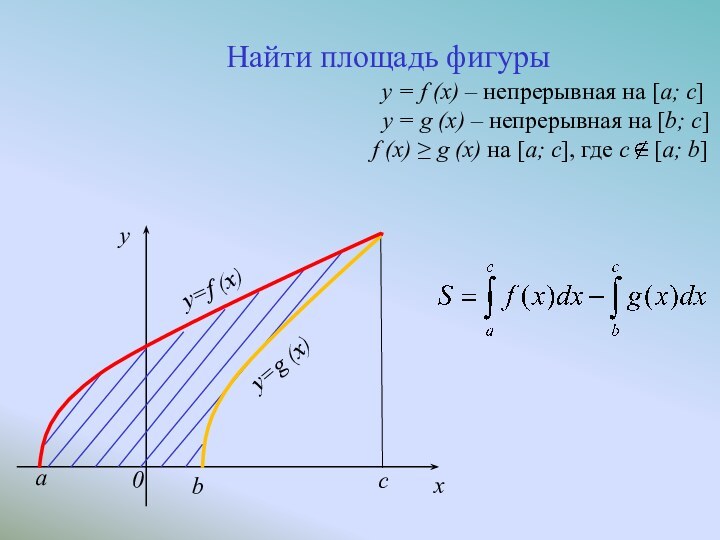
Слайд 7
c
x
y=f (x)
a
y=g (x)
b
0
y
Найти площадь фигуры
y = f (x) – непрерывная на [a; c]
y = g (x) – непрерывная на [b; c]
f (x) ≥ g (x) на [a; c], где с [a; b]
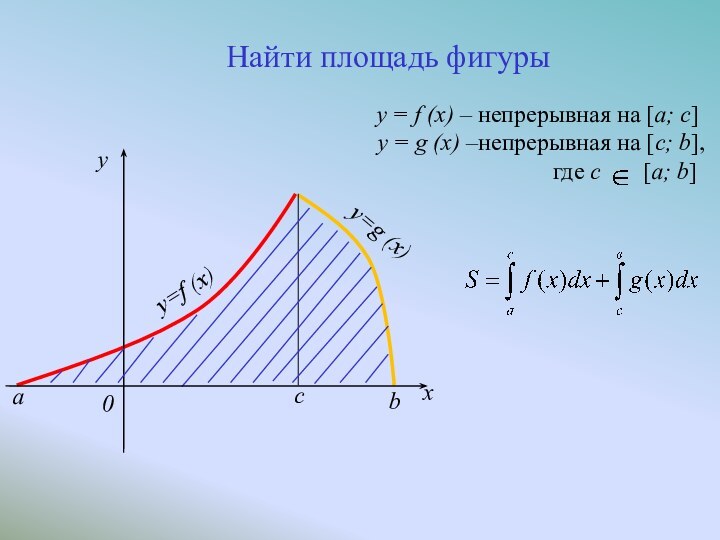
Слайд 8
c
x
y=f (x)
a
y=g (x)
b
0
y
Найти площадь фигуры
y = f (x) – непрерывная на [a; c]
y = g (x) –непрерывная на [c; b],
где с [a; b]
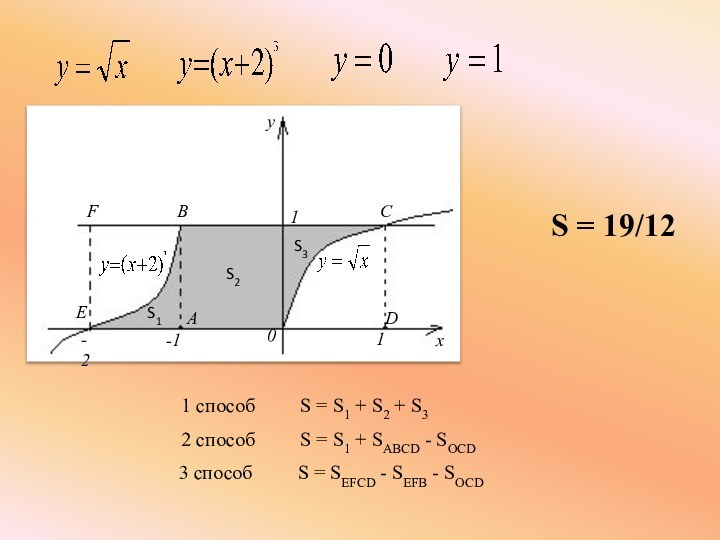
Слайд 15
1 способ S =
S1 + S2 + S3
S = 19/12
2 способ
S = S1 + SABCD - SOCD
3 способ S = SEFCD - SEFB - SOCD
S1
S2
S3
Слайд 16
2) Фигура, ограниченная линиями
y=x+6,
x=1,
y=0, делится параболой
y=x2 + 2x + 4
на две части.
Найти площадь каждой части.
Слайд 19
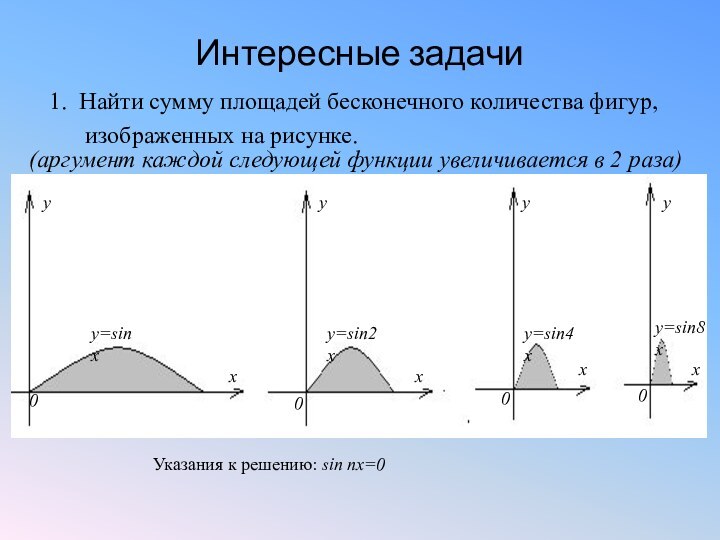
Интересные задачи
1. Найти сумму площадей бесконечного количества фигур,
изображенных на рисунке.
(аргумент каждой следующей
функции увеличивается в 2 раза)Указания к решению: sin nx=0
Слайд 21
2. Вычислить площадь фигуры, ограниченной линиями
1
1
4
0
x
y
y=x2
y = 1
y = 4
x =0
у = x2 , при x ≥ 0
Слайд 22
Данная фигура симметрична криволинейной трапеции,
ограниченной прямыми x=1, x=4,
y=0, графиком функции, обратной y=x2, x≥0, т. е.
Поэтому
фигуры1
4
1
4
0
x
y
y=x
y=x2
имеют равные площади
Слайд 23
Если фигура ограничена линиями
x=ϕ1(y), x=ϕ2(y), y=c; y=d,
где c
площадь может быть вычислена по формуле