Презентация на тему по математике на тему Графики функций, содержащих модуль (9 класс)

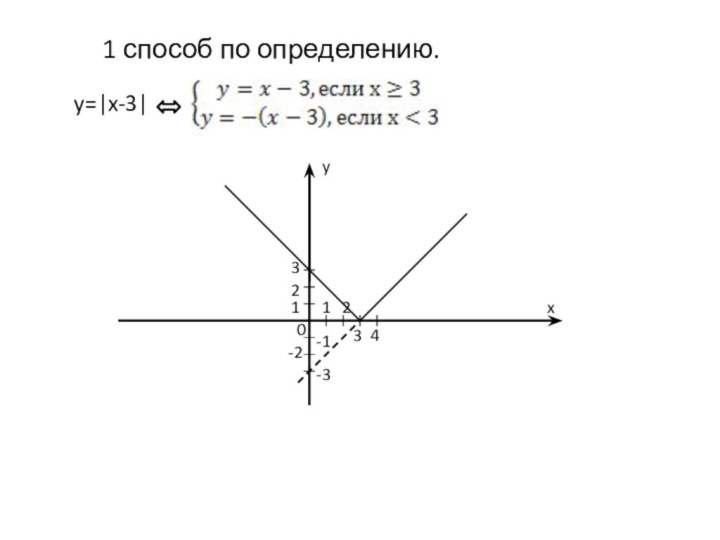
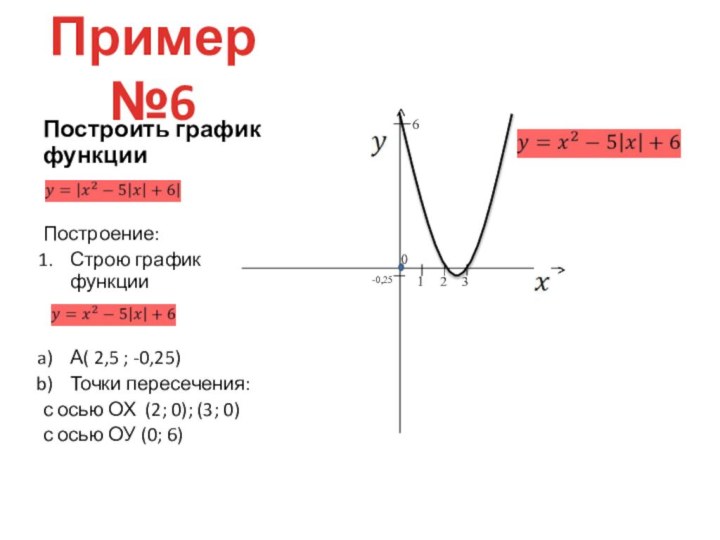
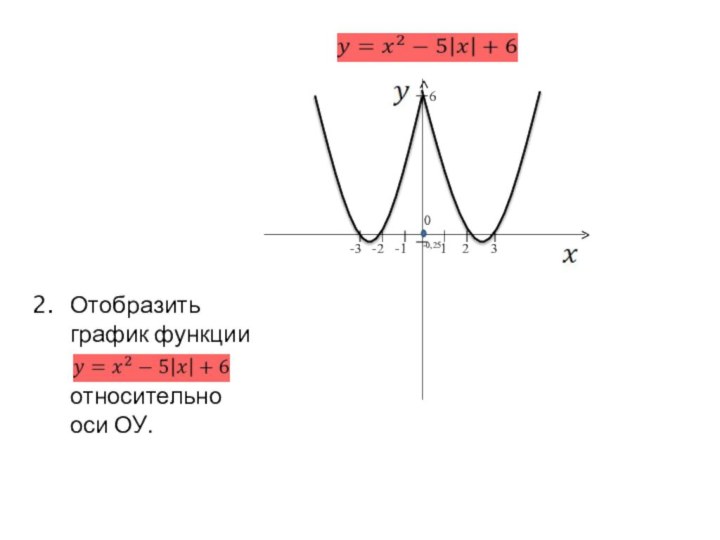
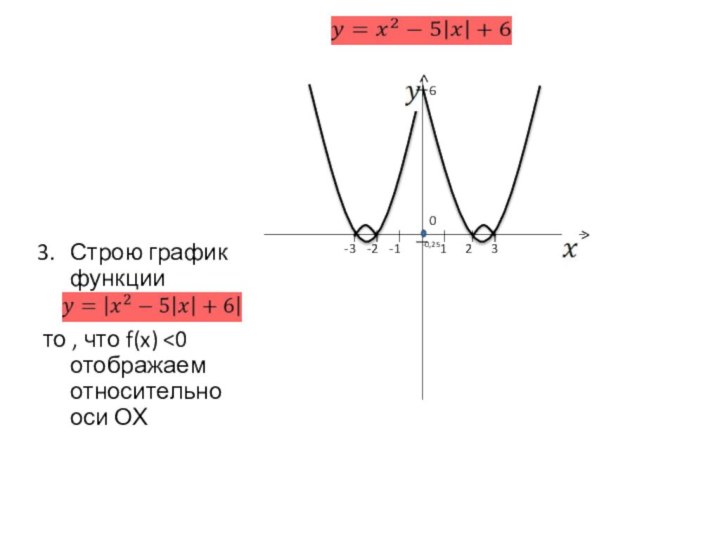
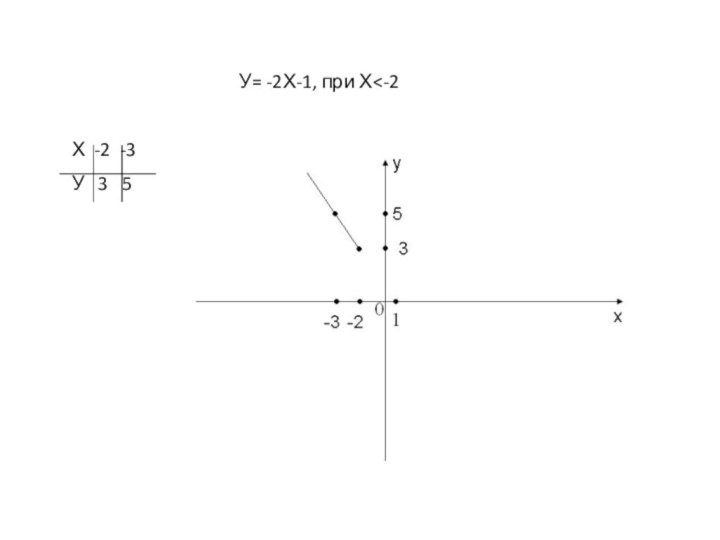
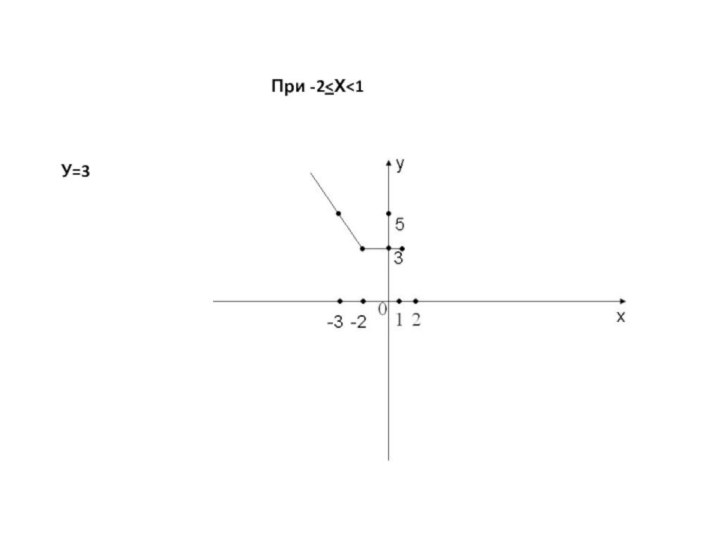
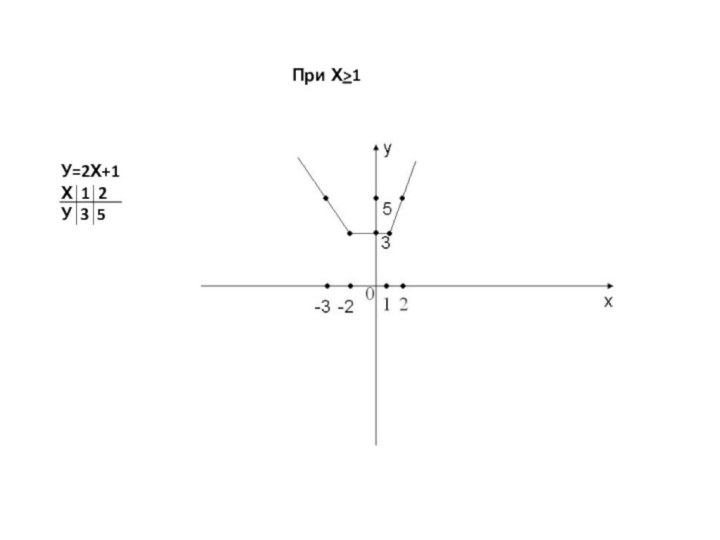
двух графиков: у = f(х) – в правой полуплоскости

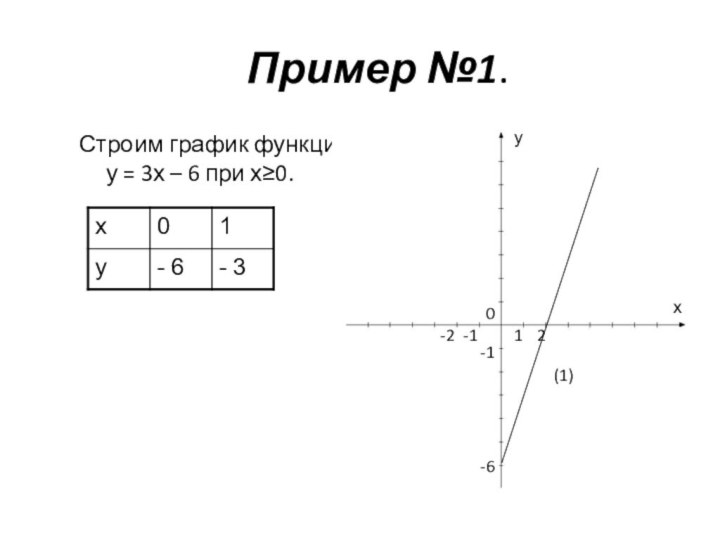
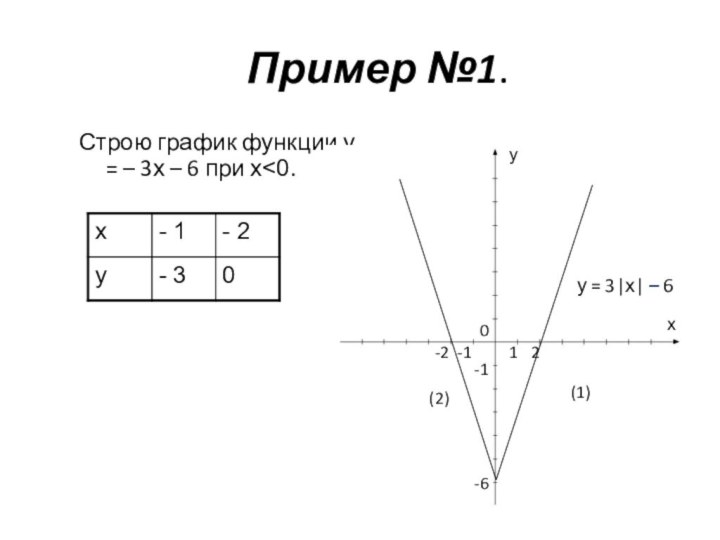
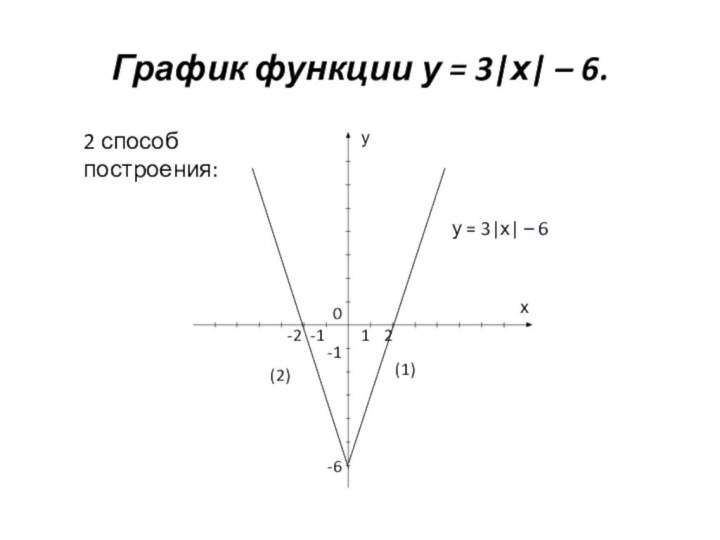
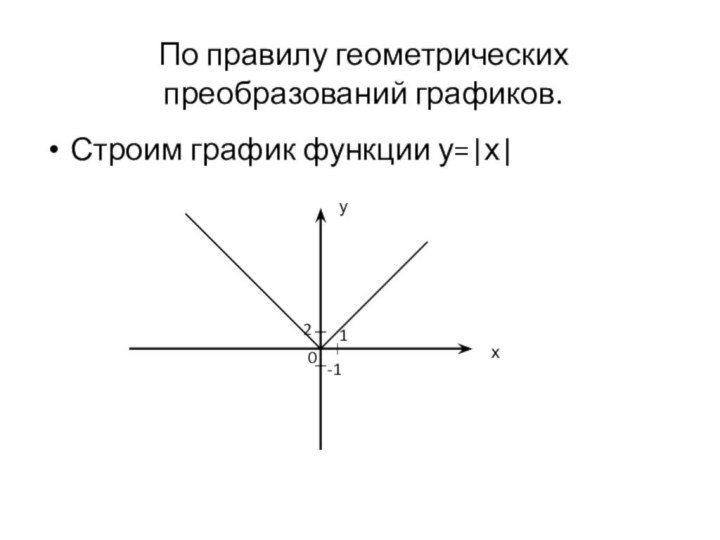
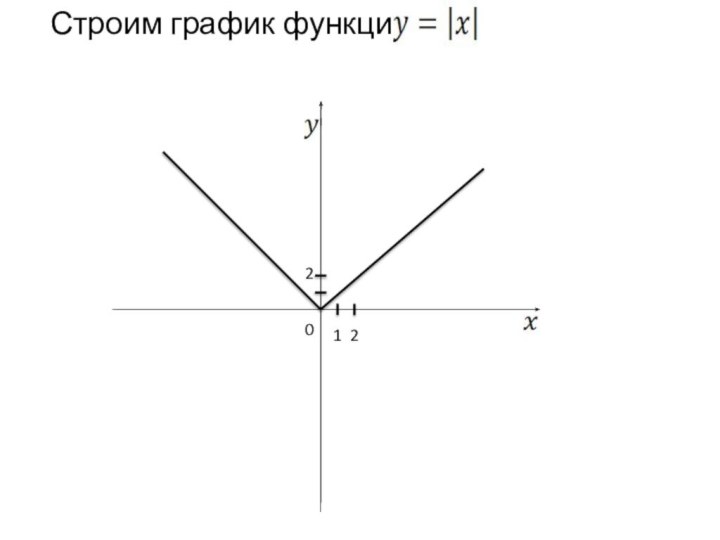
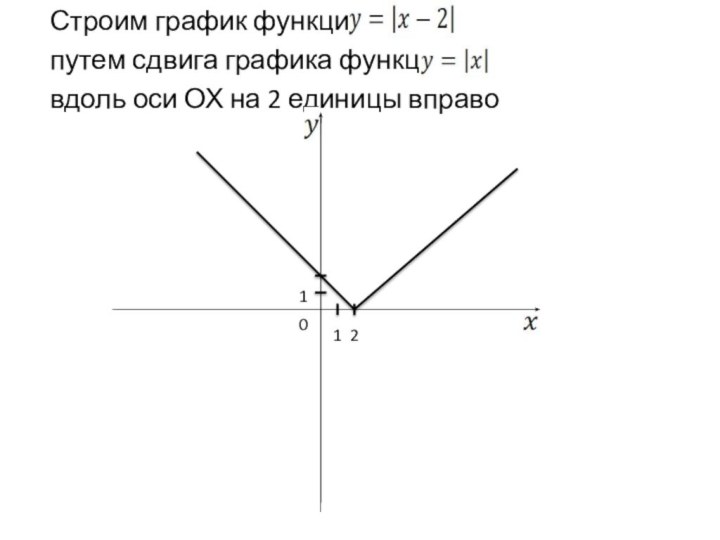
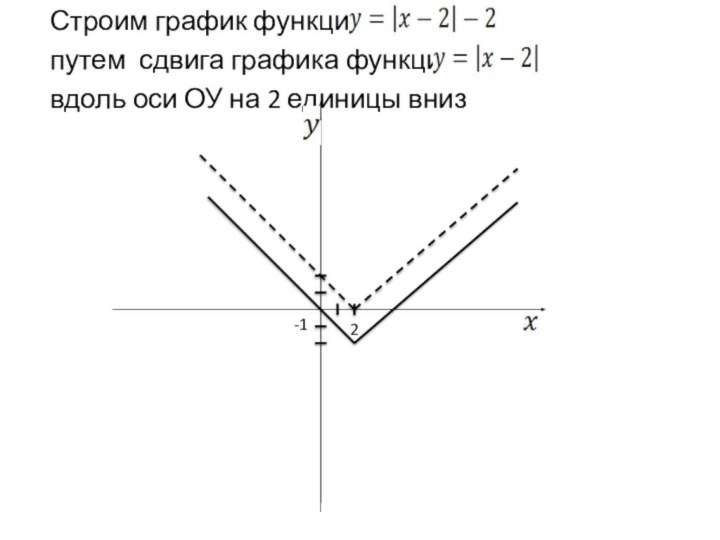
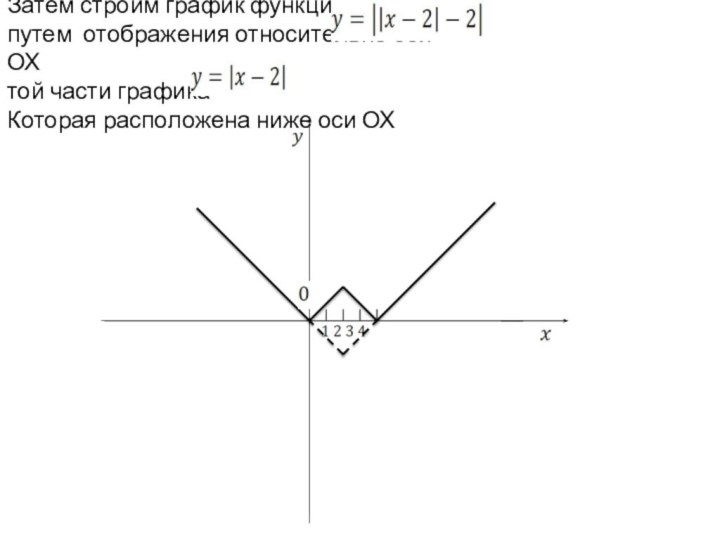
и у = f(-х) – в левой полуплоскости. График функции у = f(|x|) получается из графика функции у = f(х) следующим образом: при х≥0 график сохраняется, а при х<0 отражает построенную часть симметрично относительно оси Оу.

Построение графика функции y=(|x|)

6.
Построение.

6 при х≥0.

(1)

– 6 при х

– 6 для х>0.
Достраиваем его левую часть для

х<0, симметрично построенной относительно оси Оу.

Построить график функции у = 3|х| – 6.
Построение.

3|х| – 6
2 способ построения:

у = f(|х|), где f(х) = х² –

2х – 3. График функции f(х) = x² – 2x – 3 есть парабола с вершиной в точке (1; –4), т.к. х² – 2х – 3 = (х – 1)² – 4. Построим ту часть параболы у = (х – 1)² – 4, которая соответствует неотрицательным значениям аргумента. Затем достроим другую часть графика, симметричную первой относительно оси Оу. Получим график функции у = х² –2|х| – 3.

Построить график функции f(x) = x² – 2|х| – 3.
Построение.

3.
(1)
(2)
f(x) = x² – 2|x| – 3

y=f(x), лежащая над осью OX, сохраняется, а часть его,

лежащая под осью OX, отображается симметрично относительно оси OX.

1 способ по определению.

0

-1

-2

-3

1

2

3

1

2

3

4

x

y

у

х

0

-1

1

2

функции у=IхI вдоль ох на 3 единицы вправо

у
х
0
1
2
1
-1
3
2
3

Построение
1. Строим график функции y= - +

2x (ту часть графика, которая расположена ниже оси, наметим пунктиром)
2. Потом строим недостающую часть графика путем симметрии относительно оси пунктирной части
у
у=|- +2х|


0 х

1

2

3

4

-1

-2

-3

-1

-2

-3

-4

, надо сначала построить график

функции , при x>0, затем при х<0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где < 0, построить изображение, симметричное графику относительно оси ОХ.

на 2 единицы вправо
1
0
2
1

на 2 единицы вниз
-1
2

той части графика
Которая расположена ниже оси ОХ

2,5 ; -0,25)
Точки пересечения:
с осью ОХ (2; 0); (3;

0)
с осью ОУ (0; 6)

1

2

3

6

-0,25

0

> 

> 

> 

>

относительно оси ОУ.

6

-2

3

2

-0,25

0

-3

1

-1

>

>

относительно оси ОХ


-2
-3
-0,25
6
1
2
-1
3
0
>

>

такого вида наиболее распространенным является метод, при котором знак

модуля раскрывается на основании самого определения модуля.
В этом случае область допустимых значений данной функции разбивают на множества, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. На каждом таком множестве функцию записывают без знака модуля и строят график. Объединение множества решений, найденных на всех частях области допустимых значений функции, составляет множество всех точек графика заданной функции.

подмодульные выражения обращаются в нуль.
Х-1=0

Х+2=0
Х=1 Х=-2
Эти точки разбивают числовую ось на три промежутка.






При Х<-2 ; У=-2Х-1
У=|Х-1|+|Х+2|= При -2<Х<1 ; У=3
При Х>1 ; У=2Х+1

-2

1

У= -2Х-1, при Х<-2

Х -2 -3
У 3 5

При -2<Х<1

У=3